Под обратными задачами спектрального анализа понимают задачи восстановления оператора по его заданным спектральным характеристикам, к которым можно отнести спектры, спектральную функцию, данные рассеяния. Подобным вопросам для различных операторов посвящен ряд работ таких известных математиков как В. А. Амбарцумян, В. А. Марченко, А. И. Прилепко, В. А. Садовничий, В. А. Юрко и др. [1, 8, 10] Наиболее исследована обратная задача для оператора Штурма – Лиувилля [6]. Впервые обратная задача для оператора Лапласа с потенциалом была поставлена Ю. М. Березанским [1].
Среди публикаций, относящихся к обратным задачам спектрального анализа для операторов с дискретным спектром, можно отметить работы Академика РАН В. А. Садовничего, В. В. Дубровского и их учеников [2–4, 7–9]. В настоящей работе получен результат для степени возмущенного оператора Лапласа на многомерном кубе с неядерной резольвентой.
Постановка задачи
Пусть ![]() –
–![]() -мерный куб, где сторона куба
-мерный куб, где сторона куба ![]() .
.
В сепарабельном гильбертовом пространстве ![]() рассмотрим следующие операторы:
рассмотрим следующие операторы:
1) оператор ![]() , порожденный краевой задачей Дирихле:
, порожденный краевой задачей Дирихле:
![]() ,
, ![]() ,
,
где ![]() – оператор Лапласа,
– оператор Лапласа, ![]() – граница куба
– граница куба ![]() ;
;
2) оператор ![]() , порожденный краевой задачей Неймана:
, порожденный краевой задачей Неймана:
![]() ,
, 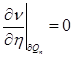 ,
,
где ![]() ,
, ![]() – нормаль к границе
– нормаль к границе ![]() куба
куба ![]() .
.
Введем оператор 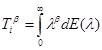 , где
, где ![]() ,
, ![]() – спектральное разложение единицы операторов
– спектральное разложение единицы операторов ![]() ,
, ![]() и
и ![]() при
при ![]() Собственным числам
Собственным числам ![]() оператора
оператора ![]() соответствуют ортонормированные в H собственные функции
соответствуют ортонормированные в H собственные функции ![]() при
при ![]() , и
, и 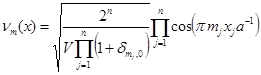 при
при ![]() , где
, где ![]() – мультииндекс
– мультииндекс ![]() ,
, ![]() ,
, ![]()
![]() – символ Кронекера.
– символ Кронекера.
Будем нумеровать упорядоченные по возрастанию собственные числа и собственные функции оператора ![]() через
через ![]() и
и ![]() соответственно, где
соответственно, где ![]() ,
, ![]() ,
, ![]() – кратность собственного числа
– кратность собственного числа ![]() , т.е.
, т.е. ![]() ,
, ![]() .
.
Введем аналитические, ограниченные по модулю (но не в совокупности) в правой полуплоскости ![]() функции
функции ![]()
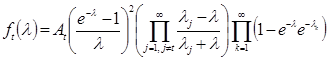 ,
,
где нормирующие множители ![]() выбраны из условия
выбраны из условия ![]() ,
, ![]() . Очевидно, что
. Очевидно, что ![]() , где
, где ![]() – символ Кронекера. Положим
– символ Кронекера. Положим ![]() и пусть
и пусть 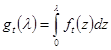 . Очевидно также, что
. Очевидно также, что ![]() ,
, ![]() .
.
Введем следующие обозначения: ![]() – резольвента оператора
– резольвента оператора ![]() ,
, ![]() ,
, ![]()
![]() – вертикальные прямые. Зафиксируем некоторое
– вертикальные прямые. Зафиксируем некоторое ![]() и из последовательности
и из последовательности ![]() выберем максимальную подпоследовательность чисел
выберем максимальную подпоследовательность чисел ![]() , для которых выполняется неравенство
, для которых выполняется неравенство![]() . Объекты, связанные с числом
. Объекты, связанные с числом ![]() , в дальнейшем будем обозначать с использованием верхнего индекса
, в дальнейшем будем обозначать с использованием верхнего индекса ![]() .
.
Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – абсолютная операторная норма (для оператора Гильберта – Шмидта). Заметим, что
– абсолютная операторная норма (для оператора Гильберта – Шмидта). Заметим, что ![]() . Хорошо известна [5] асимптотика собственных чисел оператора
. Хорошо известна [5] асимптотика собственных чисел оператора ![]() , при
, при ![]() :
: ![]() (
(![]() ,
,![]() ), поэтому при
), поэтому при ![]() ряд
ряд ![]() и оператор
и оператор ![]() , где
, где ![]() , суть оператор Гильберта – Шмидта, причем имеет место неравенство:
, суть оператор Гильберта – Шмидта, причем имеет место неравенство: ![]()
![]() ,
,![]()
Рассмотрим комплекснозначную функцию ![]() , где
, где ![]() – пространство измеримых на
– пространство измеримых на ![]() , ограниченных в существенном функций, обладающую следующими свойствами:
, ограниченных в существенном функций, обладающую следующими свойствами:
![]() , (1)
, (1)
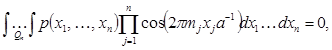
![]()
![]() , (2)
, (2)
![]() (3)
(3)
(![]() ). Функцию
). Функцию ![]() часто называют потенциалом.
часто называют потенциалом.
Обозначим через ![]() – множество функций из пространства
– множество функций из пространства ![]() , обладающих свойствами (1) – (3), а через
, обладающих свойствами (1) – (3), а через ![]() обозначим оператор умножения на рассмотренную выше функцию
обозначим оператор умножения на рассмотренную выше функцию ![]()
Поставим цель – зная собственные числа операторов ![]() ,
, ![]() и некоторые дополнительные условия на функцию
и некоторые дополнительные условия на функцию ![]() , доказать существование и единственность потенциала
, доказать существование и единственность потенциала ![]() во множестве
во множестве ![]() .
.
Результаты исследования
Теорема. Если для комплексной последовательности ![]() существует подпоследовательность
существует подпоследовательность ![]() такая, что выполняются следующие неравенства:
такая, что выполняются следующие неравенства:
(i) 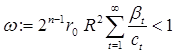 ,
,
(ii) 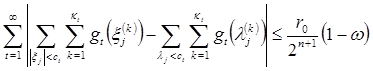 ,
,
то во множестве ![]() существует потенциал
существует потенциал ![]() , такой, что для любого натурального
, такой, что для любого натурального ![]() имеет место равенство:
имеет место равенство:
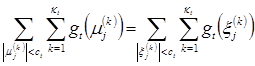 , где
, где ![]() – спектр оператора
– спектр оператора ![]() .
.
Доказательство теоремы, также как и в работах [2, 4, 7], заключается в конструировании сжимающего оператора ![]() :
: ![]() , определяемого равенством:
, определяемого равенством:
![]() , (4)
, (4)
где 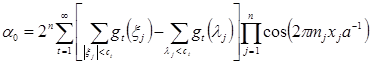 ,
, ![]() , и
, и ![]() ,
, ![]() – регуляризованный след оператора
– регуляризованный след оператора ![]() .
.
Далее доказывается, что оператор (4) является сжимающим на множестве ![]() :
:
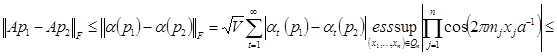
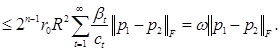
Поскольку выбор подпоследовательности ![]() из последовательности
из последовательности ![]() ограничен лишь неравенством (i), то ее всегда можно выбрать так, чтобы число
ограничен лишь неравенством (i), то ее всегда можно выбрать так, чтобы число 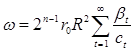 было меньше 1.
было меньше 1.
Итак, согласно принципу сжимающих отображений С. Банаха уравнение ![]() во множестве
во множестве ![]() имеет единственное решение.
имеет единственное решение.
Замечание. Последовательность ![]() , удовлетворяющая условию (ii) существует.
, удовлетворяющая условию (ii) существует.
Заключение
Таким образом, в работе доказана теорема о существовании и единственности симметричного потенциала, восстановленного по кратным спектрам двух краевых задач возмущенной степени многомерного оператора Лапласа с неядерной резольвентой.
Рецензенты:
Кадченко С. И., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики и информатики, ФГБОУ ВПО «МГТУ им. Г. И. Носова», г. Магнитогорск;
Кузнецов В. А., д.ф.-м.н., доцент, заведующий кафедрой высшей математики № 1, ФГБОУ ВПО «МГТУ им. Г. И. Носова», г. Магнитогорск.



