Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы

Белаш А.Н.

Статья описывает обзор существующих обходов планарных графов. Представлена проблема обхода графа по граням (цикл Белаша). Статья описывает главный подход к решению этой проблемы. Материал касается только альфа блока. Некоторые следствия теорем о цикле Белаша представлены в работе. Автор объясняет, где может существовать цикл Белаша.

Статья в формате PDF

140 KB

Введение

Будем говорить, что граф укладывается на поверхности , если его можно так нарисовать на , что никакие два его ребра не пересекаются. Граф называется планарным, если его можно уложить на плоскости; плоский граф – это граф, уже уложенный на плоскости. Области, определяемые плоским графом, назовем его внутренними гранями[1].

На сегодняшний день известны два обхода графа с возвращением в ту вершину, из которой они были начаты:

1)      цикл Эйлера (обход графа по всем ребрам с возвращением в исходную вершину, причем каждое ребро должно быть пройдено только один раз)[1,2];

2)      цикл Гамильтона (обход графа по всем вершинам с возвращением в исходную вершину, причем каждая вершина должна быть пройдена только один раз) [1,2].

Однако ни в одной из известных работ, относящихся к обходам графа с возвращением в исходную вершину, не встречается описание обхода плоской укладки графа по всем внутренним граням с возвращением в исходную вершину.

Основное изложение теорем в этой работе будет относиться к -блоку. Дадим определение -блоку. Пусть мы имеем невзвешенный плоский псевдограф , где  – множество вершин графа ,  – множество ребер графа ,  – множество внутренних граней графа . Назовем внутренними кратными ребрами те кратные ребра, которые не являются смежными с внешней гранью. Назовем внешними те кратные ребра, которые смежны с внешней гранью. Пример внутренних и внешних кратных ребер приведен на рисунке 1.

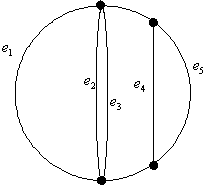
Рис. 1. Пример внутренних и внешних кратных ребер

На рисунке 1 ребра и  являются внешними кратными ребрами, а ребра , , являются внутренними кратными ребрами.

Упростим псевдограф  до графа , который будет представлять собой блок без внутренних кратных ребер следующим образом: если в графе  есть точка сочленения , связывающая два блока и , то для дальнейшего рассмотрения мы возьмем, не теряя общности, блок . Это допустимо, так как дальнейшее изложение аналогично будет и для блока . Допустим, что блок  является мультиграфом (он содержит кратные ребра). Удалим из блока  все внутренние кратные ребра, оставив на местах инцидентных им вершин только одно ребро. После этого преобразования блок  превратится в граф . Но, не теряя общности, мы можем также предположить, что в графе есть множество точек сочленения и соответственно множество блоков. Упрощение псевдографа все равно будет проводиться по схеме предложенной выше. Пример упрощения псевдографа приведен на рисунке 2.

Рис. 2. Пример преобразования графа  в граф 

Назовем тип графов, соответствующих графу  -блоком.

Постановка задачи

Пусть представлен на плоскости  плоский граф , где  – множество вершин графа ,  – множество ребер графа ,  – множество внутренних граней графа . Допустим, что – -блок. Далее обозначим: – вершина графа , , ; – ребро графа , , ; – внутренняя грань графа , , ; – вершина из которой начинается обход графа. Предположим, что при начатом обходе из вершины  мы попадаем в некоторое ребро , которое является смежным с гранями  и  или, не теряя общности, предположим, что  является смежным с гранями ,  (). Тогда пройдя ребро  мы должны принять, что мы прошли строго только одну из граней  или . Отсюда сделаем вывод, что задача успешно решена, если мы построим такую цепь , состоящую из звеньев , , , которая при выходе из вершины  приведет нас также в вершину  пройдя по граням только один раз, ребра также не должны повторятся. Назовем такого вида простую цепь – грань-простой цикл. Таким образом, задача сводится к нахождению общего грань-простого цикла (цикл Белаша) графа . Цепь, которая строится по принципу построения грань-простого цикла, но с конечной вершиной отличной от начальной, назовем грань-простой цепью. Но если такая цепь имеет повторяющиеся грани, то мы ее назовем грань-цепью. А если в цикле повторяются грани, то мы назовем его грань-цикл.

Назовем грань-простой цикл простым самому себе в том случае, если он относится к семейству грань-простых циклов и проходит через различные относящиеся к нему грани только один раз, однако часть этих граней может относиться и к другим циклам из этого семейства. Таким образом, семейство грань-простых циклов будет последовательно покрывать -блок по граням. Ниже мы обоснуем как будет строиться семейство покрывающих-блок циклов.

Пусть  – множество последовательно покрывающих граф грань-простых циклов, , - -ый грань-простой цикл. Возьмем два последовательно следующих друг за другом цикла  и ,. Цикл  будет отличаться от цикла  тем, что он будет проходит только один раз через все грани цикла , но при этом он будет содержать также некоторые грани, смежные с уже пройденными гранями цикла . Если на графе существует цикл Белаша, то им будет грань-простой цикл .

Теорема 1. Пусть граф  – -блок. Если на этом графе найдется такая грань , что относительно нее можно построить семейство грань-простых циклов имеющее общее подмножество вершин  ( ), то последний из этих циклов будет циклом Белаша.

Доказательство. Доказательство проведем методом математической индукции. Шаг индукции обозначим буквой . Построим произвольный граф, удовлетворяющий условиям теоремы и соответствующий шагу индукции  (рис. 3).

Рис. 3. Произвольный -блок для шага индукции 

Построим цикл Белаша для -блока изображенного на рисунке . Этот цикл изобразим на рисунке 4.

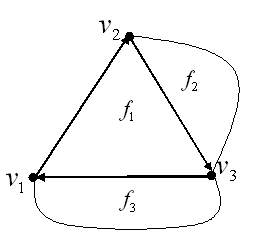
Рис. 4. Цикл Белаша для -блока изображенного на рисунке 3

Из рисунка 4 видна очевидность существования цикла Белаша для произвольного -блока, удовлетворяющего условиям теоремы 1 при . Предположим, что такой цикл существует для произвольного графа  на шаге индукции . Достроим граф  до графа . Продолжим построение семейства грань-простых циклов уже для графа . Предположим, что грань-простые циклы, покрывающие граф , образуют следующее семейство . Если грань-простые циклы покрыли по граням весь граф, то, очевидно, что последний из них цикл  будет циклом Белаша. Но предположим, что только до ,  возможно последовательно покрывать граф  грань-простыми циклами. Иными словами на цикле  остается не пройденная какая-то грань . Эта грань останется не пройденной также и на всех последующих циклах начиная от цикла , так как если бы мы ее могли пройти, то она вошла бы в семейство  до цикла . Очевидно, что в этом случае не будет и существовать цикла Белаша для графа . Отметим также факт, что если на графе вообще не будет существовать грань, относительно которой можно построить семейство , покрывающее весь граф, то на таком графе и не будет цикла Белаша.■

Следствие 1. Пусть  – граф, на котором существует цикл Белаша. Тогда любая вершина , принадлежащая этому циклу, может быть исходной для этого цикла.

СПИСОК ЛИТЕРАТУРЫ:

1.      Харари Ф. Теория графов / Пер. с англ. и предисл. В.П. Козырева. Под ред. Г.П. Гаврилова. Изд.2-е. – М.: Едиториал УРСС, 2003. – 296 с.

2.      Оре О. Теория графов. Главная редакция физико-математической литературы изд-ва «Наука», 1968 – 216 с.

Библиографическая ссылка