Введение
В [1] развита вероятностно-статистическая модель учащегося, в соответствии с которой индивидуум в процессе обучения движется в информационном пространстве. Однако указать точное положение его в этом пространстве не представляется возможным. Это обусловлено тем, что человеческому знанию присущи элементы неопределённости и случайности. В связи с этим можно говорить лишь о вероятности нахождения учащегося в той или иной области информационного пространства. В рассматриваемой модели каждый индивидуум представлен в виде некоторой функции распределения (плотности вероятности) - вероятности найти его в единичном объёме информационного пространства. Данная работа посвящена нахождению экспериментальных функций распределения, эволюция которых характеризует поведение студентов в процессе обучения в высшем учебном заведении.
Экспериментальные функции распределения
В российской системе образования для оценки знаний учащегося используется пятибалльная порядковая шкала. В связи с этим в качестве единицы измерения координаты в информационном пространстве может быть выбран «балл». При этом максимальное продвижение учащегося в информационном пространстве при изучении одной дисциплины составляет 5 баллов. Погрешность в оценке знаний составляет ±0,5 балла. Следовательно, когда студенту выставляется оценка, например, 4 балла, это означает, что его знания находятся в промежутке от 3,5 баллов до 4,5 баллов. Фактически положение индивидуума в информационном пространстве в пересчёте на одну учебную дисциплину в семестр определяется прямоугольной функцией распределения, ширина которой равна 1 баллу в соответствии с погрешностью измерения ±0,5 балла. Эта погрешность настолько большая, что не позволяет наблюдать истинный вид функции распределения. Однако, несмотря на столь грубую аппроксимацию функции распределения, изучение её эволюции позволяет получить важную информацию, как о поведении отдельного индивидуума, так и студенческой группы, и потока в целом.
Таким образом, для простоты рассмотрения задачи экспериментальную функцию распределения индивидуума будем аппроксимировать прямоугольной функцией, ширина которой после первого семестра составляет 1 балл, после второго - 2 балла и т. д. Математическое ожидание (координата центра «тяжести») функции распределения индивидуума после n - го семестра определяется суммой средних оценок, полученных студентом за n семестров, а именно:
![]() ,
,
где ![]() - средняя оценка, полученная студентом в j - ом семестре.
- средняя оценка, полученная студентом в j - ом семестре.
Типичный вид экспериментальной функции распределения индивидуума в различные моменты времени представлен на рис. 1.
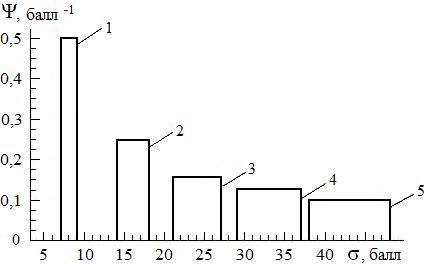
Рис. 1. Типичный вид индивидуальной функции распределения студента на различных этапах обучения: 1 - после первого курса; 2 - после второго курса; 3 - после третьего курса;
4 - после четвёртого курса; 5 - после пятого курса
На рис. 2 изображены зависимости математических ожиданий функций распределения студентов от времени. Видно, что эти зависимости для «сильных» студентов близки к линейным (1). Однако на зависимостях математических ожиданий от времени для «средних» и «слабых» студентов (2 и 3), начиная с 5 семестра, как правило, можно заметить некоторую нелинейность, приводящую к увеличению скорости математических ожиданий (скорости движения студентов в информационном пространстве).
На первый взгляд, может показаться, что это - положительный эффект. Однако, анализ учебных программ, фактического материала по лекциям, семинарам, лабораторным работам и результатов опроса студентов показал, что уровень фундаментализации общетехнических и специальных дисциплин, преподаваемых, начиная с этого времени, сравнительно низкий. В результате сильные студенты "не дорабатывают", а слабым студентам достаточно простого запоминания материала. Кроме того, занижаются требования к сдаче экзаменов.
Такое поведение во времени математических ожиданий индивидуальных функций распределения сказывается и на функциях распределения студенческих групп и потоков (рис. 3). Функции распределения построены в пересчёте на одну учебную дисциплину в семестр для потока студентов (78 человек) одного из технических факультетов Московского государственного института электронной техники. При построении использовался принцип аддитивности, т. е. полная функция распределения находилась как сумма функций распределения всех индивидуумов, отнесённая к их количеству. Анализ показывает, что максимумы функций распределения, соответствующих первым курсам, смещены к их левой границе, а последним курсам - к правой. Это хорошо коррелирует с поведением математических ожиданий функций распределения индивидуумов во времени (рис. 2).
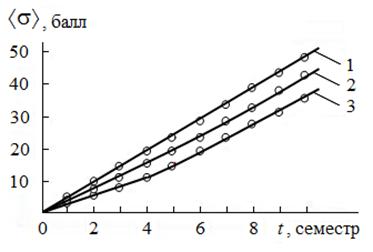
Рис. 2. Зависимость математических ожиданий индивидуальных функций распределения
студентов от времени: 1 - сильный студент; 2 - средний студент; 3 - слабый студент
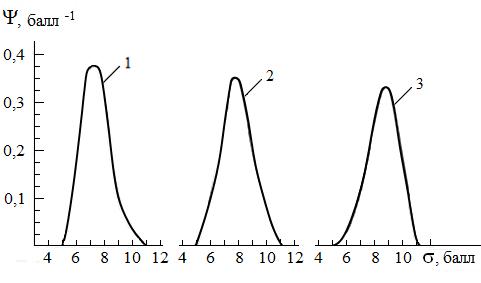
Рис. 3. Функции распределения потока студентов, соответствующие обучению в течение года (аппроксимированы гладкими линиями): 1 - после первого курса; 2 - после третьего курса;
3 - после пятого курса
На рис. 4 представлены экспериментальные данные, характеризующие эволюцию полной функции распределения того же потока студентов с первого по пятый курс. Видно, что по мере продвижения в информационном пространстве функция распределения расплывается. Это происходит вследствие того, что математические ожидания функций распределения индивидуумов движутся с разными скоростями, а сами функции расплываются из-за дисперсии. Следует отметить также, что максимум полной функции распределения в процессе эволюции смещается от её левой границы к центру.
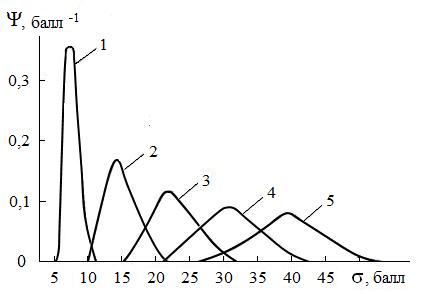
Рис. 4. Эволюция полной функции распределения потока студентов, аппроксимированной гладкими линиями: 1 - после первого курса; 2 - после второго курса; 3 - после третьего курса;
4 - после четвёртого курса; 5 - после пятого курса
Другим важным результатом является перекрывание функций распределения, причём особенно существенное на старших курсах. Это свидетельствует о том, что объём знаний, которыми владеет слабый студент старшего курса (его индивидуальная функция распределения находится в "хвосте" полной функции распределения), может быть значительно меньше объёма знаний, которыми владеет студент младшего курса. Исследования эволюции функций распределения для потоков студентов других факультетов института показало, что функции распределения в информационном пространстве со временем во всех случаях ведут себя идентично. По-видимому, такое поведение функций распределения имеет характер общей закономерности.
Расплывание со временем экспериментальных функций распределения студенческих коллективов свидетельствует о существенной неоднородности студенческой подсистемы. Это приводит к тому, что, начиная с третьего курса, эффективность обучения в таких коллективах резко снижается. В случае больших студенческих групп и потоков преподаватели при проведении занятий, как правило, вынуждены ориентироваться на средних студентов, что при условии наблюдаемой большой дисперсии функции распределения негативно сказывается на учёбе как сильных, так и слабых студентов. Объём и качество сообщаемой информации в этом случае не соответствует потенциальным возможностям сильных и слабых студентов. Сильные студенты работают ниже своих возможностей, а слабые студенты не в состоянии усвоить учебный материал, что приводит к ещё большей неоднородности студенческой подсистемы. Такая ситуация вынуждает преподавателей понижать требования при аттестации студентов.
Взаимодействие студенческой и профессорско-преподавательской подсистем
В общем случае на распространение функции распределения индивидуума в информационном пространстве и во времени оказывают влияние, как свойства студенческой подсистемы, так и профессорско-преподавательской подсистемы. Предположим, что элементарное перемещение математического ожидания функции распределения индивидуума ![]() за время
за время ![]() пропорционально этому интервалу времени и определяется индивидуальными характеристиками студента и свойствами профессорско-преподавательского коллектива ВУЗа, а именно:
пропорционально этому интервалу времени и определяется индивидуальными характеристиками студента и свойствами профессорско-преподавательского коллектива ВУЗа, а именно:
![]() , (1)
, (1)
где ![]() - функция усвоения знаний студентом;
- функция усвоения знаний студентом; ![]() - совокупность параметров, определяющих способность студента усваивать знания (интеллектуальное развитие, психическое и физическое здоровье, потенциальные возможности и др.);
- совокупность параметров, определяющих способность студента усваивать знания (интеллектуальное развитие, психическое и физическое здоровье, потенциальные возможности и др.); ![]() - функционал от функции распределения
- функционал от функции распределения ![]() ;
; ![]() - функция воздействия профессорско-преподавательского коллектива на студенческую подсистему;
- функция воздействия профессорско-преподавательского коллектива на студенческую подсистему; ![]() - совокупность параметров, характеризующих профессиональные и личностные свойства профессорско-преподавательского коллектива.
- совокупность параметров, характеризующих профессиональные и личностные свойства профессорско-преподавательского коллектива.
Из (1) непосредственно следует
![]() , (2)
, (2)
где ![]() - скорость движения математического ожидания в информационном пространстве.
- скорость движения математического ожидания в информационном пространстве.
В соответствии с (2) скорость движения математического ожидания в информационном пространстве определяется произведением функций усвоения знаний ![]() и
и ![]() воздействия , т. е. характеризует взаимодействие студента с профессорско-преподавательской подсистемой. Увеличение скорости движения математических ожиданий индивидуальных функций распределения для средних и слабых студентов, начиная с 5 семестра (рис. 2), а также смещение максимумов полных функций распределения от левой границе к центру на старших курсах (рис. 4), как отмечалось выше, связано с переходом от изучения фундаментальных дисциплин к общетехническим и специальным. Такой переход сопровождается изменением состава профессорско-преподавательского коллектива, ведущего учебно-воспитательную работу на каждом потоке. Тогда, исходя из (2), объяснить наблюдаемое экспериментально поведение
воздействия , т. е. характеризует взаимодействие студента с профессорско-преподавательской подсистемой. Увеличение скорости движения математических ожиданий индивидуальных функций распределения для средних и слабых студентов, начиная с 5 семестра (рис. 2), а также смещение максимумов полных функций распределения от левой границе к центру на старших курсах (рис. 4), как отмечалось выше, связано с переходом от изучения фундаментальных дисциплин к общетехническим и специальным. Такой переход сопровождается изменением состава профессорско-преподавательского коллектива, ведущего учебно-воспитательную работу на каждом потоке. Тогда, исходя из (2), объяснить наблюдаемое экспериментально поведение ![]() можно изменением свойств функции воздействия
можно изменением свойств функции воздействия ![]() .
.
Низкий уровень фундаментализации общетехнических и специальных дисциплин обусловлен негативным изменением совокупности параметров λ, которые должны приводить к уменьшению значений функции воздействия ![]() , и, следовательно, при сохранении прежних высоких требований к уровню знаний - к уменьшению скорости
, и, следовательно, при сохранении прежних высоких требований к уровню знаний - к уменьшению скорости ![]() . Тогда для объяснения наблюдаемого экспериментально увеличения значений
. Тогда для объяснения наблюдаемого экспериментально увеличения значений ![]() на старших курсах необходимо предположить, что в этом случае имеет место существенная методическая погрешность при определении положений математических ожиданий функций распределения индивидуумов в информационном пространстве, обусловленная завышением оценок, получаемых средними и слабыми студентами старших курсов на экзаменах. Анализ фактического материала показал, что на некоторых потоках по ряду специальных дисциплин знания студентов оцениваются фактически по двухбалльной системе ("4" и "5").
на старших курсах необходимо предположить, что в этом случае имеет место существенная методическая погрешность при определении положений математических ожиданий функций распределения индивидуумов в информационном пространстве, обусловленная завышением оценок, получаемых средними и слабыми студентами старших курсов на экзаменах. Анализ фактического материала показал, что на некоторых потоках по ряду специальных дисциплин знания студентов оцениваются фактически по двухбалльной системе ("4" и "5").
Уравнение (2) можно преобразовать к виду
![]() , (3)
, (3)
где ![]() - функция, характеризующая неподатливость (инертность) индивидуума по отношению к изменению его положения в информационном пространстве. Уравнение (3) является фактически аналогом уравнения движения Аристотеля в механике, роль силы в котором выполняет функция воздействия
- функция, характеризующая неподатливость (инертность) индивидуума по отношению к изменению его положения в информационном пространстве. Уравнение (3) является фактически аналогом уравнения движения Аристотеля в механике, роль силы в котором выполняет функция воздействия ![]() , а массы - функция инертности
, а массы - функция инертности ![]() .
.
Для получения информации о свойствах функций воздействия ![]() и инертности
и инертности ![]() необходимо проведение глубоких педагогических, психологических и социологических исследований профессорско-преподавательской и студенческой подсистем. Зная конкретный вид функций воздействия и инертности, можно находить скорости движения математических ожиданий функций распределения индивидуумов в информационном пространстве, и используя затем уравнение движения Аристотеля (3), прогнозировать эволюцию индивидуальных и полной (для студенческой группы, потока) функций распределения. Это позволяет оценивать качество учебно-воспитательного процесса в ВУЗе и вырабатывать рекомендации по его совершенствованию.
необходимо проведение глубоких педагогических, психологических и социологических исследований профессорско-преподавательской и студенческой подсистем. Зная конкретный вид функций воздействия и инертности, можно находить скорости движения математических ожиданий функций распределения индивидуумов в информационном пространстве, и используя затем уравнение движения Аристотеля (3), прогнозировать эволюцию индивидуальных и полной (для студенческой группы, потока) функций распределения. Это позволяет оценивать качество учебно-воспитательного процесса в ВУЗе и вырабатывать рекомендации по его совершенствованию.
Выводы
- 1. Экспериментальные функции распределения, найденные для потока студентов каждого курса, асимметричны относительно их максимальных значений, причём максимум функций распределения для потока студентов младших курсов смещён к их левой границе (в сторону меньших значений координат), а для студентов старших курсов - к правой границе.
- 2. В процессе эволюции функций распределения их дисперсия увеличивается (функции распределения расплываются).
- 3. Скорость движения математического ожидания индивидуальных функций распределения студентов в информационном пространстве пропорциональна функции воздействия профессорско-преподавательского коллектива и обратно пропорциональна функции инертности, характеризующей неподатливость изменению положения математического ожидания в пространстве (аналог закона Аристотеля в механике).
СПИСОК ЛИТЕРАТУРЫ
1. Романов В.П., Соколова Н.А. Вероятностно-статистическая модель учащегося // Современные проблемы науки и образования, № 6 (Часть 3.), 2009.
Библиографическая ссылка
Романов В.П., Соколова Н.А. АНАЛИЗ ПОВЕДЕНИЯ УЧАЩИХСЯ В ПРОЦЕССЕ ОБУЧЕНИЯ В ВЫСШЕМ УЧЕБНОМ ЗАВЕДЕНИИ // Современные проблемы науки и образования. – 2009. – № 6-3. ;URL: https://science-education.ru/ru/article/view?id=1445 (дата обращения: 25.04.2024).



