В последнее время актуальной проблемой в сфере высшего образования является наличие профессионально подготовленных кадров. Вносятся различные изменения в учебные планы, пересматриваются структуры изучаемых дисциплин. Что касается сферы строительного образования, большинство выпускников не имеют начальной базы знаний для работы. Изучаемое в университете и полученные задания на производстве не соединяются в единую систему. На наш взгляд, чтобы теория изучаемых дисциплин и профессиональная практика были неразделимы, необходимо постоянно рассматривать изучаемый материал в приложении к профессиональной сфере деятельности. Это в первую очередь касается не только специальных дисциплин, но и фундаментальных наук, например, математики.
Использование информационных и коммуникационных технологий (ИКТ) помогает усилить профессиональную направленность в решении задач за счет дополнительного рассмотрения справочного математического содержания, углубления знаний о необходимом математическом материале, создания индивидуального темпа просмотра математической составляющей.
Нам хотелось бы рассмотреть пример лекционного занятия по математике на тему «Производная» для будущих строителей с использованием информационных технологий.
В поддержку лекций нами разработан электронный учебник, содержащий теоретический материал определенной структуры (рис. 1).
Рис. 1. Фрагмент электронного учебника
Подготовка преподавателя к лекционным занятиям предусматривает постановку цели лекции, изложение материала лекции (понятий, теорем, методов) и рассмотрение возможности его приложения в профессиональной деятельности. Структура лекции, как правило, имеет следующий вид:
1. Постановка цели лекции и мотивация учебной деятельности. В качестве стимулирующего материала студентам предлагается профессионально ориентированная математическая задача, содержание которой обосновывает необходимость изучения материала лекции для профессиональной деятельности будущего инженера.
2. Изложение основных вопросов лекции, предусматривающее рассмотрение определений понятий, теорем, доказательств теорем, математических методов изучаемой темы. Все это содержание демонстрируется на экране электронного учебника.
3. Первичное усвоение знаний студентами. Оно осуществляется путем их применения к решению как математических, так и профессионально ориентированных задач. В частности, возвращаемся к решению профессионально ориентированной математической задачи представленной в начале лекции.
4. Подведение итогов лекции. При подведении итогов лекции преподаватель выделяет основные положения лекции; отмечает умения, сформировавшиеся у студента; определяет строительную отрасль, в которой математический аппарат данной темы нашел свое применение; выдает задания для самостоятельной проработки. В нашем случае это электронный тест с задачами профессионального характера по изученному материалу.
Рассмотрим на примере темы «Производная» предложенную структуру.
1. Цели данной лекции:
-
ввести и дать определения основным математическим понятиям (производная, геометрический смысл производной, дифференцируемость функции), рассмотреть правила нахождения производных различных функций;
-
проиллюстрировать взаимосвязь изучаемого математического аппарата с такой строительной отраслью как технология и механизация строительного производства;
-
сформировать профессиональные умения: умение применять математический аппарат при вычислении скорости протекания строительных процессов; умение с помощью математических средств исследовать эффективность работы механизмов строительных машин;
-
показать профессионально-практическую значимость темы «Производная» для будущей деятельности инженера-строителя.
Мотивация изучения вопросов связанных с понятием производной достигается при использовании задачи следующего содержания:

Рис.2
После формулировки задачи преподаватель вместе со студентами вырабатывает алгоритм решения подобного типа задач, переходя, таким образом, к определению понятия производной.
К необходимости изучения правил дифференцирования функций студентов можно подвести с помощью такой задачи:
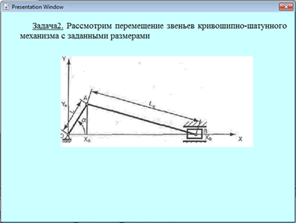
Рис. 3. Фрагмент электронного учебника
Допустим, что начальное положение ведущего звена – кривошипа – равно ![]() =62°. Размеры звеньев кривошипно-шатунного механизма соответственно равны: L=0.1 и Lc=0.35. Уравнение движения кривошипа имеет вид:
=62°. Размеры звеньев кривошипно-шатунного механизма соответственно равны: L=0.1 и Lc=0.35. Уравнение движения кривошипа имеет вид: ![]() .Требуется определить положение, скорость и ускорение ведомого звена – ползуна кривошипнo-шатунного механизма и их значения для заданного угла поворота.
.Требуется определить положение, скорость и ускорение ведомого звена – ползуна кривошипнo-шатунного механизма и их значения для заданного угла поворота.
На данном этапе лекции преподаватель предлагает студентам составить математическую модель задачи. Процесс составления модели можно представить в виде следующего диалога:
- Посмотрите на рисунок, какой отрезок на нем определяет положение ползуна кривошипно-шатунного механизма?
-Отрезок ![]() .
.
- Какую фигуру образуют отрезок ![]() и звенья кривошипно-шатунного механизма L и
и звенья кривошипно-шатунного механизма L и ![]()
- Треугольник ![]()
- Как в треугольнике ![]() можно представить отрезок
можно представить отрезок ![]() ?
?
- Как сумму векторов ![]() и
и ![]() , т. е.
, т. е. ![]() .
.
- Т. о. получили уравнение связей механизма в векторной форме. Можно ли представить это уравнение в другой форме?
- Да. Так как нам известен угол ![]() , то мы можем найти проекции векторов на оси и записать уравнение связи в координатной форме.
, то мы можем найти проекции векторов на оси и записать уравнение связи в координатной форме.
![]()
![]()
![]() или
или
![]()
Уравнение ![]() является математической моделью задачи. Так как
является математической моделью задачи. Так как ![]() определяет положение (перемещение) ползуна, то нахождение линейной скорости ползуна и линейного ускорения ползуна сводится к нахождению первой и второй производной уравнения связи. Это приводит нас к необходимости изучения правил нахождения производной и изложению основных вопросов по данной теме.
определяет положение (перемещение) ползуна, то нахождение линейной скорости ползуна и линейного ускорения ползуна сводится к нахождению первой и второй производной уравнения связи. Это приводит нас к необходимости изучения правил нахождения производной и изложению основных вопросов по данной теме.
2. Изложение основных вопросов лекции предполагает рассмотрение понятий производная функции, геометрический смысл производной, дифференцирование функций, правил дифференцирования функций. Все наглядно представлено перед студентами на страницах электронного учебника.
3. Первичное усвоение знаний по использованию правил дифференцирования функций осуществляется в процессе исследования построенной в начале лекции математической модели задачи 2. В исследовании этой модели выделяют следующие этапы:
а) аналитическое вычисление скорости ползуна путем дифференцирования уравнения положения ползуна и нахождение значения скорости для заданного угла поворота:
![]() ;
;
б) определение значения скорости ползуна для заданного угла поворота;
в) аналитическое вычисление ускорения ползуна путем дифференцирования уравнения скорости ползуна и нахождение значения ускорения для заданного угла поворота:
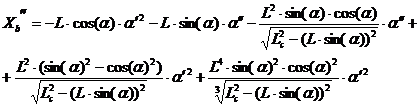 ;
;
г) определение значения ускорения ползуна для заданного угла поворота;
д) определение положения ползуна для заданного угла поворота.
4. При подведении итогов лекции преподаватель выделяет ключевые положения лекции и подчеркивает важность аппарата данной темы для такой строительной отрасли как технология и механизация строительного производства. Отмечается, что решение подобных типов задач вырабатывает у будущего инженера-строителя умение применять математический аппарат при вычислении скорости протекания строительных процессов и умение с помощью математических средств исследовать эффективность работы механизмов строительных машин. Сказанное убеждает студентов в необходимости изучения данной темы и вырабатывает у них потребность использовать изученный математический материал в решении профессиональных задач. В конце изученной темы нами разработан тест, служащий для проверки уровня усвоения знаний и содержащий задачи прикладного характера.
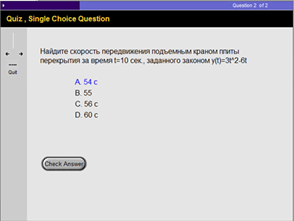
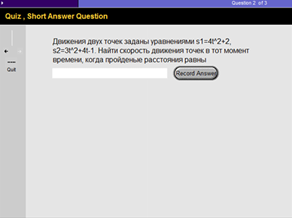
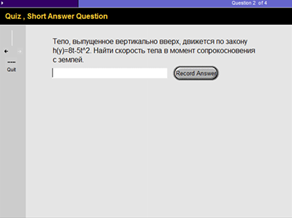
Рис.4
Таким образом, дополнительное использование электронного учебника позволит реализовать более углубленное, расширенное, детальное изучение полученных на лекции знаний и сформированных умений.
Рецензенты:
Усманов В.В., д.п.н., профессор, первый проректор, проректор по научной работе, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Родионов М.А., д.п.н., профессор, зав.кафедрой «Алгебры и методики преподавания математики и информатики», ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.
Библиографическая ссылка
Акимова И.В., Титова Е.И., Чапрасова А.В. ПРИМЕНЕНИЕ ИКТ НА ЗАНЯТИЯХ ПО МАТЕМАТИКЕ У СТУДЕНТОВ СТРОИТЕЛЬНЫХ СПЕЦИАЛЬНОСТЕЙ ДЛЯ РАЗВИТИЯ ПРОФЕССИОНАЛЬНОЙ НАПРАВЛЕННОСТИ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=15260 (дата обращения: 25.04.2024).



