Как известно, ортонормированная система Хаара была применена во многих исследованиях по теории вложения классов функций [2-3], к примеру, вложения классов ![]() , где
, где ![]() - заданный модуль гладкости общего вида, исследования по которому начались из работ П.Л. Ульянова [8], а затем имели определенные развития (см., напр., в [1], [2-3], [5-7]).
- заданный модуль гладкости общего вида, исследования по которому начались из работ П.Л. Ульянова [8], а затем имели определенные развития (см., напр., в [1], [2-3], [5-7]).
Данные исследования тесно связаны с цифровой обработкой сигнала, а именно, с преобразованием непрерывного сигнала в дискретный, т.е. рекуррентным соотношением в некотором ортогональном базисе [4], а именно, данную ортонормированную систему функций следует преобразовать сохраняя ортогональность, затем можно принять в качестве импульса сигнала, исследуя влияние введенного параметра при разложении непрерывного сигнала в виде суммы дискретных функций.
В данной работе, система Хаара, в определенном смысле, обобщается, а именно, вводится некоторый параметр ![]() , доказывается ортонормированность введенной системы и и исследуется влияние данного параметра в разложении некоторой (степенной) функции в ряд по определенной системе, причем устанавливается условие на введенный параметр. Дальнейшим продолжением теоретических исследований, предполагается исследования по разложению сигналов не степенного вида, а функции из класса
, доказывается ортонормированность введенной системы и и исследуется влияние данного параметра в разложении некоторой (степенной) функции в ряд по определенной системе, причем устанавливается условие на введенный параметр. Дальнейшим продолжением теоретических исследований, предполагается исследования по разложению сигналов не степенного вида, а функции из класса ![]() .
.
Работа состоит из двух разделов. В первом разделе определяется система типа Хаара и доказывается ортонормированность. Во втором разделе определяются коэффициенты разложения степенной функции по ортогональной системе функций.
1 Ортонормированная система типа Хаара
Определение. Пусть даны числа ![]() и целое
и целое ![]() . Систему функций
. Систему функций ![]()
![]() , определенную в виде
, определенную в виде
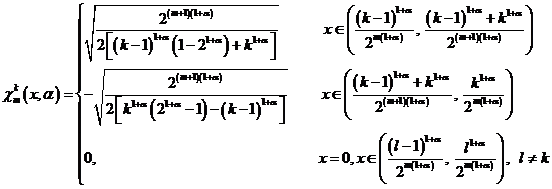
назовем системой типа Хаара.
Замечание. Данная система определена по аналогии определения системы Хаара.
Справедлива
Теорема 1. Пусть даны число ![]() и целое
и целое ![]() . Тогда определенная на сегменте
. Тогда определенная на сегменте ![]() система типа
система типа ![]()
![]() вида (
вида (![]() ,
, ![]() и
и 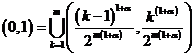 )
)
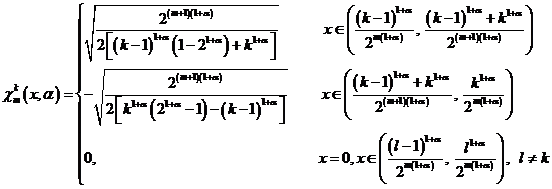 (1)
(1)
является ортонормированной системой функций.
Доказательство. Покажем нормированность системы, т.е. справедливость
![]() . (2)
. (2)
Пусть ![]() и
и ![]() . Тогда
. Тогда
![]() . (3)
. (3)
Действительно, при ![]() и
и ![]() , имеем
, имеем
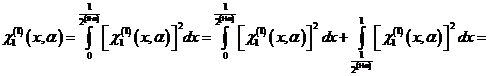
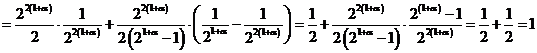 .
.
Теперь, при ![]() и
и ![]() , получим
, получим
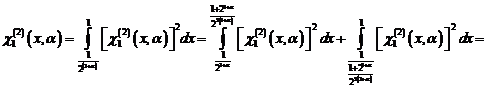
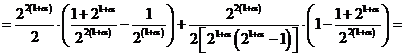
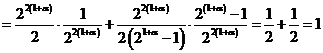 ,
,
тем самым, (3) доказано. Дя любого ![]() докажем соотношение (2). В самом деле, для
докажем соотношение (2). В самом деле, для
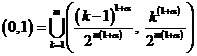 ,
,
будем иметь
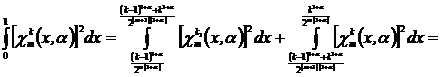
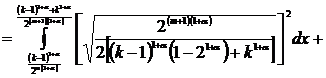
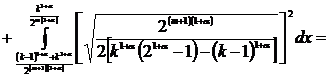
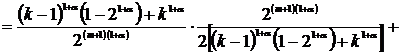
![]() ,
,
т.е. соотношение (2) доказано.
Теперь покажем ортогональность системы при ![]()
![]() . Для этого достаточно показать справедливость
. Для этого достаточно показать справедливость
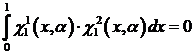 . (4)
. (4)
Действительно, по определению функций, произведение функций равно нулю, а именно, справедливо

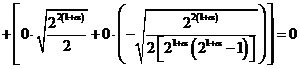 ,
,
поэтому,
 .
.
Отсюда, теорема для случая ![]()
![]() доказана. Рассмотрим следующий случай.
доказана. Рассмотрим следующий случай.
Пусть ![]() ,
, ![]() и
и ![]() . Сначала, предположим
. Сначала, предположим ![]() . Тогда, если
. Тогда, если
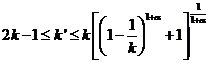 ,
,
то
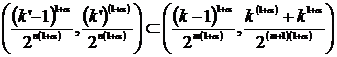 . (5)
. (5)
Отсюда
![]()
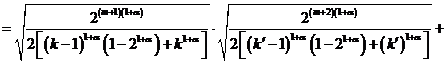
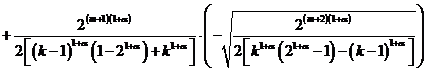 .
.
Из последнего равенства
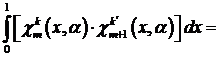
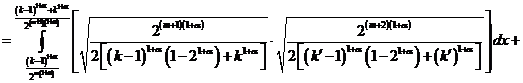
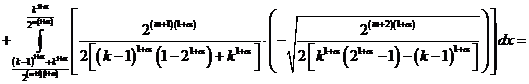
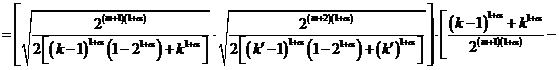
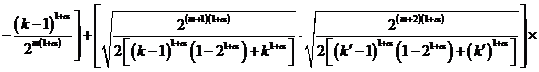
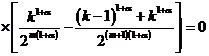 .
.
Для случая
 ,
,
справедливо
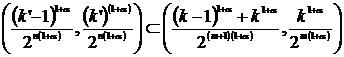 . (6)
. (6)
Тогда
![]()
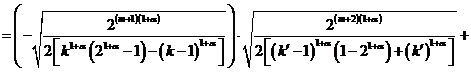
 .
.
Из данного равенства получим
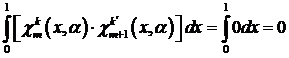 .
.
Если ![]() .
. ![]() и
и ![]() , то
, то
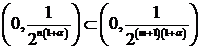 ,
,
а при ![]()
![]() .
.
Поэтому, для случаев ![]() ,
, ![]() и
и ![]() , а вместе с ними и для
, а вместе с ними и для ![]()
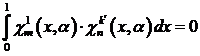 .
.
Пусть ![]() ,
, ![]() . В этом случае, можно повторить рассуждения, приведенные выше.
. В этом случае, можно повторить рассуждения, приведенные выше.
Теорема 1 доказана полностью.
2 Разложение функции ![]() по ортонормированной системе функций
по ортонормированной системе функций
Рассмотрим некоторое простое приложение введенной ортонормированной системы функций для практического разложения функции. Имеет место
Теорема 2. Пусть даны числа ![]() ,
, ![]() и целое
и целое ![]() . Для функции
. Для функции ![]() на промежутке
на промежутке ![]() имеет место следующее
имеет место следующее
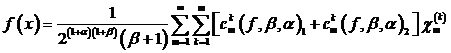 , (7)
, (7)
где,
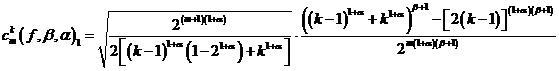 ,
,
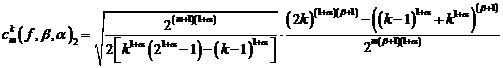 .
.
Доказательство. Сначала рассмотрим случай ![]() ,
, ![]() . Определим коэффициенты разложения следующим образом
. Определим коэффициенты разложения следующим образом
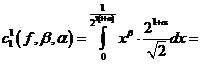
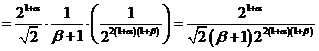
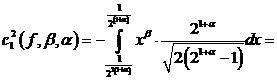
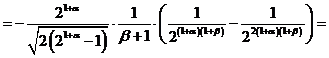
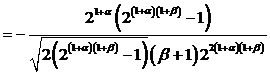 .
.
Таким образом, при ![]() ,
, ![]()
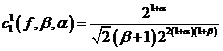
и
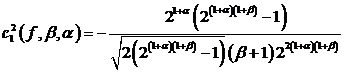 .
.
При ![]() ,
, ![]() , имеем
, имеем
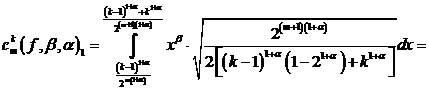
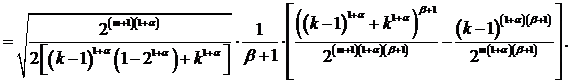

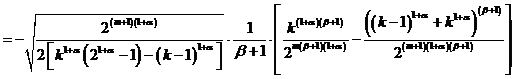 .
.
Отсюда, при ![]() ,
, ![]()
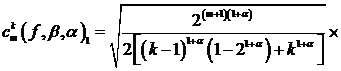
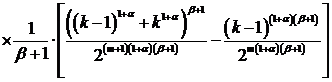
и

 .
.
Таким образом, коэффициенты разложения будут иметь вид
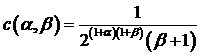
и
![]()
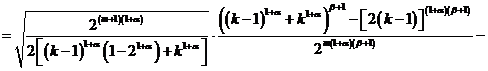
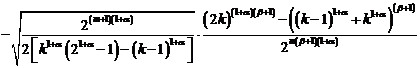 .
.
Теорема 2 доказана полностью.
Рецензенты:
Адамов А.А., д.т.н., профессор, заведующий кафедрой «Математического и компьютерного моделирования» ЕНУ им. Л.Н. Гумилева, г.Астана;
Тусупов Ж.А., д.ф.-м.н., профессор, заведующий кафедрой «Информационные системы» ЕНУ им. Л.Н. Гумилева, г.Астана.
Лубенцов В.Ф., д.т.н., профессор, зам.директора по научной работе, профессор кафедры «Информационные системы, Электропривод и автоматика», Невинномысский технологический институт ГОУ ВПО «Северо-Кавказский государственный технический университет», г.Невинномысск.
Библиографическая ссылка
Султанкулова А.Л., Тохаева А.О., Серикбаева Г.И., Сулейменова Н.К., Сулейменов К.М. ОБ ОДНОМ МЕТОДЕ РАЗЛОЖЕНИЯ ФУНКЦИЙ ПО ОРТОНОРМИРОВАННОЙ СИСТЕМЕ ФУНКЦИЙ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=15294 (дата обращения: 26.04.2024).



