Основным направлением совершенствования современного российского высшего образования в условиях его модернизации является повышение качества обучения [4, 8] и контроля знаний в рамках системного мониторинга качества этапов образовательного процесса и его результатов [3, 7, 9]. Создание информационных баз данных о состоянии всех элементов системы образования, многообразие и разнородность показателей эффективности образовательной деятельности вузов предполагает использование методов многомерного статистического анализа, позволяет проводить различные виды статистического анализа (корреляционный, дисперсионный, факторный, кластерный) и делать выводы об эффективности функционирования всей образовательной системы и составляющих ее подсистем [1, 2, 5].
В данной работе проведен многомерный статистический анализ результатов оценивания знаний по высшей математике в 1-ом семестре по унифицированной дисциплине «Математика 1.1», в состав которой входили модули: линейная алгебра и аналитическая геометрия и дифференциальное исчисление, студентов очной формы обучения Физико-технического института Томского политехнического университета (выборка ФТИ объема n =175) . Для этого были использованы следующие 4 показателя:
- ВК – результаты входного контроля знаний по математике в рамках школьной программы, проводившегося в тестовой форме,
- АТТ1 – результаты текущей аттестации по дисциплине в середине семестра,
- АТТ2 – результаты текущей аттестации по дисциплине в конце семестра,
- ЭКЗ – результат экзамена, проводимого в традиционной форме.
Результаты представлены на (рис.1). Для удобства восприятия все числовые результаты приведены к единой 5-балльной шкале (набранные студентами итоговые баллы делились на максимальный балл, который можно было получить за семестр, и результат деления умножался на пять). Таким образом, в MS Excel была создана база данных, которая обрабатывалась в пакете Statistica [6] для статистического анализа данных.
Согласно корреляционному анализу выявлены высоко значимые (с уровнем значимости р < 0,0005) положительные корреляционные зависимости между АТТ1, АТТ2 и ЭКЗ (коэффициенты парных корреляции Пирсона r и Спирмена R > 0,79).
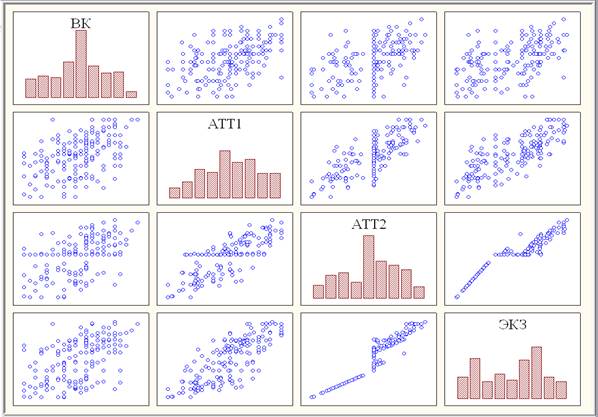
Рис. 1. Диаграммы рассеяния с гистограммами переменных выборки ФТИ
Поэтому в дальнейшем методом главных компонент количество исходных показателей было сокращено до двух, в первую группу Ф1 объединились АТТ1, АТТ2 и ЭКЗ, а во вторую – Ф2 показатель ВК. На основании факторного анализа была проведена интерпретация новых факторных переменных Ф1 и Ф2 по нагрузкам, характеризующим корреляции между факторами и показателями (табл. 1).
Таблица 1
Вращаемые факторные нагрузки в выбранной 2-х факторной модели ФТИ
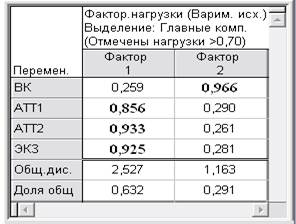
Анализ таблицы 1 показывает, что высокие факторные нагрузки исходных показателей для обоих факторов Ф1{АТТ1+АТТ2+ЭКЗ} и Ф2 {ВК} характеризуются положительной корреляционной связью.
Дальнейший анализ результатов успеваемости 10 групп студентов ФТИ в рамках построенной 2-х факторной модели проводился в системе координат {Ф1, Ф2}. Для определения количества кластеров использовался метод древовидной кластеризации. На рис. 2 показано иерархическое дерево, по которому 10 групп оказались разбиты на 4 кластера, и это разбиение устойчиво относительно вариации мер близости и правил объединения двух кластеров.
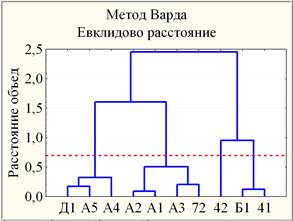
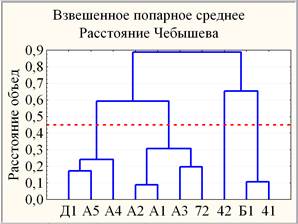
Рис. 2. Дендрограммы наблюдений в пространстве {Ф1, Ф2}, построенные с использованием разных мер близости и правил объединения двух кластеров
Далее в 2-х мерном факторном пространстве {Ф1, Ф2} методом K-средних, проведена классификация учебных групп. В результате была получена также 4-х кластерная высококачественная модель результатов ФТИ, распределяющая 10 учебных групп студентов по 4-м кластерам высоко значимо (на уровне значимости р < 0,0005) согласно λ-критерию Уилкса по совокупности показателей Ф1 и Ф2 (рис. 3).
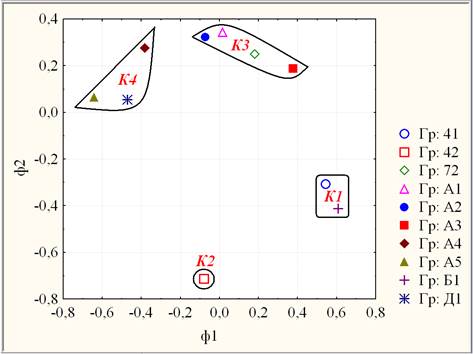
Рис. 3. Диаграмма рассеяния кластеров ФТИ в факторных координат {Ф1, Ф2}
Для оценки качества кластеризации по каждому фактору применялся параметрический дисперсионный анализ (табл. 2).
Таблица 2
Результаты дисперсионного анализа кластеризации наблюдений по факторам ФТИ
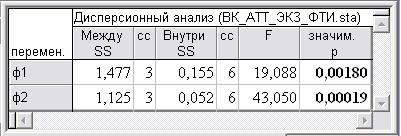
Из табл. 2 следует, что по фактору Ф2 три кластера различаются высоко значимо
(р » 0,0002 < 0,0005), а по фактору Ф1 различаются сильно значимо (0,0005 < р »0,002< 0,005).
Кластерные средние m по четырем исходным {ВК, АТТ1, АТТ2, ЭКЗ} и двум новым {Ф1, Ф2} показателям приведены в табл. 3.
Таблица 3
Кластерные средние m по ВК, АТТ1, АТТ2, ЭКЗ, Ф1, Ф2
|
Кластер |
АТТ1 |
АТТ2 |
ЭКЗ |
Ф1 |
Ф2 |
ВК |
Состав |
|
К1 |
3,108 |
3,241 |
2,934 |
0,576 |
-0,359 |
2,196 |
41+Б1 |
|
К3 |
3,236 |
2,711 |
2,471 |
0,111 |
0,282 |
2,746 |
А1+А2+А3+72 |
|
К4 |
2,005 |
2,276 |
1,855 |
-0,504 |
0,140 |
2,431 |
А4+А5+Д1 |
|
К2 |
2,241 |
2,380 |
2,089 |
-0,078 |
-0,714 |
1,611 |
42 |
Используя апостериорные критерии Фишера, Шеффе, Тьюки, результаты множественных сравнений кластерных средних можно представить в порядке их убывания в пределах каждого фактора:
Ф1: {К1}, {К3, К2}, {К4}. При этом К1 отличается от К3, а К2 – от К4 – слабо значимо ( 0,10 < р < 0,05); К1 отличается от К4 сильно значимо (0,0005 < р < 0,005).
Ф2: {К3, К4}, {К1, К2}. При этом К4 отличается от К1 статистически значимо (0,005< р < 0,05).
Можно отметить, что построенные последовательности неоднородных групп кластеров по каждому фактору подтверждаются результатами множественных сравнений по непараметрическому критерию Краскела-Уоллиса. Для фактора Ф1 отличие К1 от К4 становится статистически значимым ( 0,005< р < 0,05), а для Ф2 отличие К1 от К3 становится слабо значимым (на уровне значимости 0,05< р < 0,10).
Графики кластерных средних для каждого фактора приведены на рис. 4.
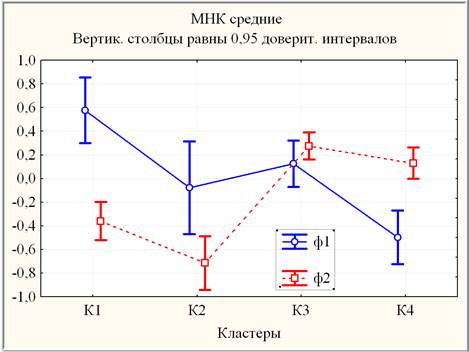
Рис. 4. Линейные графики факторных (стандартизированных) средних с 95% границами доверительных интервалов для каждого кластера
Полученные результаты кластерного анализа наблюдений по совокупности факторов с учетом результатов множественных сравнений кластерных средних для каждого фактора позволяют провести классификацию наблюдений в порядковой шкале стандартизированных измерений (табл. 4), при этом за «Средний» был принят интервал (-0,3; +0,3), интервал «Выше среднего» составлял (+0,3; +1) и, наконец, интервал (-1; -0,3) считался «Ниже среднего».
Таблица 4
Классификация наблюдений по совокупности факторов в порядковой шкале стандартизированных измерений.
|
Кластер |
Объем кластера |
ф1 {АТТ+ЭКЗ} |
ф2 {ВК} |
|
К1 |
2 |
Выше среднего |
Ниже среднего |
|
К2 |
1 |
Средний |
Ниже среднего |
|
К3 |
4 |
Средний |
Средний |
|
К4 |
3 |
Ниже среднего |
Средний |
Согласно рис. 3-4 и табл. 3-4, четыре группы студентов (К3) демонстрируют стабильный «Средний» уровень (mВК » 2,75 и mАТТ2 » 2,71), три группы – статистически значимую положительную динамику (две группы К1 от mВК » 2,20 до mАТТ2 » 3,24, а также еще одна К2 от mВК » 1,61 до mАТТ2 » 2,38) и три группы (К4) – статистически значимую отрицательную динамику (от mВК » 2,43 до mАТТ2 » 2,28).
Выводы
1. Анализа показал положительную корреляционную зависимость между АТТ1, АТТ2 и ЭКЗ (коэффициенты парных корреляции Пирсона r и Спирмена R > 0,79) при высоком уровне значимости р < 0,0005. С учетом корреляционной зависимости показателей методом главных компонент построены Ф1 – фактор текущей успеваемости {АТТ1+АТТ2+ЭКЗ} и Ф2 – фактор ВК.
2. В пространстве {Ф1, Ф2} методом K-средних получена 4-х кластерная значимая модель, распределяющая 10 групп студентов по 4-м кластерам.
3. Для каждого фактора выделены однородные группы кластеров.
4. Классификация результатов оценивания усвоенных студентом знаний по дисциплине «Математика 1.1» осуществлялась в номинальной шкале измерений.
5. Предложенный метод оценки результатов успеваемости студентов может быть использован в учебном процессе для оценки качества обучения и контроля знаний.
Работа выполнена при поддержке Российского научного фонда.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск;
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Терехина Л.И. ПРИМЕНЕНИЕ ФАКТОРНОГО ПОДХОДА КЛАСТЕРИЗАЦИИ РЕЗУЛЬТАТОВ МОНИТОРИНГОВОЙ ОЦЕНКИ ЗНАНИЙ ПО МАТЕМАТИКЕ В ВУЗЕ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18605 (дата обращения: 19.04.2024).



