Для оценки обоснованности проводимых организационных и инженерно-технических мероприятий по повышению уровня стратегии управления денежными потоками предприятия необходимо проведение анализа и определения на его основе экономической эффективности инвестиций, необходимых для реализации предлагаемых мероприятий.
Инвестиции – вложения капитала с целью получения прибыли [3].
Приведем пример использования математических моделей инвестиционного анализа для расчета основных показателей эффективности, связанных с повышением уровня стратегии управления денежными потоками предприятия. Инвестиционный анализ – это комплекс методических и практических приемов и методов разработки, обоснования и оценки целесообразности осуществления инвестиций с целью принятия инвестором эффективного решения.
Алгоритм оценки эффективности инвестиций предполагает выполнение:
1) формализации содержания управленческого решения;
2) определения уровня норматива эффективности инвестиций;
3) оценки величины инвестиций;
4) оценки финансовых результатов инвестиций;
5) расчета основных показателей оценки эффективности инвестиционного решения.
Пусть для реализации инвестиционного проекта предприятию понадобятся капитальные вложения в размере 906000 рублей.
В таблице 1 представлен прогноз величины денежного потока по годам реализации проектных решений.
Таблица 1
Оценка экономической эффективности проектных решений, тыс. р.
|
Показатели |
Размер инвестиции |
Доходы от инвестиций в году № |
|||
|
1 |
2 |
3 |
4 |
||
|
Финансовый результат |
906 |
225 |
375 |
425 |
410 |
Цели и методы
Исходя из приведенных данных, сравним финансовые показатели эффективности указанных мероприятий, рассчитанные с использованием разных математических моделей.
Для сравнения выделим следующие параметры денежных потоков, генерируемых инвестиционным проектом: сумму (NV, NPV, MNPV), доходность (NRR, IRR, MIRR, MIRR(бар)), индекс доходности (DPI) и срок окупаемости (окупаемость, ТС-окупаемость, дюрация). В инвестиционном анализе выделяют три типа математических моделей, определяющих эти параметры [1, 5].
Математическая модель 1. В модель входят только денежные потоки (приток и отток денежных средств – CF и С0 соответственно). Определяются параметры текущая стоимость NV и срок окупаемости инвестиций PP.
Математическая модель 2. Кроме денежных потоков CF, С0 модель использует ставку дисконта r. Определяются параметры: внутренняя норма доходности IRR, чистая текущая стоимость NPV, дисконтированный индекс доходности DPI, чистая норма доходности NRR, дюрация D, дисконтированный срок окупаемости DPP, окупаемость в терминах текущей стоимости TС-окупаемость и модифицированная внутренняя норма доходности с реинвестицией по цене капитала MIRR(бар). В этой модели добавляется учет изменения стоимости денег во времени (с помощью r).
Математическая модель 3. В модели кроме денежных потоков и ставки дисконта используется уровень реинвестиций d. Определяются параметры: модифицированная внутренняя норма доходности MIRR, модифицированная чистая текущая стоимость MNPV и модифицированная чистая норма доходности MNRR. Добавляется, кроме учета изменения стоимости денег во времени, учет нормы доходности реинвестиций (с помощью d).
Результаты
Используя данные из табл. 2, определим параметры из группы «сумма» денежных потоков, генерируемых инвестиционным проектом, для разных математических моделей.
Текущая стоимость NV (математическая модель 1) – это арифметическая сумма всех спрогнозированных денежных потоков (оттоков и притоков), порожденных инвестицией или накопленный эффект (сальдо денежного потока) за расчетный период [4]. Применяется для расчета коэффициентов ликвидности и платежеспособности, иногда для грубой оценки. Расчет производится по следующей формуле:
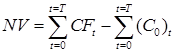 , (1)
, (1)
где NV – текущая стоимость (Net Value);
Т – срок реализации проекта, лет;
СFt – приток денежных средств t-го года (Cash Flow);
(Со)t – отток денежных средств t-го года (абсолютное значение).
Критерий приемлемости: NV >= 0 (чем больше, тем лучше).
В нашем случае текущая стоимость после внедрения мероприятий составит:
NV= 225 + 375 + 425 + 410 – 906 = 529 тыс.р. (2)
То есть, опираясь на показатель NV, проект может быть одобрен.
При тех же исходных показателях (табл. 2), вычислим чистую текущую стоимость по проекту, которая определяется дисконтированием разницы между годовыми оттоками и притоками денег по проекту, накапливаемыми в течение жизни проекта:
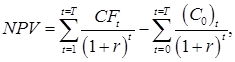 (3)
(3)
где NPV – чистая текущая стоимость (Net present value);
r – ставка дисконта.
В нашем случае чистая текущая стоимость после внедрения мероприятий при ставке дисконта, например 14%, составит:
 (4)
(4)
Расчет NPV – стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведенную к настоящему моменту времени с учётом разной временно́й стоимости денег. Если NPV больше 0, то инвестиция экономически эффективна, а если NPV меньше 0, то инвестиция экономически невыгодна (то есть альтернативный проект, доходность которого принята в качестве ставки дисконтирования требует меньших инвестиций для получения аналогичного потока доходов). Сравнивая (2) и (4), видим, что хотя инвестиционный проект еще остается эффективным, расчет NPV дает более низкую прогнозную оценку изменения экономического потенциала предприятия в случае принятия рассматриваемого проекта.
При расчете NPV, как правило, используется постоянная ставка дисконтирования, однако в зависимости от обстоятельств (например, ожидается изменение уровня процентных ставок) ставка дисконтирования может дифференцироваться по годам. Если в ходе расчетов применяются различные ставки дисконтирования, то пользуются методикой расчетов из [2]. При этом проект, приемлемый при постоянной ставке дисконтирования, может стать неприемлемым.
В случае, когда ставка дисконта и уровень реинвестиций существенно различаются, имеет смысл (с точки зрения точности) рассчитывать NPV по следующей формуле математической модели 3 (учитывающей, что полученные в результате инвестиции средства, реинвестируются по другой ставке):
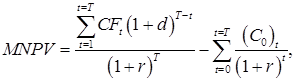 (5)
(5) ![]()
где MNPV – модифицированная чистая текущая стоимость (Modified net present value);
d – уровень реинвестиций, доли единицы.
Определяется: как cумма текущих стоимостей всех спрогнозированных, с учетом ставки дисконта и уровня реинвестиций, денежных потоков.
Критерий приемлемости: MNPV >= 0 (чем больше, тем лучше).
В нашем случае модифицированная чистая текущая стоимость после внедрения мероприятий при той же ставке дисконта 14% и уровне реинвестиций, например 4,5% , составит:
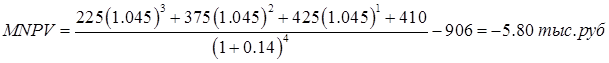 (6)
(6)
Видно, что наиболее точные расчеты эффективности инвестиции (по математической модели 3) показывают непригодность рассматриваемого инвестиционного проекта при заданных параметрах.
Другими параметрами для оценки рисков инвестиционных проектов являются параметры группы «доходность»: NRR, IRR, MIRR, MIRR(бар) и DPI. Сравним некоторые из них для выбранного проекта.
Если данных о ставке дисконта и уровне реинвестиций нет, то используют параметр IRR – внутренняя норма доходности (internal rate of return).
Внутренняя норма доходности – это норма дисконта, при которой уравновешивается текущая стоимость притоков денежных средств и текущая стоимость их оттоков, образовавшихся в результате реализации инвестиционного проекта. Если внутренняя норма доходности по проекту больше требуемой инвестором отдачи, то проект принимают, ниже – отклоняют. То есть IRR = r, при котором NPV = f(IRR) = 0. Таким образом, IRR находят из решения уравнения:
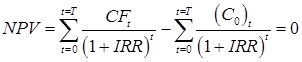 (7)
(7)
Задача может быть решена, например методом последовательного приближения или графическим методом (рис. 1).
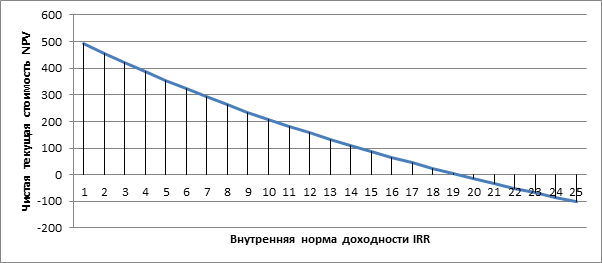
Рис. 1. График зависимости NPV(IRR)
В результате решения уравнения (7) получаем внутреннюю норму доходности, равную: IRR = 19,23 % (IRR > г). Следовательно, с точки зрения данного показателя, проект может быть принят.
Одним из вариантов модификации понятия окупаемости заключается в в нахождении отношения суммы всех дисконтированных денежных потоков (доходов от инвестиций) к дисконтированному инвестиционному расходу. Результатом и является дисконтированный индекс рентабельности DPI (Discounted Profitability Index) (8), где r по-проежнему барьерная или дисконтная ставка:
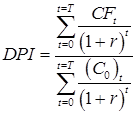 . (8)
. (8)
Критерий приемлемости: DPI >= 1,0 (чем больше, тем лучше).
Используя данные примера при знасении r=14% получим дисконтированный индекс рентабельности равным 1,5.
Наконец, наиболее точно определить рентабельность инвестиции в относительных значениях позволяет параметр из математической модели 3, называемый модифицированной внутренней нормой доходности (Modified internal rate of return) MIRR - скорректированная с учетом нормы реинвестиции внутренняя норма доходности. Формула для расчета модифицированной внутренней нормы доходности (MIRR):
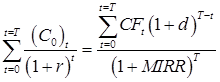 , (9)
, (9)
где d – по-прежнему норма реинвестиций в долях единицы.
Используя параметры рассматриваемого проекта при r =14% и выбрав d=6.5% (при этом модифицированная чистая текущая стоимость составит 17,5 тыс. руб.), получим:
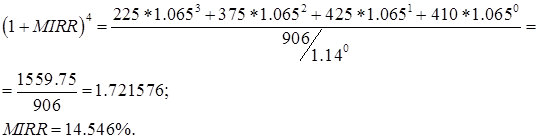 (10)
(10)
Таким образом, модифицированная внутренняя норма рентабельности равна 14,546%, что больше нормы реинвестиций (6,5%), это означает, что проект можно реализовывать.
Выводы
Математическая модель 1 оценки эффективности проектных решений простые методы оценки, относящиеся к числу наиболее старых и которые широко использовались еще до того, как концепция дисконтирования денежных потоков приобрела всеобщее признание в качестве способа получения самой точной оценки приемлемости инвестиций. Однако эти методы и в настоящее время используются разработчиками и аналитиками инвестиционных проектов. С помощью такого рода методов возможно получение некоторой дополнительной информации, что позволяет снижать риск неудачного вложения денежных средств.
Математическая модель 2 содержит динамические методы оценки. Они учитывают дисконтирование как метод оценки инвестиционных проектов путем выражения будущих денежных потоков связано с реализацией проектов через их стоимость на текущий момент времени. Дисконтирование денежных потоков представляет собой приведение разновременных значений к их ценности на определенный момент времени. Данный момент времени называется моментом приведения, который может не совпадать с базовым периодом. Дисконтирование применяется к денежным потокам, выраженным в текущих или дефлированных ценах. Основным экономическим нормативом, используемым при дисконтировании, является норма дисконта, которая выражается в долях единицы или в процентах в год. Норма дисконта является задаваемым экономическим нормативом, используемым при оценке эффективности инвестиционного проекта. Однако в отдельных случаях значение нормы дисконта можно устанавливать различным для разных шагов расчета.
Надо заметить, что одна из проблем, которые возникают при применении дисконтированных оценок для экономической характеристики инвестиционных проектов, состоит в разнонаправленности выводов о целесообразности реализации этих проектов при использовании различных методов расчета. Тем не менее, указанные методы за счет более точных характеристик дают четкое представление о приемлемости принятия важных управленческих решений для реализации будущего инвестиционного проекта.
Математическая модель 3 также является динамической и, наряду с учетом дисконтирования денежных средств, учитывает использование реинвестиций при реализации мероприятий инвестиционного проекта.
Понятно, что ни одна из рассмотренных математических моделей не учитывает условия неопределенности. Хотя можно утверждать, что если с высокой вероятностью известен достоверный прогноз ставки дисконта и уровень реинвестиций, то наиболее точно характеризуют эффективность (рентабельность) проекта показатели MNPV и MIRR. Если данных о ставках нет, то NV и IRR и, если есть только ставка дисконта, то NPV и DPI.
Рецензенты:
Сумин В.И., д.т.н., профессор, профессор кафедры управления и информационно-технического обеспечения Федерального казенного образовательного учреждения высшего профессионального образования «Воронежский институт Федеральной службы исполнения наказаний», г. Воронеж;
Астахова И.Ф., д.т.н., профессор, профессор кафедры математического обеспечения ЭВМ Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Воронежский государственный университет», г. Воронеж.
Библиографическая ссылка
Крыжановский О.В., Чулюков В.А. СРАВНЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОЦЕНКИ ЭФФЕКТИВНОСТИ ПРОЕКТНЫХ РЕШЕНИЙ // Современные проблемы науки и образования. – 2015. – № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19840 (дата обращения: 24.04.2024).



