Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы

Бейбалаев В.Д.

На основе уравнения Смолуховского-Эйнштейна дается вывод обобщенного уравнения Фокера – Планка в производных дробного порядка. Рассматривается некоторые решения уравнения параболического типа с дифференцированием дробного порядка a, (0 < a <= 1).

Статья в формате PDF

120 KB

Отсутствие адекватных количественных моделей процессов тепломассообмена в многокомпонентных системах со сложной пространственно- временной структурой, для которых характерны эффекты памяти, самоорганизации привело к  тенденции пересмотра основных положений теории тепломассообмена. Одно из направлений связано с использованием принципа локальной неравновесности [1], что позволяет построить более последовательную теорию массопереноса в гетерогенных системах [2]. Другие направления связаны с использованием методов фликер-шума [3], детерминированного хаоса [4], концепции фрактала [5]. 

Одним из эффективных методов исследования процессов тепломассопереноса является метод основанный на применении стохастических дифференциальных уравнений [6]. В настоящей статье выводятся обобщенные уравнения Фокера-Планка в производых дробого порядка на основе  уравнения Смолуховского-Эйнштейна. Рассматриваются решения некоторых частных случаев обобщенного уравнения Фокера-Планка и их приложения к теории теплопроводости. фильтрации в пористых средах с фрактальной структурой.

Значительные успехи при рассмотрении кинетических явлений  в системах с фрактальной структурой связаны с использованием формализма интегродифференцирования дробного порядка .  Повышенный интерес к дифференциальным уравнениям  дробного порядка [7-9] обусловлено  их физической интерпретацией [10] . Было показано, что переход к производной дробного порядка по времени позволяет учитывать эффекты памяти системы [10]. Это и вызвало  их широкое применение в механике, физике, биофизике экономике - практически во всех областях естествознания [11-16].

Область применимости решений дифференциальных уравнений дробного порядка значительно шире, чем дифференциальных уравнений с целочисленным дифференцированием, поскольку последние оказываются их частным случаем.  Уравнения в производных дробного порядка, позволяют учесть процессы, в которых одновременно участвуют как обратимые, так и необратимые процессы [10,11]. Это позволяет не только получить принципиально новые результаты, но более глубоко осмыслить известные результаты, позволяя при этом, создать адекватные количественные модели исследуемых явлений

1. Обобщенное уравнение Фокера-Планка

В основе описания случайных процессов лежит уравнение Смолуховского-Эйнштейна, которое записывается для условной плотности вероятности имеет вид

[6]

                  (1)

Для вывода обобщенного уравнения Фокера-Планка исходим из выражения

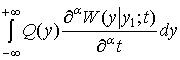                         (2)

где , производная дробного  порядка определена соотношением  [7]

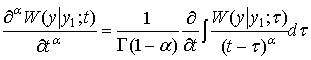                        (3)

Здесь Г(z) - гамма-функция Эйлера. С помощью соотношений (2), (3)  уравнение Смолуховского- Эйнштейна  (1) можно привести к виду

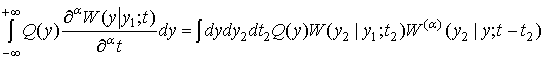 (4)

где введена функция

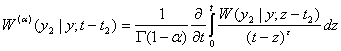
В дальнейшем мы воспользуемся   разложением функции  в обобщенный ряд Тейлора  [7]

где . В результате  уравнение (4) можно привести к виду

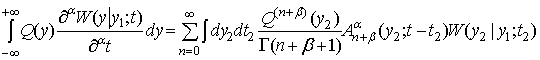(5)

где введены функции

                      (6)

Функции  - представляют собой обобщенные моменты. При  и  (6) переходит в обычное выражение для момента. В  (6), произведя интегрирование по частям,  окончательно получим следующее  дифференциальное уравнение в производных дробного порядка

  (7)

Уравнение (7) представляет собой обобщенное уравнение  Фокера-Планка записанное в производных дробного порядка. Обобщенное уравнение Фокера-Планка (7) позволяет исследовать новый класс стохастических процессов, которые реализуются в системах с фрактальной структурой.

В дальнейшем рассмотрим различные модификации уравнения (7). В частности, предполагая, что для обобщенных моментов справедливо выражение

получим следующее уравнение

      (8)

В случае  и   уравнение (7) переходит в известное уравнение Фокера-Планка [6]. Таким образом, уравнение (7)  представляет собой обобщенное уравнение Фокера-Планка.

Уравнение типа (7) лежит в основе различных задач тепломассопереноса. Уравнения типа (8) используются  при исследовании задач тепломассопереноса.

1. В качестве применения уравнений типа (8)  рассмотрим обобщенное  уравнение теплопроводности  [17 ]

где , ,  - безразмерные время и координата,  - характерные временной и масштабный параметры,  - коэффициент температуропроводности.

Приложение уравнения обобщенной теплопроводности к задачам теории теплового поля земли в рамках концепции фрактала рассмотрено в работе. В частности в случае стационарного поля для распределения температуры в глубь земли получаем следующий результат .

Таким образом, распределение температуры имеет нелинейный характер. 

2. Рассмотрим частный случай  дифференциального  уравнения

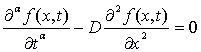                                  (9)

где .

В качестве функции   может быть рассмотрена температура при рассмотрении задач теплопроводности, концентрация вещества при рассмотрении задач массопереноса [18], и распределения давления  при рассмотрении задач гидродинамики [15 ].Решение уравнения  зависит от вида начальных условий. Рассмотрим случай, когда  начальное условие к уравнению (1) дается в виде

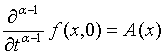                                            (10)

Задачу Коши (9),(10)  решаем, совершая преобразование Фурье по переменной  х

В результате уравнение (9) запишется в виде

решение которого, с начальным условием   известно [7]

Здесь   - функция Миттаг-Леффлера [7].

Отметим, что для целых  функцию Миттаг-Леффлера можно свести к гипергеометрическому ряду. Например, при =k=1,2,...n получим

где  гипергеометрическая функция

Для определения исходной функции, совершая обратно преобразование Фурье, окончательно получим

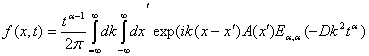                          (11)

Для -источника  и при =1 решение (11)  учитывая, что , принимает известный вид

                                                   (12)

В остальных случая мы имеем новый класс решений.

В случае, например  =1/2, 1/4  функция  принимает вид

Рассмотрим решение уравнения (7) когда задается начальное значение функции . В этом случае удобно использовать преобразование Лапласа. При использовании преобразования Лапласа существенно то, что в отличие от обыкновенной производной, когда имеет место соотношение

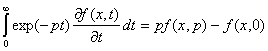
для дробной производной, как можно непосредственно убедиться имеет место соотношение 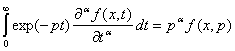.  Для учета начального условия  необходимо его явно внести в уравнение и исходить из уравнения следующего вида [19]

                                    (13)

Второе слагаемое в (13), по существу, есть результат действия дробной производной на начальное условие. Совершая, как и ранее сначала преобразование Фурье по переменной x и, затем преобразование Лапласа по переменной t получим для f(k,p) следующее выражение

что дает для искомой функции следующий результат           

Рассмотрим случай, когда  тогда

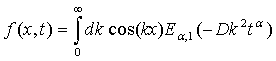                            (14)

При  решения (8) и (12) совпадают. Однако для остальных значений ( ) эти решения существенно отличаются.  Так,  в отличие от решения (8) в (12) отсутствует сингулярный множитель , а также отличается второй индекс функции Миттаг-Леффлера  ( ). В этом случае имеем следующие выражения  функции Миттаг-Леффлера , например, для   :

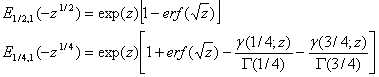
где - неполная Гамма-функция. Характер решения (10) качественно не отличается от решения  (5). Остановимся на решении задачи

                   (15)

для ограниченной области: , с  краевыми условиями

   при х=0                              (16)

     при x=

Эта задача для краевых условий первого рода рассмотрена в работе [20].

Используя метод разделения переменных окончательно получим следующее решение задачи (15,16)

                   (17 )

где,            .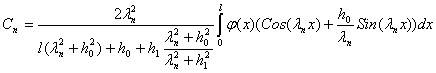

Здесь  корни уравнения

Решение (17) при  совпадает с известным ранее решением . В случае   принимает вид

           (18 )

Поведение решения (14)  при  имеет степенной характер [14]     

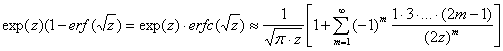
Это отличается от асимптотического поведения решения (12) который имеет экспоненциальный характер.

Полученные решения могут быть использованы при исследовании процессов тепломассопереноса  в системах обладающих фрактальной структурой.

СПИСОК ЛИТЕРАТУРЫ:

1. Соболев С.А. // Усп. физ. наук. 1997. Т.167. № 10. С. 1095.
2. Абаржи И.И.  // Журн. физ. химии. 1999. Т.73. №11. С.1943.
3. Тимашев С.Ф. //Российский хим. журн. 1997. Т.41. № 9. С.17.
4. П.Берже, И.Помо, К.Видаль . Порядок в хаосе. М.:Мир, 1991. 368 с.
5. Олемской А.И., Флат А.Я //Усп. физ.наук.1993.Т.163. №12.С.1.
6. Гарднер К.В. Стохастические методы в естественных науках. М.:Мир. - 1986. 528 с.
7. Самко C.Г., Килбас Ф.Ф., Маричев О.И. Интегралы и производные дробного  порядка   и некоторые приложения. Минск. Наука и техника. 1987.688 с.
8. Oldham K.B., Spanier J. The fractional calculus. New York .1974.234 р.
9. Нахушев А.М. Элементы дробного исчисления и их применение// Нальчик. Изд-во КБНЦ РАН, 2000. - 299 с
10. Нигматулин Р.И.  Дробный интеграл и его физическая интерпретация  //ТМФ. 1992. Т.90,  №3. С. 354-368.
11. Батунин А.В. Фрактальный анализ и универсальность Фейгенбаума в физике андронов //УФН.1995. Т.165, № 6. С. 645-660.
12. Зосимов В.В., Лямшев Л.М. Континуальное описание аномальной диффузии по гребешковой структуре // 1995. Т.166, № 4. С. 361 - 402.
13. Мейланов Р.П. К теории фильтрации в пористых средах с фрактальной структурой //Письма ЖТФ. 1996.Т.22, № 23. С.40-43.
14. Нахушев А.М. Уравнения математической биологии//М.: Высш. шк., 1995.- 301 с.
15. Мейланов Р.П. Обобщенное уравнение одномерной фильтрации с дифференцированиеми дробного порядка //ИФЖ.2001. Т.74, № 2. С. 34-37.
16. Мейланов Р.П., Янполов М.С.Особенности фазовой траектории «фрактального» осциллятора //Письма в ЖТФ. Т.28, №1.С.67-73.
17. Мейланов Р.П. Концепция фрактала в теории теплового поля земли.//Международная конференция «Тепловое поле Земли» Москва 2000 г.  С. 63-68.
18. Р.П.Мейланов, Д.А. Свешникова, О.М. Шабанов.//ЖФХ. 2003, Т.77,№ 3, С. 260-264.
19. Кочубей А.Н. Диффузия дробного порядка // ДУ 1990. Т.26, № 4. - С .660 - 670
20. Геккиева С.Х. Краевая задача для обобщенного уравнения переноса с дробной производной по времени //Доклады Адыгской АН. 1994. Т.1,№ 1. С.17-18

Библиографическая ссылка