Оптимальную структуру изучения и применения математического материала студентами-экологами можно наглядно представить в виде следующей схемы:
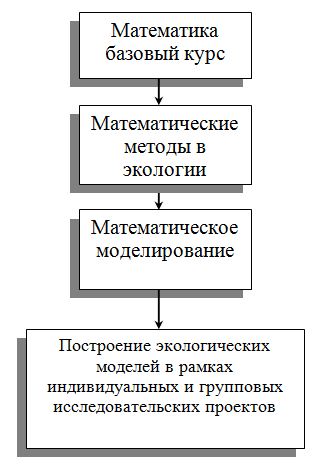
В соответствии с приведенной схемой, фундаментом математической подготовки будущего эколога является базовый курс математики, на основе которого строятся все остальные блоки. При этом с каждой новой ступенью знакомства с математическими методами на передний план все больше «выходят» потребности специальных дисциплин. При этом попутно происходит закрепление, конкретизация, расширение и углубление уже усвоенных математических знаний и навыков студентов, которые ложатся в основу математического аппарата, непосредственно используемого при решении экологических проблем различного характера.
Вполне очевидно, что основным фактором, определяющим характер математического содержания обучения студентов, являются особенности их будущей профессиональной деятельности. Причем требования со стороны профессиональной деятельности задает контекстный принцип построения не только отдельных дисциплин, но и содержания всей подготовки специалиста в вузе, выступая как системообразующий фактор, под влиянием которого в процессе учебно-профессиональной деятельности происходит не только передача и усвоение информации, но и моделирование тех или иных компонентов будущей профессиональной деятельности.
Учитывая сказанное, мы строим математическую подготовку студентов экологических специальностей на основе принципов [1, 5, 6]: опоры на изученные ранее математические разделы, контекстности, в соответствии с которыми математическая деятельность должна моделировать соответствующий компонент реальной профессиональной деятельности специалиста-эколога, и творческой активности, предполагающие не только непосредственную реализацию известных математических процедур, но и некоторые элементы экологического исследования. В качестве основного средства, обеспечивающего преемственность подготовки будущих экологов применительно к математическому материалу, рассматриваются математические задачи различной степени профессиональной значимости.
Углубленный анализ рабочих программ и опрос преподавателей специальных и общепрофессиональных дисциплин позволили нам выявить по каждому разделу курса математики состав умений и навыков, используемых в специальной подготовке студентов-экологов, что нашло свое адекватное отражение в составленной нами учебной программе курса математики для экологов.
Так, например, в специальной подготовке студентов-экологов широко востребован материал теории матриц и определителей при проверке условий устойчивости равновесного состояния взаимодействующих популяций, характерных для большинства природных и лабораторных популяций. Соответствующий математический раздел «Элементы линейной алгебры», включающий в себя упомянутую теорию, изучается в первом семестре, когда специальные знания студентов еще не являются глубокими и всесторонними, в то время как математические закономерности должны быть им уже достаточно понятны. Проиллюстрируем сказанное на следующем примере:
Пример. Для исследования устойчивости состояния равновесия x1=0, х2=0, x3 = 0 системы
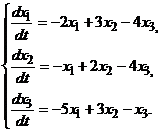 (3.14)
(3.14)
найдите собственные значения матрицы составленной из коэффициентов при переменных 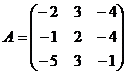 этой системы.
этой системы.
При рассмотрении подобных примеров «опережающая» демонстрация возможностей математических методов исследования естественнонаучных и прикладных проблем при сохранении логической структуры и строгости изложения предмета позволяет добиться того, что абстрактность математических понятий и методов исследования будет восприниматься студентами как естественный прием изучения реальных явлений. В свою очередь, повышение у студентов интереса к изучению основ математической науки, появление у них четких мотивационных установок к учебно-познавательной деятельности позволяет существенно повысить качество усвоения математического содержания.
На следующем этапе при изучении курса «Математические методы в экологии» представления студентов-экологов о значимости математики для будущей профессиональной деятельности дополняются умениями использования математико-статистического аппарата обработки результатов экспериментальных исследований. Рассмотрим в качестве примера исследование закономерности варьирования признака Х: «содержание кальция в сыворотке крови обезьян», по данным анализа биопроб, для проведения которого необходимо использовать биометрию - науку, позволяющую обрабатывать и анализировать экспериментально полученные данные на основе совокупности математических методов, применяемых в биологии и заимствованных из области математической статистики и теории вероятности [4].
Обработка начинается с упорядочения или систематизации собранных данных в виде вариационного ряда (в зависимости от того, как варьирует признак - дискретно или непрерывно, в широком или узком диапазоне, - статистическая совокупность распределяется в безынтервальный или интервальный вариационные ряды) и графического их представления. Нахождение средних величин (средняя арифметическая 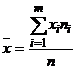 , мода М0, медиана Ме), показателей вариации (вариационный размах R=xmax-xmin, дисперсия
, мода М0, медиана Ме), показателей вариации (вариационный размах R=xmax-xmin, дисперсия 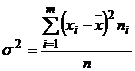 , среднеквадратическое отклонение
, среднеквадратическое отклонение ![]() , коэффициент вариации
, коэффициент вариации ![]() ), коэффициента асимметрии (
), коэффициента асимметрии (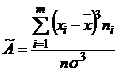 ) и эксцесса (
) и эксцесса ( 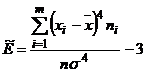 ) позволит в полной мере оценить изменчивость признака.
) позволит в полной мере оценить изменчивость признака.
Вполне очевидно, что привлечение подобных примеров существенно усилит математический компонент профессиональной подготовки студентов-экологов, приучая их к обязательному математико-статистическому обоснованию формулируемых экспериментальных гипотез.
Интеграция метода моделирования явлений и процессов, имеющих место в экологической практике, и математико-статистического аппарата характерна для завершающих этапов математической подготовки будущих экологов, на которых ведущей деятельностью становится подготовка индивидуальных и групповых экологических проектов, реализуемых в рамках научно-исследовательской работы студентов.
Укажем в качестве примера проект утилизации промышленных отходов в составе строительных композиционных материалов, который позволяет решить две задачи: существенно снизить себестоимость строительных материалов, а также в определенной степени решить проблему захоронения отходов [3].
При этом на использование отходов накладывается ряд ограничений. В первую очередь, это касается их экологической безопасности. Во-вторых, необходимо произвести оценку экономической эффективности применения и выявить направление использования отхода, определив его химико-минералогический состав и агрегатное состояние.
Одним из основных параметров работоспособности материалов, как известно, является их долговечность. Согласно кинетической концепции прочности, долговечность описывается выражением: ![]() , где U0 - максимальная энергия активации разрушения, γ - структурно-механический фактор, Тт - предельная температура существования материала - физические константы материала; R - универсальная газовая постоянная; Т - температура, σ - напряжение.
, где U0 - максимальная энергия активации разрушения, γ - структурно-механический фактор, Тт - предельная температура существования материала - физические константы материала; R - универсальная газовая постоянная; Т - температура, σ - напряжение.
В рассматриваемом случае знания, умения и навыки, полученные студентами при изучении функционального анализа, и, в частности, знание свойств и графика функции y=ex, умение работать с графиками основных элементарных функций, позволяют им более глубоко исследовать длительную прочность эпоксидных композитов, на этой основе рассмотреть возможность использования строительных отходов, входящих в состав строительных композитов, и, как следствие, добиться значительной экономии за счет снижения себестоимости при сохранении высокого качества материалов.
Наш опыт преподавания свидетельствует о том, что предложенные педагогические решения доступны для студентов экологических специальностей вузов и при этом позволяют существенно фундаментализировать их профессиональную подготовку как за счет усиления роли математического моделирования, так и посредством целенаправленного придания различным видам учебной математической деятельности будущих экологов профессионально значимого характера.
Рецензенты:
- Найниш Лариса Алексеевна, д.п.н., профессор, заведующий кафедрой начертательной геометрии и графики, Пензенский государственный университет архитектуры и строительства Министерства образования и науки РФ, г. Пенза.
- Голованов Олег Александрович, д.ф.-м.н., профессор, профессор кафедры общепрофессиональных дисциплин, Военный учебно-научный центр Сухопутных войск «Общевойсковая академия Вооруженных сил Российской Федерации» (филиал), г. Пенза.
Библиографическая ссылка
Родионов М.А., Мазей Ю.А. СОДЕРЖАТЕЛЬНО-ПЕДАГОГИЧЕСКИЕ ОСОБЕННОСТИ ПРОФЕССИОНАЛЬНО ОРИЕНТИРОВАННОГО ОБУЧЕНИЯ МАТЕМАТИКЕ СТУДЕНТОВ ЭКОЛОГИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ // Современные проблемы науки и образования. – 2012. – № 2. ;URL: https://science-education.ru/ru/article/view?id=5960 (дата обращения: 20.04.2024).



