Для изучения этого вопроса была рассмотрена схема рабочего процесса раздачи жидких кормов по горизонтальному желобу трапециидальной формы поперечного сечения с наклоном стенок в 450. Жидкий корм из емкости после открытия затвора самотеком поступает в желоб и перемещается под действием естественного напора с высотой столба Z0 = H по длине желоба.
По технологическим соображениям, для достижения минимума затрат материалов и энергии, высота емкости принимается не более 1 м. Атмосферное давление одинаково и в емкости, и в самом желобе, поэтому напора равного 1 метру недостаточно для движения жидкого корма на большие расстояния, например, до 75 метров. Вращающаяся в желобе пружина с шагом s, примерно, равным диаметру пружины D, служит лишь для создания небольшого напора с целью обеспечения гидравлического уклона i, другими словами для компенсирования гидравлических потерь по длине желоба.
При перемещении материала винтовой поверхностью, пружина укорачивается, поэтому на противоположном от привода конце пружины устанавливается упорное подшипниковое устройство.
Конструктивные параметры пружинно-транспортирующего рабочего органа подбираются для компенсации потерь, так как вращающаяся пружина в данном случае выступает в роли насоса, создающего соответствующее давление в желобе. Давление создаваемое вращающейся пружиной увеличивается пропорционально его длине и частоте вращения.
Уравнение Бернулли относительно плоскости, проведенный через нижнюю точку живого сечения имеет вид:
![]() , (1)
, (1)
где α – коэффициент кинетической энергии (Кориолиса);
P0 = Pатм –внешнее давление; h – наибольшая глубина потока.
Учитывая, что (v+dv)2 =v2 + 2vdv + (dv)2 находим:
![]() (2)
(2)
Известно, что ![]() и (dv)2 → 0 сокращая в левой и правой части уравнения (2) слагаемые h,
и (dv)2 → 0 сокращая в левой и правой части уравнения (2) слагаемые h, ![]() ,
, ![]() находим:
находим:
![]() (3)
(3)
В случае перемещения жидких кормов по желобу с вращающейся пружиной уравнение (3) запишется в виде:
![]() (4)
(4)
Для нахождения напора, создаваемого пружиной ![]() , рассмотрим задачу о распределении давления на вязкую жидкость вдоль горизонтального желоба при вращении в ней пружины.
, рассмотрим задачу о распределении давления на вязкую жидкость вдоль горизонтального желоба при вращении в ней пружины.
Пружина средним радиусом ![]() вращается с угловой скоростью
вращается с угловой скоростью ![]() , и движется вдоль трубы с линейной скоростью
, и движется вдоль трубы с линейной скоростью ![]() Диаметр про волоки пружины обозначим
Диаметр про волоки пружины обозначим ![]() , ход винта - s, плотность жидкости -
, ход винта - s, плотность жидкости - ![]() , ее кинематическая вязкость -
, ее кинематическая вязкость - ![]() .
.
Сила, действующая на жидкость со стороны одного витка проволочного винта, равна лобовому сопротивлению обтекающего его потока и вызывается разностью давлений по обе стороны потока и напряжениями трения:
![]() . (5)
. (5)
Перепад давления по потоку, обтекающего виток проволоки, определяется по формуле:![]() , в которую подставляется относительная скорость смеси
, в которую подставляется относительная скорость смеси ![]() , и коэффициент сопротивления
, и коэффициент сопротивления ![]() .
.
В случае движения жидкости и проволочного винта в канале скорость перемещения жидкости относительно пружины ![]()
![]() где
где ![]() – линейная осевая скорость движения проволочного винта, а
– линейная осевая скорость движения проволочного винта, а ![]() – осевая скорость жидкости относительно канала.
– осевая скорость жидкости относительно канала.
Запишем уравнение Бернулли для объема соответствующего шагу винта ![]() вдоль оси
вдоль оси ![]() .
.![]()
Умножив на число витков вдоль трубы ![]() , получим значение напора в конце желоба:
, получим значение напора в конце желоба:
![]() . Если
. Если ![]() , тогда
, тогда
![]() . (6)
. (6)
А элемент напора, создаваемого пружиной ![]() будет равен:
будет равен:
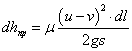 . (7)
. (7)
Подставляя (7) в (4) получим выражение, позволяющее определить влияние различных параметров на перемещение корма по желобу:
![]() . (8)
. (8)
В случае перемещения вязкой жидкости без уклона, равномерно и при ![]() , получим зависимость:
, получим зависимость:
![]() . (9)
. (9)
Из этого выражения можно определить скорость перемещения вязкой жидкости в зависимости от скорости вращения и конструктивных параметров пружины и свойств жидкости:
![]()
Обозначим ![]() , получим
, получим
![]() . (10)
. (10)
В случае, когда i = 0, а потери напора ![]() , тогда уравнение Бернулли запишется:
, тогда уравнение Бернулли запишется:
![]() (11)
(11)
Тогда, подставив значение перепада давления из-за вращения пружины из формулы:
![]() , (12)
, (12)
в уравнение (17), получим уравнение для определения осевой скорости жидкости:
![]() (13)
(13)
Приведем его к виду, удобному для решения, и получим квадратное уравнение относительно ![]() :
:
![]() . (14)
. (14)
где ![]() . Дискриминант этого уравнения равен:
. Дискриминант этого уравнения равен:
![]() =0.
=0.
Величина дискриминанта положительна D>0 только при ![]() =0. В этом случае линейная скорость движения должна удовлетворять неравенству:
=0. В этом случае линейная скорость движения должна удовлетворять неравенству:
![]() =0.
=0.
Далее, решая это квадратное уравнение, получаем значение скорости движения жидкости по желобу:
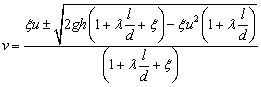 . (15)
. (15)
Знак выбирается из физических условий, чтобы скорость движения была положительной.
Для жидкости с плотностью ![]() = 1200кг/м3 и вязкостью
= 1200кг/м3 и вязкостью ![]() м2/с наблюдается удовлетворительное совпадение результатов эксперимента с теоретической зависимостью
м2/с наблюдается удовлетворительное совпадение результатов эксперимента с теоретической зависимостью ![]() . Совпадение результатов эксперимента с теоретической зависимостью подтверждает механизм движения жидкости в сложных условиях вращения проволочного винта в желобе, позволяет использовать полученные в работе данные при разработке и конструировании, устройств и агрегатов для транспортировки различных жидкостей при помощи спирально–винтовой пружины.
. Совпадение результатов эксперимента с теоретической зависимостью подтверждает механизм движения жидкости в сложных условиях вращения проволочного винта в желобе, позволяет использовать полученные в работе данные при разработке и конструировании, устройств и агрегатов для транспортировки различных жидкостей при помощи спирально–винтовой пружины.
Библиографическая ссылка
Исаев Ю.М. ТЕХНОЛОГИИ ПЕРЕМЕЩЕНИЯ ЖИДКИХ КОРМОВ ПРУЖИННЫМ ТРАНСПОРТЕРОМ // Современные проблемы науки и образования. – 2006. – № 6. ;URL: https://science-education.ru/ru/article/view?id=642 (дата обращения: 24.04.2024).



