Введение
Ввиду многообразия процессов человеческой деятельности человек часто сталкивается с ситуацией, когда он вынужден иметь контакт с горячими или холодными объектами. Обычно такие ситуации возникают при тушении пожаров, на производстве сталелитейной промышленности, связанной с переработкой и получением металлов и сплавов, при работе в экстремальных морозных условиях, а также при эксплуатации криогенных систем. Кроме того, адекватные ситуации могут возникнуть, когда температура окружающей среды превышает 45 °С. Последнее вызывает денатурацию белка, то есть ожог, а, следовательно, боль, как некомфортное ощущение. Человек старается различными способами оградить себя от таких воздействий, например путём применения специальной одежды, которую промышленность изготавливает для работников пожарных служб, МЧС, рабочих металлургических цехов и др.
Обычно специализированная одежда состоит из нескольких слоёв разных по функциональному назначению материалов, при этом максимально удовлетворяются критерии высокого качества и экономичности.
В связи с изложенным весьма актуальным становится аналитическое решение теплотехнической задачи нестационарной теплопроводности двух полубесконечных неизотермических тел, находящихся в кратковременном контакте. При этом одно из тел имеет тонкое покрытие.
В дальнейшем при проведении анализа будем рассматривать одежду в качестве покрытия, а два неизотермических полубесконечных тела представляют кожу МБО и горячий (холодный) объект.
В качестве постановки задачи рассмотрим вариант кратковременного контакта субъекта в специализированном одеянии с холодным объектом. Анализ будем проводить с позиции комфортного ощущения поверхностной ткани человека (кожи) и плотно прилегающей к ней одежды. Такая ситуация, например, реализуется, когда человек перемещается из помещения с комнатной температурой во внешнюю среду с пониженной температурой, в которой находящиеся объекты имеют одинаковую температуру.
В такой постановке предложенная физическая модель имеет своей целью установить не только верхнюю границу зоны комфорта (температуру ожога), но и нижнюю границу зоны комфорта (температуру выше температуры кристаллизации тканей и температуры некроза).
Материалы и методы.
Итак, в работе анализируется система из двух полуограниченных неизотермических тел, находящихся в непродолжительном контакте, одно из которых имеет тонкое покрытие (рис. 1).
Представленная выше физическая модель может быть описана следующей математической моделью. В начальный момент времени τ = 0 (τ ≥ 0) покрытие и первое тело имеют одинаковую температуру ![]() . Для такого случая система дифференциальных уравнений нестационарной теплопроводности имеет вид:
. Для такого случая система дифференциальных уравнений нестационарной теплопроводности имеет вид:
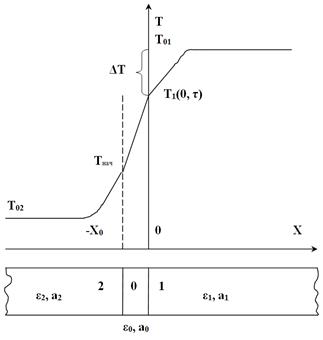
Рис. 1. Температурное поле полуограниченного тела с кожей человека с плотно прилегающей одеждой. ε –коэффициент тепловой (термической) активности материала, а – коэффициент температуропроводности материала. 1 и индексом 1 обозначается тело (горячее или холодное), с которым контактирует МБО; 2 и индексом 2 обозначается МБО; 0 и индексом 0 обозначается покрытие, которое моделируется как слой ткани одежды.
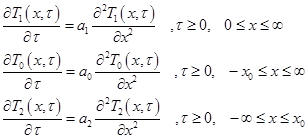 (1)
(1)
При начальном условии:
![]() ,
,
![]()
и граничных условиях:
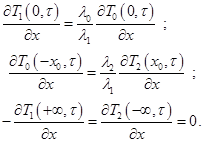
Как известно, тепловая (термическая) активность материалов представляется соотношением вида: ε2=λ∙Ср∙ρ, где λ - коэффициент теплопроводности материала (Вт/(м∙К)), Ср - коэффициент теплоёмкости материала при постоянном давлении (Дж/К), ρ - плотность материала (кг/м3).
Пределы применимости рассматриваемой модели (1) связаны с выполнением следующих основных условий: время введения в контакт с нагретым телом должно быть заметно меньше длительности соприкосновения; длина диффузии температурного поля в каждую из сред должна быть заметно меньше линейного размера, характеризующего толщину тела по вектору распространения теплового потока в месте контакта; вместе с тем эта длина не должна превышать протяженность (толщину) соприкасаемых тел. В модели пренебрегается неоднородностью кожного покрова и циркуляцией в нем крови.
Используя преобразования Лапласа, решение основного дифференциального уравнения теплопроводности в форме для координаты х=0 представляется в виде:
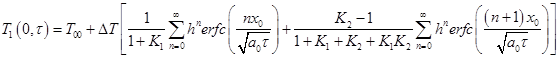 (2)
(2)
где: ![]() , n
, n![]() Z
Z![]() Z
Z![]() [0;∞).
[0;∞).
х0 - толщина покрытия, моделируемая тканью одежды.
При τ→0 или х0→∞ из (2) получим:
![]() (3)
(3)
При τ→∞ или х0→0 из (2) получим:
![]() (4)
(4)
В этом легко убедиться, если принять х0=0, то функции 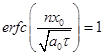 и
и 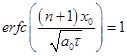 , сумма
, сумма![]() . Подставляя эти соотношения в формулу (2) получим формулу (3). Аналогично, при х0=∞ получим
. Подставляя эти соотношения в формулу (2) получим формулу (3). Аналогично, при х0=∞ получим 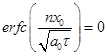 и
и 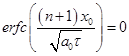 , и выражения можно записать так:
, и выражения можно записать так: 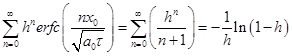 и
и 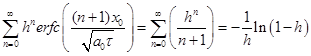 . Подставляя эти соотношения в формулу (2) получим формулу (4). Видно, что уравнение (3) и (4) совпадает с решением задачи для двух тел, имеющих коэффициенты тепловой активности
. Подставляя эти соотношения в формулу (2) получим формулу (4). Видно, что уравнение (3) и (4) совпадает с решением задачи для двух тел, имеющих коэффициенты тепловой активности ![]() и
и ![]() или
или ![]() и, соответственно, приведённых в контакт. Это очевидно из физического смысла постановки задачи (1).
и, соответственно, приведённых в контакт. Это очевидно из физического смысла постановки задачи (1).
Анализ результатов
Проанализируем соотношение (2) для различных возможных вариантов контактирующих тел. Цель анализа сводится к определению толщин хi покрытий (одежды), при которых человек может получить ожог. Анализ проведён для кожи человека (ε =1100 Дж/м2·К·с0,5) при максимальном уровне допустимой температуры Т1(х,0) = 45 °С (температура ожога). При этом рассматривались три рода разных тел, контактирующих с одеждой человека (покрытием): металл с тепловой активностью для них εмет = 10 000 Дж/(м2·К·с0,5), пластмасса с εпл = 2000 Дж/(м2·К·с0,5) и хлопок с εхл = 200 Дж/(м2·К·с0,5). Причём в качестве покрытия рассматривалась хлопковая ткань. Температуропроводность принималась везде одинаковая а1=а2=а0=1,6*10-7 м2/с. Результаты анализа представлены на рисунке 2.
Решением уравнения (2) является поверхность в пространственных координатах времени контакта t (c), температуры Т (°С) в плоскости соприкосновения двух тел (х=0) и толщины покрытия х0 (м). Для более наглядного представления зависимости толщины покрытия от времени контакта трёхмерный график плоскости отобразим в виде проекции его на плоскость О(х0, t). Цветовой гаммой выделим уровни температуры от 37 до 100 °С. Цветовая гамма меняется при изменении температуры порядка 10 °С. Так, например, красный цвет соответствует температуре 90 °С, а трудно заметный фиолетовый – 37 °С, следующий за фиолетовым цветом – тёмно-синий – соответствует температуре в 45 °С.
Более подробно о теплофизических свойствах различных веществ и материалов можно найти в различных справочниках, включая электронные аналитические и отраслевые [1-3]. Наиболее характерные примеры приведены в таблице 1. Средним диапазоном комфортных температур является отрезок [29; 37] °С [4].
а)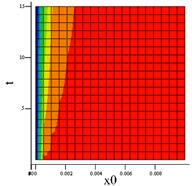 б)
б)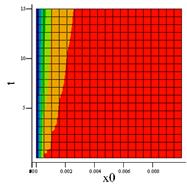 в)
в)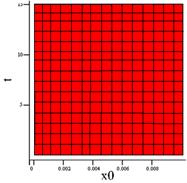
Рис. 2. Проекция трёхмерного графика уравнения (2) на плоскость О(х0, t). а) εмет = 10000 Дж/(м2·К·с0,5) при температуре 100 °С; б) εпл = 2000 Дж/(м2·К·с0,5) при температуре 100 °С; в) εхл = 200 Дж/(м2·К·с0,5) при температуре 100 °С.
Таблица 1
|
Материал |
Тепловая активность, Дж/(м2·К·с0,5) |
|
Пушистые, мягкие предметы (мех, вата, хлопок) |
10-50 |
|
Лёгкие пористые тела (поролон, пенопласт) |
100-250 |
|
Дерево |
300-900 |
|
Органические жидкости |
400-900 |
|
Натуральная кожа |
200-300 |
|
Пластмассы |
500-2000 |
|
Стекло |
1300-1800 |
|
Вода |
1570 |
|
Металлы |
10 000-30 000 |
|
Кирпич |
900-1150 |
|
Стеклопластик (существует изотропия) |
800-950 |
|
Углепластик (существует изотропия) |
1200-4000 |
|
Цемент |
1400 |
|
Кожа МБО |
800-1200 |
При компьютерном расчёте в среде Mathcad 13 для моделирования ситуации контакта с телами, имеющими малую тепловую активность (рис. 2в) получены одинаковые графики распределения температур при 15 с и при 150 с, в обоих случаях температура постоянна и равна 90 °С независимо от толщины подложки.
Отсюда следует, что для изготовления одежды, защищающей от высоких температур, необходимо её производить из комбинированных материалов, с минимальной тепловой активностью. Причём для экономии материалов и сокращения толщины одежды (покрытия) достаточно слои делать минимальной толщиной. Однако это вызовет снижение прочности изделия, что недопустимо. Поэтому в перспективе для производства высококачественной спецодежды необходимо совершенствовать технологию изготовления спецматериалов с необходимыми как механическими, так и теплофизическими свойствами. Теплофизическим критерием является многослойность различных материалов с низкой тепловой активностью, плотно прилегающих друг к другу и имеющих минимальную толщину.
Толщина покрытия влияет на температуру в плоскости соприкосновения согласно аналитической формуле (2). Проиллюстрируем это на примере (рис. 3). Задача моделировалась для широкого круга горячих тел с тепловой активностью от 10 до 10 000 Дж/(м2·К·с0,5) и временем соприкосновения 0-150 с. В качестве тела с покрытием выбрано МБО ε(кожи)=1100 Дж/(м2·К·с0,5), а=1,6*10-7 м2/с, а покрытие было с тепловой активностью ε(тела)= 2000 Дж/(м2·К·с0,5). Толщина покрытия принималась 0,001 м и 0,01 м. Для рисунка 3а минимальная температура составила порядка 68 °С, в то время как для рисунка 3б – порядка 90 °С.
А) 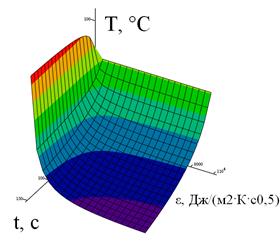 Б)
Б) 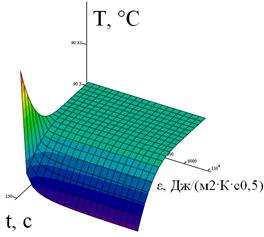
Рис. 3. Зависимость тепловой активности горячего тела от времени соприкосновении при а) х0=0,001 м и б) х0=0,01 м.
Используя литературные данные по теплофизическим свойствам и подставляя в формулу (2), можно получить критерий комфортности для нижней его границы [4]. Так, если смоделировать ситуацию, когда МБО ε(кожи)=1100 Дж/(м2·К·с0,5), а=1,6*10-7 м2/с с покрытием (одеждой) с εхл = 100 Дж/(м2·К·с0,5) при температуре в 37 °С касается тела εпл = 2000 Дж/(м2·К·с0,5) при 10 °С, то моделированием в среде Mathcad 13 получим график зависимости температуры места касания от времени контакта двух тел и толщины покрытия. Максимальная температура достигается порядка 28 °С, в то время как нижний предел зоны комфорта находится в районе 29 °С.
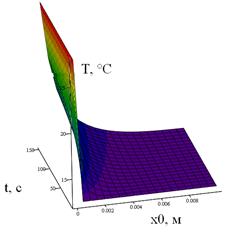
Именно тепловая активность отвечает за температурные ощущения на границе контакта двух тел при кратковременном касании, а не теплопроводность [6]. Так, например, раскалённый докрасна (100-150 °С) пористый материал на основе тонких нитей оксида кварца с тепловой активностью порядка 150-300 Дж/(м2·К·с0,5) и теплопроводностью 0,05-0,25 Дж/(м·К) не вызовет ожог при кратковременном касании.
Выводы
С использованием преобразования Лапласа проведено решение основного дифференциального уравнения теплопроводности для кратковременного контакта двух полуограниченных неизотермических тел, одно из которых имеет покрытие. Показано, что температура в плоскости контакта двух изотермических тел, одно из которых имеет покрытие, зависит от толщины покрытия. Для времён контакта порядка 150 с, согласно аналитическому выражению, при уменьшении толщины покрытия снижается и температура в плоскости соприкосновения тел при прочих равных условиях. Графически дан анализ основного уравнения, полученного в работе, в зависимости от тепловой активности второго тела. В рассматриваемом примере покрытие моделировалось как спецодежда для работников пожарной службы, сталелитейного производства и других. В работе представлена методика оценки толщины одежды с её тепловой активностью, которая способна уберечь кожный покров человека от ожога.
Рецензенты:
Никитин Пётр Васильевич, д.т.н., профессор кафедры «Конструкция и проектирование двигателей» ФГБОУ ВПО «Московский авиационный институт (национальный исследовательский университет)», г. Москва.
Спирин Геннадий Георгиевич, д.т.н., профессор кафедры «Физика» ФГБОУ ВПО «Московский авиационный институт (национальный исследовательский университет)», г. Москва.
Библиографическая ссылка
Симанков Д.С. ВЛИЯНИЕ ПОКРЫТИЯ НА ФОРМИРОВАНИЕ ПОЛЕЙ ТЕМПЕРАТУР ПРИ КРАТКОВРЕМЕННОМ КОНТАКТЕ ДВУХ ПОЛУОГРАНИЧЕННЫХ НЕИЗОТЕРМИЧЕСКИХ ТЕЛ // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=8621 (дата обращения: 19.04.2024).



