Федеральные государственные образовательные стандарты основного общего образования третьего поколения определяют повышенные требования к компьютерной поддержке процесса обучения. В частности, «..предметные результаты изучения предметной области "Математика и информатика" должны отражать: <…> 9) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах; 10) формирование информационной и алгоритмической культуры; формирование представления о компьютере как универсальном устройстве обработки информации; развитие основных навыков и умений использования компьютерных устройств…» [1].
Возможность удовлетворения этому требованию стандарта при обучении геометрии обеспечивается специализированным программным обеспечением – интерактивными геометрическими средами (ИГС): GeoGebra, GeoNext, «Живая математика», «Математический конструктор», а также создаваемыми на основе этого программного обеспечения цифровыми образовательными ресурсами (ЦОР) [2-4]. Достоинством названного программного обеспечения и основанных на нем ЦОР является интерактивность, т.е. возможность не только внесения пользователем начальных данных для построения изображения геометрической конфигурации, но их параметризация с последующим изменением при сохранении общего алгоритма построения чертежа, а также возможность оперативного получения интересующих пользователя сведений о свойствах изображенных фигур. Свойство интерактивности позволяет рассматривать ИГС как виртуальные динамические лаборатории, используемые учащимися для проведения исследований на уроках и во внеурочное время с привлечением эмпирических методов научного познания: наблюдений, опытов, экспериментов.
Проведенный нами ретроспективный анализ школьных учебников геометрии [12; 14] и методических трудов [5-11] показал, что в истории развития представлений о месте эмпирических методов в системе методов обучения геометрии можно условно выделить следующие этапы:
· период дедуктивного изложения школьного курса геометрии сообразно «Началам» Евклида (XVII – конец XVIII в.);
· период обращения к эмпирическим методам как к альтернативе дедуктивного способа изложения (конец XVIII - середина XX в.);
· период полного отказа от обращения к эмпирическим методам познания в обучении геометрии (60–80-е гг. ХХ в.);
· период поиска разумного сочетания эмпирических и теоретических методов в обучении геометрии (конец 90-х гг. XX в. - настоящее время).
Первый период в истории развития представлений о месте эмпирических методов в системе методов обучения геометрии характеризуется влиянием учебника «Начала» Евклида, с его логическим построением курса. «Начала» Евклида в этот период в России переиздается три раза: в 1739 году в переводе И. Сатарова, в 1769 году - Н. Курганова, в 1784 году - В. Никитина и П. Суворова. Пришедшие на смену «Началам» Евклида учебные пособия сохраняли дедуктивный подход к изложению материала, добавляя лишь объяснительный, иллюстративный и задачный материал. К этому периоду можно отнести такие учебные пособия, как «Приемы циркуля и линейки» (1709) (перевод австрийской книги А.Э. Буркгарда фон Пюркенштейна «ErtzherzogUche Handgriffe des Zirckels und Lineals», Wien, 1686), «Краткое руководство к теоретической геометрии» Крафта Г.В. (1762), «Генеральная геометрия» Курганова Н.Г. (1765) и др.
Н.А. Извольский, автор первой советской книги по методике обучения геометрии («Методика геометрии», 1924), говоря об учебных пособиях того периода, отмечал: «И наши наиболее ходовые учебники (Давыдов, Киселев и многие другие, им подражающие), и наша традиционная система преподавания геометрии ... все культивирует взгляд на геометрию, как на собрание теорем. И это обстоятельство является коренным недостатком наших наиболее распространенных учебников» [5, с. 33].
Понимая и признавая эти недостатки дедуктивного подхода к изложению основ геометрии, многие ученые-математики стали искать альтернативный путь развертывания содержания. В связи с этим наряду с классическими учебниками (Киселева А.П., Давыдова А.Ю., Гангуса Р.В. и Гурвица Ю.О. и др.), в которых сохраняется дедуктивный подход, начали появляться и использоваться учебные пособия, основанные на эмпирическом подходе. Их появление и ознаменовало начало второго периода в развитии взглядов ученых на построение школьного курса геометрии. К этому периоду можно с полным правом отнести такие учебные пособия по геометрии, как «Основания геометрии» С.Е. Гурьева (1811), «Наглядная геометрия» М.О. Косинского (1867), «Геометрия на задачах» С.И. Шохора-Троцкого (1908), «Элементарная математика. Геометрия» Э. Бореля по ред. В.Ф. Когана (1911), «Наглядная геометрия» А.М. Астряба (1923), «Учебник геометрии. Курс единой трудовой школы» А.Р. Кулишера (1922) и др. В этих учебниках старая элементарная геометрия в евклидовом понимании отступает назад под влиянием передовых идей, к числу которых относится метод целесообразных задач С.И. Шохора-Троцкого, наглядно-эмпирический подход А.М. Астряба, лабораторного метода А.Р. Кулишера, С.А. Богомолова, эспериментального подхода Н.Д. Мукалова, К.Ф. Лебединцева и др.
Однако полный отказ от дедуктивности в изложении с подменой логических доказательств демонстрациями очевидности формулируемых утверждений в ряде учебников также оказался ущербным. Описывая недостатки таких курсов, Н.А. Извольский [5, с. 10] отмечал: «На протяжении всего курса учащимся предлагают проделать целый ряд опытов (вроде: возьми циркулем такой-то отрезок и сравни его с таким-то, - убедись из этого, что первый отрезок в 2 раза меньше второго; или: вырежь из бумаги такие-то треугольники, наложи их один на другой и убедись, что они равны и т.п.), из которых учащиеся должны убедиться в справедливости того или иного геометрического предложения <…> опыт, сам по себе, убедить в непреложности какого-либо геометрического свойства не может; его роль сводится лишь к тому, что благодаря ему в некоторых случаях (и далеко не часто) возникает потребность выполнить ту или иную геометрическую работу, а эта последняя приводит иногда к установлению непреложности известного свойства. <…> Cказать, что нужны наглядные доказательства, основанные на интуиции, опыте и т.п. - слишком мало; должно было присоединить сюда ряд примеров, где бы отчетливо выяснялось бы, как именно можно использовать опыт, чтобы благодаря ему сделать ясной необходимость известного свойства» [5, с. 22].
Приведенная цитата показывает, что Н.А. Извольский считал использование опыта для обоснования истинности формулируемых утверждений общего характера «грубым», не соответствующим логике развития содержания геометрии. И в этом он был совершенно прав, так как даже в период становления геометрии устанавливаемые в ней эмпирические зависимости основывались на обобщении результатов множественных опытов и подкреплялись абстрактными рассуждениями. Более корректным, с его точки зрения, было бы обращение не к одиночным испытаниям, а к методу эксперимента. Экспериментальный метод, в отличие от опыта, мыслился как серия опытов над выборочной совокупностью геометрических объектов, сформированной в соответствии с принципом репрезентативности выборки, т.е. правильности представления ею генеральной совокупности.
Экспериментальный метод обучения впервые был введен в систему преподавания физико-математических дисциплин академической гимназии в конце XVIII в. М.В. Ломоносовым. В методике обучения математике экспериментальный метод стал предметом изучения лишь с начала XIX века. (Л.В. Глаголева, П.Д. Енько, Н.Д. Мукалов). Учеными стали осмысливаться образовательные функции данного метода, уточняться его место в системе методов обучения математике, описываться различные учебные разновидности и организационные формы проведения экспериментов.
Так, к примеру, Н.Д. Мукалов описывал значение экспериментального метода при обучении математике: «учитель показывает учащимся предметы, подлежащие рассмотрению, ученики же под руководством учителя проделывают самостоятельные опыты, построения и т.д. и таким путем приводятся к необходимым выводам. Здесь дети активно участвуют в работе; они при этом приобретают самостоятельные навыки, и приобретенные таким путем знания прочно запечатлеваются в уме учащихся. Кроме того, такого рода занятия составляют для детей громадный интерес, так как ими представляется детям постоянная деятельность, к которой они по своей природе всегда стремятся» [6, с. 6].
За экспериментальным методом, применяемым для целей обучения, постепенно закрепился термин «лабораторный метод», который не только указывал на способ учебного познания, но и на условия реализации этого способа. Стали возникать и термины, обозначающие его разновидности. Так, Лексин Н.Г. в своей книге «Лабораторный метод изучения геометрии» (1916) ввел термин «наглядно-лабораторный метод», раскрывая его смысл следующим образом: «Одного наблюдения, одной поверхностной наглядности ещё недостаточно. Здесь необходима активная работа самих учеников, при этом работа как умственная, так и физическая. Мы говорим о переходе от чисто наглядного способа изучения геометрии к наглядно-лабораторному <…>. Пусть ученики делают все сами, пусть они сделают то, что видели в руках учителя, и что делал он на их глазах. В этом случае рассмотренные на уроке геометрические образы несомненно прочнее запечатлеются в сознании учеников, только тогда с этими образами дети сроднятся и сживутся. И чем чаще они их будут воспроизводить, тем лучше усвоят» [7, с. 11].
Однако развитие научной мысли в этом направлении было приостановлено и даже забыто к середине XX века, когда в методику обучения математики проникли и укрепились идей Н. Бурбаки. Так, начавшаяся в этот период в России Колмогоровская реформа математического образования была основана на принципиально иных идеях - использования в качестве основы построения содержания школьного курса математики абстрактных понятий множества, операций над множествами, формализованного логического языка и абстрактно-дедуктивного метода. Сомнения в корректности понятий, вводимых через интерпретации и содержательные прототипы, в строгости теорем, доказанных экспериментально или с помощью правдоподобных рассуждений, привели в этот период к полному отказу от использования эмпирических методов (в том числе и в преподавании геометрии). Приведем в подтверждение сказанному, слова Столяра А.А. из книги «Логические проблемы преподавания математики» (1965): «Создание формализованного логического языка является важным достижением современной математики… Этим достигнута, в частности, четкость и точность, однозначность смысла логических терминов… Объяснение, даваемое в процессе обучения, в связи с экспериментальным установлением истинности какого-нибудь предложения теории также не относится к языку этой теории» [8, с. 16].
Обоснование образовательной ценности абстрактно-дедуктивного подхода к изложению учебного материала можно найти во многих учебниках методики преподавания математике того периода [9-11]. Ярким примером реализации абстрактно-дедуктивного подхода являются учебные пособия для 9 и 10 классов средней школы авторов В.М. Клопский, З.А. Скопец и др. [12].
Несмотря на критику идей Колмогорова [13] и на контрреформу, последовавшую за ней, идея дедуктивного изложения школьного курса геометрии сохранилась на долгое время в содержании школьных курсов геометрии [14] и практике преподавания.
Постепенно в практике преподавания геометрии стало накапливаться понимание того, что полный отказ от использования эмпирических методов в школьном геометрическом познании приводит к формализму знаний учащихся, к неоправданным сложностям понимания математических абстракций.
В настоящее время отношение к эмпирическим методам в учебном, да и научном математическом познании не является столь радикальным. Эксперимент, опыт, наблюдение признаны полноправными методами учебного познания в работах методистов Епишевой О.Б., Метельского Н.В., Гусева В.А., Мишина В.И. и др. [15-18].
Начиная с 90-х гг. XX века года на страницах специализированных журналов, посвященных вопросам математического образования, стали вновь активно обсуждаться вопросы о возможности организации лабораторных работ по геометрии и других эмпирических методах [19; 20].
В связи с привлечением компьютеров для проведения лабораторных работ в работах по методике обучения математике все чаще стал использоваться термин компьютерный эксперимент (Дубровский В.Н., Середа А.В., Храповицкий И.С., Шуман Г., Иванов С.Г. и др.) [21-25]. Представленные в этих работах описания и примеры использования показывают, что под компьютерным экспериментом авторы понимают манипулирование виртуальными моделями геометрических объектов, сопровождающееся либо сбором данных об изучаемых свойствах этих объектов с фиксацией их в электронной таблице, либо наблюдение за характером изменения этих свойств на экране компьютера.
Сегодня место компьютерного эксперимента в системе методов обучения геометрии только начинает осмысливаться как отдельными учителями – новаторами (Дубровский В.Н, Иванов С.Г., Храповицкий И.С. и др.), так и целыми коллективами ученых разных стран (российско-американский проект Geometry Expressions, проводимый под патронажем американской компьютерной компании, от России в нем участвует Рыжик В.И, заслуженный учитель РФ, к.п.н., соавтор более чем 20 учебников по геометрии; российско-болгарский проект «Методика и информационные технологии в образовании», которым руководят от российской стороны проф. Сергеева Т.Ф. (АСОУ), от болгарской - Гроздев Савва (БАН)).
Самым неоднозначным для всех этих исследователей является вопрос о месте компьютерного эксперимента в системе методов работы с теоремой. Приведем в качестве подтверждения слова В.И. Рыжика:
«Коль скоро математику можно считать наукой экспериментальной или использующей компьютерное экспериментирование, коль скоро при изучении математики экспериментирование как таковое приветствуется, вполне естественно внедрять его в арсенал дидактических средств. Компьютер многократно увеличивает возможности и роль математического эксперимента.
Ответ на вопрос о степени доказанности зависит также от поставленной цели. Если нам нужен некий факт, а откуда он взялся, нам «без разницы» – тогда примем этот факт от компьютера и начнём решать последующие задачи, его используя. А если не хватает уверенности в достоверности полученных результатов, то придётся искать логическое обоснование.
Использование компьютерных доказательств и соответственное подключение рациональных рассуждений делает преподавание более «мягким», если можно так выразиться, более гуманитарным. Всячески подчёркивая логическую составляющую в курсе геометрии, мы должны все время помнить, что логика изложения систематического курса мало похожа на то, как на самом деле добываются знания, какова при этом роль геометрического воображения, прагматической и интеллектуальной интуиции» [26].
Осторожность, с которой специалисты в области теории и методики обучения математике относятся к решению данной проблемы, связана с тем, что в математической науке отношение к компьютерным экспериментам и логическим доказательствам, а также их соотношению, пока не однозначно. Приведем также в подтверждение сказанному слова из выступления Н.А. Вавилова, д.ф.-м.н., профессора кафедры алгебры и теории чисел математико-механического факультета СПбГУ на совместном заседании Санкт-Петербургского Математического общества и секции математики Дома учёных, 23.03.2010: «…В последнее время все чаще обсуждается вопрос об изменении статуса доказательства и уменьшении нашей уверенности в справедливости результатов. Критика и скептицизм подобного рода наиболее энергично, часто и агрессивно озвучиваются в двух следующих направлениях: сомнения в надежности доказательств, выполненных с помощью компьютера; сомнения в надежности исключительно длинных и сложных доказательств ... что касается компьютерных вычислений, то лично я склонен доверять им больше, чем любым математическим доказательствам, кроме самых простых…» [27].
Эта цитата показывает, что ученые-математики и вслед за ними математики-методисты разделились на два лагеря. Одни считают целесообразным ограничиться применением данного метода лишь на этапе выдвижения гипотезы (позиция большинства). Другие [26] – допускают его использование и для обоснования истинности факта теоремы в условиях, когда природа этого факта по каким-то причинам не значима для учащегося или недоступна его пониманию. Есть, конечно, и компромиссная точка зрения [28], которая пока не нашла достойного воплощения из-за принципиальных различий логических и компьютерных доказательств. Она сводится к следующему - компьютерный эксперимент должен стать визуальной основой для проведения логических рассуждений при доказательстве теоремы.
Несмотря на то что именно компромиссный вариант наиболее часто и принимается всеми за правильный, мы считаем, что компьютерный эксперимент целесообразно использовать в комплексе всех трех обозначенных функций.
При этом в зависимости от содержания изучаемой теоремы и места в структуре учебного познания могут быть использованы компьютерные эксперименты разных типов. Так, для открытия теорем – свойств о метрических соотношениях величин целесообразно применение численных компьютерных экспериментов с записью данных в электронную таблицу.
Пример 1. Рассмотрим возможности использования ИГС на отдельных этапах работы с теоремой на примере утверждения: «Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия» (8 класс). Наиболее типичной ошибкой при изучении соотношении величин подобных треугольников для учащихся является проведение ложной аналогии «Если отношение соответственных сторон равно коэффициенту подобия, то это верно и для отношения площадей». Это заблуждение является настолько устойчивым, что единичный контрпример не позволяет убедить учащихся в необходимости отказаться от этой аналогии. В связи с этим работа с утверждением теоремы должна начинаться с накопления и обобщения фактов, альтернативных первичной гипотезе. Для накопления фактов можно использовать возможности ИГС, связанные с построением параметрически заданного динамического чертежа, а также использования функции записи данных в таблицу (рис. 1).
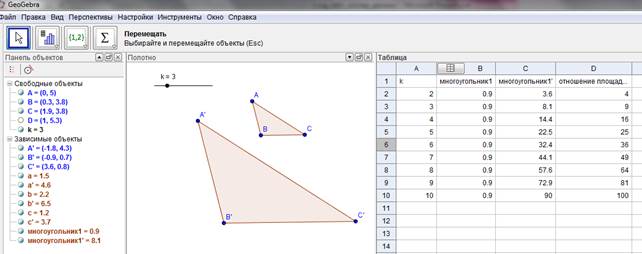
Рисунок 1.
Для открытия теорем – признаков геометрических объектов – конструктивные эксперименты с выводом протоколов построения. Примером может послужить рисунок 2, протокол построения на рисунке 2'.
Пример 2. Докажите, что если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.
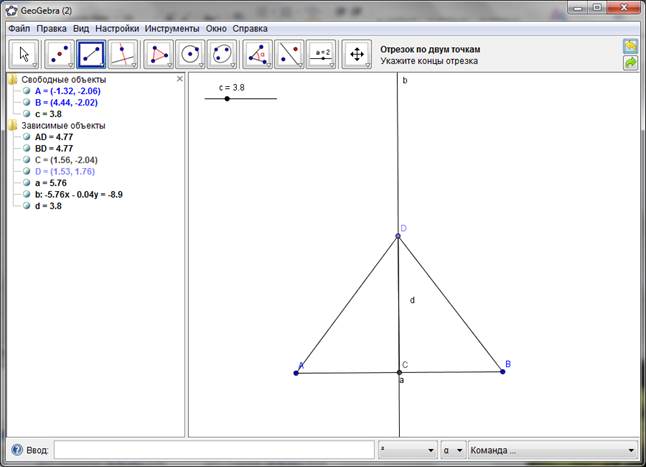
Рисунок 2.
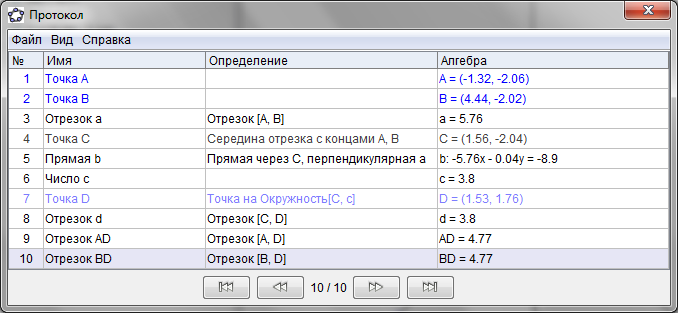
Рисунок 2'.
Для обоснования инвариантности, т.е. динамической устойчивости на параметрах вида и свойств геометрической фигуры, необходимо проведение непрерывного эксперимента со строго определенной динамикой изменения значений параметров.
Пример 3. Данные рассмотренного выше в примере 1 компьютерного эксперимента позволяют учащимся выдвинуть гипотезу о возможном равенстве отношения площадей квадрату коэффициента подобия с объяснением возможных несоответствий некоторых данных накоплением погрешности и заменой точных значений приближенными.
Проверка выдвинутой гипотезы может быть проведена сначала «методом компьютерного доказательства», т.е. установления факта динамической устойчивости отношения площадей подобных треугольников при фиксированном значении коэффициента подобия. Здесь ИГС используется для проведения компьютерного эксперимента, устанавливающего факт независимости отношения площадей подобных треугольников от параметров, задающих исходный треугольник (рис. 3).
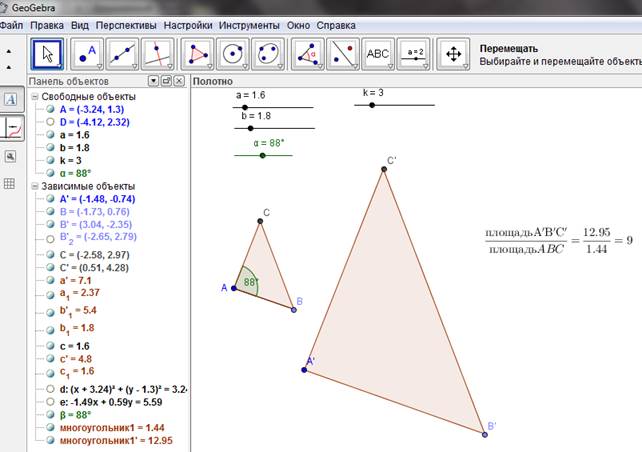
Рисунок 3.
Для сопровождения логического доказательства целесообразно использовать компьютерную визуализацию логических действий.
Пример 4. Доказать равновеликость прямоугольника и параллелограмма с тем же основанием и высотой, т.е. ![]() .
.
Поскольку доказательство равновеликости сводится к преобразованию параллелограмма в прямоугольник путем разбиения его на части и применения к ним параллельного переноса, то ход рассуждений может быть сопровожден преобразованиями динамического чертежа в ИГС
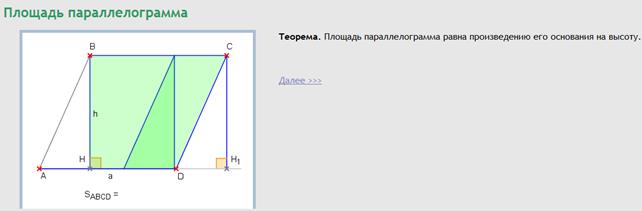
Рисунок 4.
Применение компьютерных экспериментов при изучении геометрии позволяет активизировать познавательную деятельность учащихся, реализовывая на уроке идеи исследовательского обучения [29]. Простота исследований, проводимых методом компьютерного эксперимента, позволяет создавать ситуацию успеха для тех учащихся, кто не слишком искушен в математических выкладках, при этом повышается их учебная мотивация, формируется уверенность в собственных силах и в целом изменяется отношение к математике.
Рецензенты:
Митрохина С.В., доктор педагогических наук, профессор кафедры педагогики, психологии и дисциплин начального образования, Тульский государственный педагогический университет им. Л.Н. Толстого, г. Тула.
Щербатых С.В., доктор педагогических наук, доцент, заведующий кафедрой автоматизированных систем управления и математического обеспечения, Елецкий государственный университет им. И.А. Бунина, г. Елец.
Библиографическая ссылка
Шабанова М.В., Ширикова Т.С. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ В СИСТЕМЕ МЕТОДОВ РАБОТЫ С ТЕОРЕМОЙ // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=9005 (дата обращения: 25.04.2024).



