Актуальность темы: Повсеместный переход к цифровым управляющим системам, замена регуляторов с аналоговым принципом действия на микропроцессорные ставит перед специалистами две задачи. Первая состоит в замене непрерывного закона управления его цифровой реализацией. Вторая - в стремлении усовершенствовать классические законы управления благодаря новым возможностям, предоставляемым цифровой техникой. Направления совершенствования состоят в целенаправленном введении в классические законы нелинейностей, придающих алгоритмам новые полезные свойства.
Цель работы: повышение эффективности проектирования алгоритмического обеспечения цифровых регуляторов для динамических объектов с непрерывным характером производства.
Объект управления: Тестирование различных законов управления проводилось на модели объекта, представляющей собой последовательное соединение звена транспортного запаздывания и апериодического звена второго порядка. Техническим прототипом объекта является нагревательная установка, описанная в [2].
Сравниваемые законы управления: пропорционально-интегральный (ПИ), нелинейный статический, нелинейный динамический, нелинейный релейный.
ПИ-регулятор является самым распространенным общепромышленным регулятором. Однако для многих систем управления, особенно для систем с запаздыванием, ПИ-алгоритм не обеспечивает приемлемых значений показателей качества управления. Возможна коррекция свойств регулятора за счёт целенаправленного введения нелинейности [1]. В нелинейных законах управления сочетается высокое быстродействие с низким или вообще отсутствующим перерегулированием.
Нелинейный релейный закон управления:
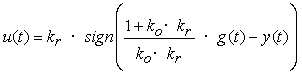 (1)
(1)
где u(t) - управляющее воздействие; kr - настроечный параметр релейного регулятора; ko - коэффициент усиления объекта; g(t) - задающее воздействие; y(t) - выход объекта.
Сомножитель 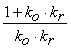 введен для компенсации статической ошибки воспроизведения задания. Нелинейность введена функцией sign(...):
введен для компенсации статической ошибки воспроизведения задания. Нелинейность введена функцией sign(...):
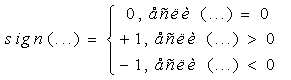 (2)
(2)
Нелинейный статический закон управления:
![]() (3)
(3)
где kp и kn - настроечные параметры регулятора. С помощью параметра kn регулируется степень участия нелинейности в законе управления.
Нелинейный динамический закон управления:
![]() (4)
(4)
где kp, ki, kn1 и kn2 - настроечные параметры регулятора. Параметры kn1 и kn2 позволяют регулировать степень участия нелинейных добавок в пропорциональной и интегральной составляющих ПИ-регулятора соответственно.
Показатели, использованные для оценки качества управления: время переходного процесса, перерегулирование, относительная статическая ошибка, среднеквадратическая ошибка, средняя абсолютная ошибка.
Методика выбора закона управления цифрового регулятора. Она состоит в сопоставлении показателей качества управления объектом при использовании различных законов управления. Для исключения неоднозначности во всех законах управления параметры настройки алгоритмов выбирались в процессе решения задачи параметрической оптимизации так, чтобы обеспечить наилучшее значение показателя качества, выбранного критерием. Поскольку аналитическая форма зависимости показателей качества от параметров алгоритма почти всегда неизвестна, оптимизацию параметров нужно проводить поисковыми методами. В данной работе использован поисковый метод Хука-Дживса [3].
Позиции методики:
Выбрать показатель качества, который для рассматриваемой системы исследователь считает наиболее важным.
Определить параметры модели объекта.
Настроить параметры алгоритмов управления на достижение наилучших значений показателя качества (критерия) при помощи поискового алгоритма Хука-Дживса.
Достигнутые значения критерия являются базой для сравнения оценки эффективности различных законов управления.
Схема вычислительного эксперимента по сопоставлению показателей качества управления, достижимых при использовании различных вариантов алгоритмического обеспечения цифровых регуляторов, приведена на рис. 1.
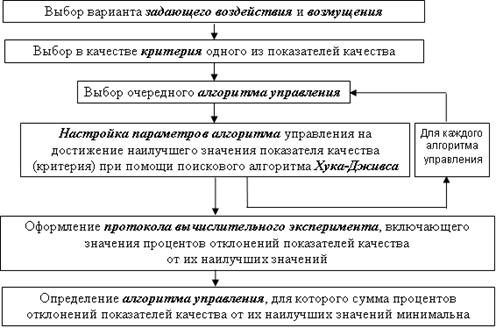
Рис. 1. Методика выбора закона управления
Кроме оптимизируемого критерия необходимо рассчитывать значения других показателей качества, чтобы затем сделать вывод, какой критерий является компромиссным, т.е. при выборе какого показателя качества остальные показатели качества наименьшим образом отклоняются от своих оптимальных значений. Для интерпретации результатов вычислительного эксперимента следует выразить показатели качества в форме отклонений (например, в процентах) от их потенциально наилучших значений.
Для показателей качества «время переходного процесса», «среднеквадрати-ческое отклонение» и «среднее абсолютное отклонение» величина отклонения показателя качества от его наилучшего значения Iij вычисляется по формуле:
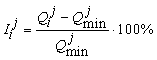 (5)
(5)
где i = 1, ..., 4 - номер закона управления (i = 1 - линейный ПИ-закон управления, i = 2 - нелинейный релейный закон управления, i = 3 - нелинейный статический закон управления, i = 4 - нелинейный динамический закон управления); j = 1, 3, 4 - номер показателя качества (j = 1 - время переходного процесса, j = 3 - среднеквадратическое отклонение, j = 4 - среднее абсолютное отклонение); Qij - значение j-го показателя качества при использовании i-го закона управления; Q jmin - наилучшее значение j-го показателя качества (из достигнутых при использовании различных законов управления).
Для перерегулирования формула (5) неприменима, т.к. его наилучшее значение может оказаться равным нулю, и в этом случае возникнет ошибка деления на нуль. Поэтому для перерегулирования за нулевую отметку принимается 100%, и величина отклонения перерегулирования от его наилучшего значения Ii2 вычисляется по формуле:
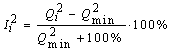 (6)
(6)
Наилучшее значение относительной статической ошибки может оказаться очень маленьким, при этом величина отклонения даже не очень большой статической ошибки от ее наилучшего значения будет большой. А это внесет значительный вклад в сумму процентов отклонений по всем показателям качества (см. таблицу 1). Поэтому для относительной статической ошибки формула (5) неприменима. Вместо нее используется формула расчета отклонения относительной статической ошибки не от наилучшего значения, а от величины «трубки статики», обычно принимаемой равной 5%:
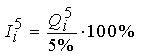 (7)
(7)
Таблица 1. Форма протокола результатов эксперимента
|
Показатель качества \ Закон управления |
Время переходного процесса |
Перерегули- рование |
Средне-квадратическое отклонение |
Среднее абсолютное отклонение |
Относительная статическая ошибка |
Сумма процентов отклонений |
|
ПИ |
I11 |
I12 |
I13 |
I14 |
I15 |
|
|
Релейный |
I21 |
I22 |
I23 |
I24 |
I25 |
|
|
Статический |
I31 |
I32 |
I33 |
I34 |
I35 |
|
|
Динамический |
I41 |
I42 |
I43 |
I44 |
I45 |
|
Анализ таблицы 1 позволяет:
Дать аргументированный ответ на вопрос, не слишком ли велики потери в значениях остальных критериев, если оптимизировать данный (например, рекомендуемый в качестве важнейшего).
Оценить, какой из критериев наиболее близок к компромиссному, т.е. такому, при котором потери в остальных критериях меньше, чем потери при выборе другого критерия (менее компромиссного).
Программный комплекс для выбора законов управления и настройки параметров цифровых регуляторов. В среде MS Visual Studio .NET на языке Visual C++ были разработаны средства компьютерного сопровождения методики выбора закона управления цифрового регулятора. Данный программный комплекс позволяет выполнять следующие функции:
1. Задание параметров объекта и общих параметров моделирования, выбор вида задающего воздействия (постоян-ного, меандрового, синусоидального или случайного коррелированного), возмущающего воздействия (постоянного или случайного коррелированного) и задание их параметров.
2. Применение одного из законов управления:
- 1) выбор закона управления и задание его параметров;
- 2) расчет значений выхода объекта, задающего и управляющего воздействий на каждом такте дискретного времени; построение соответствующих графиков;
- 3) расчет значений показателей качества.
3. Выбор оптимального закона управления:
- 1) выбор критерия оптимизации;
- 2) задание начальных значений параметров регуляторов;
- 3) нахождение оптимальных значений параметров регуляторов;
- 4) для каждого регулятора: расчет значений выхода объекта, задающего и управляющего воздействий на каждом такте дискретного времени; построение соответствующих графиков;
- 5) для каждого регулятора: расчет показателей качества, а также их отклонений от оптимальных значений;
- 6) выбор оптимального закона управления по методике, схема которой приведена на рис. 1.
Предложенная методика и средства ее сопровождения могут быть использованы разработчиками алгоритмического обеспечения цифровых регуляторов для систем локальной автоматизации объектов с непрерывным характером производственного процесса.
Для этого разработчик должен:
Представить модель объекта в форме уравнений в состояниях и определить параметры модели.
Выбрать значение интервала дискретизации непрерывного времени для получения модели объекта в цифровой форме.
Согласно цели системы управления (стабилизация, воспроизведение детерминированной программы, слежение за недетерминированным задающим воздействием) выбрать задающее воздействие из числа представленных в компьютерном сопровождении.
Определить, какая из моделей возмущающих воздействий, представленных в компьютерном сопровождении методики, более всего отвечает особенностям объекта; задать параметры модели возмущающего воздействия.
Провести серию вычислительных экспериментов согласно рис. 1. Перед началом каждого эксперимента выбрать стартовые значения параметров алгоритма управления (вручную).
Сопоставить значения показателей качества, определенных в результате серии вычислительных экспериментов, и обосновать выбор конкретного алгоритма.
Заключение. Основные результаты: разработана методика выбора закона управления цифрового регулятора и программное обеспечение для применения данной методики.
СПИСОК ЛИТЕРАТУРЫ:
- 1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - M.: Наука, 2002. - 752 с.
- 2. Крушель Е.Г., Печеник Н.А. Компьютерная поддержка изучения принципов разработки системы управления объектами с непрерывным характером производства // Известия ВолгГТУ. Серия: Актуальные проблемы управления, вычислительной техники и информатики в технических системах. 2007. №1. С. 81.
- 3. Химмельблау Д. Прикладное нелинейное программирование. - М.: Мир, 1975. - 534 с.
Библиографическая ссылка
Крушель Е.Г., Панфилов А.Э., Панфилова Н.А. МЕТОДИКА И ПРОГРАММНЫЙ КОМПЛЕКС ДЛЯ ВЫБОРА ЗАКОНОВ УПРАВЛЕНИЯ И НАСТРОЙКИ ПАРАМЕТРОВ ЦИФРОВЫХ РЕГУЛЯТОРОВ // Современные проблемы науки и образования. – 2009. – № 5. ;URL: https://science-education.ru/ru/article/view?id=1237 (дата обращения: 20.04.2024).



