Развитие концепции профессионально ориентированного или профессионально направленного обучения студентов педагогических специальностей имеет давнюю историю от формулирования основных принципов профессионально ориентированного обучения студентов педвузов [5] и создания образовательных технологий их реализации [7] до исследования условий и возможностей реализации этого обучения в рамках созданной и внедряемой (ФГОС 3-го поколения) компетентностной парадигмы образования.
Под профессионально направленным обучением математике [2; 6] понимают такое содержание учебного материала и такую организацию его усвоения, которые не нарушают системной логики построения курса математики и позволяют моделировать познавательные и практические задачи профессиональной деятельности специалиста, в нашем случае учителя математики.
Организация профессионально направленного обучения математике предполагает решение следующих задач: определение целей и содержания обучения, отбор средств организации и усвоения этого содержания, повышение мотивации изучения математики. Одним из способов решения этих задач является обогащение содержания дисциплины профессионально ориентированным материалом, то есть материалом, касающимся объектов будущей профессиональной деятельности специалиста, при условии сохранения логической целостности изучаемой дисциплины [5; 6]. Этот способ может быть реализован с помощью профессионально ориентированных задач, которые моделируют элементы профессиональной деятельности специалиста [6].
В профессиональной подготовке учителей математики традиционно используются методические задачи, которые моделируют типичные ситуации профессиональной деятельности педагога. В частности, методические задачи применяются как средство обучения математике будущих и работающих по специальности учителей математики, позволяя формировать и развивать как математические, так и методические знания, умения и навыки [3]. В категориях компетентностного подхода в образовании, и в частности профессионально направленного обучения, методические задачи в обучении по сути выполняют функции профессионально ориентированных задач, поскольку они моделируют элементы профессиональной деятельности специалиста и позволяют развивать профессионально значимые компетенции специалиста в области образования [4], то есть методические задачи, которые применяются в обучении математике будущих и работающих по специальности учителей математики, можно считать частным случаем профессионально ориентированных задач для студентов педагогических специальностей. Однако эти понятия не тождественны: множество методических задач как средства формирования профессионально значимых компетенций студентов педагогических специальностей уже, чем множество профессионально ориентированные задачи для студентов этих специальностей.
Целью нашего исследования является создание системы профессионально ориентированных задач по курсу «Математическая логика».
Опишем и охарактеризуем один из видов профессионально ориентированных задач, которые разрабатывались для студентов, обучающихся по направлению подготовки «Педагогическое образование», профиль «математика», которые не являются методическими, с пояснением целей использования таких задач как профессионально ориентированных и, в данной связи, методических рекомендаций по работе с ними. Опишем возможности работы с такими задачами со студентами и учителями и результаты анализа этой работы. Также опишем опыт работы над такими задачами со школьниками, поскольку он полезен тем, что методической частью работы с такими задачами со студентами и учителями является проектирование работы со школьниками. Такие задачи можно назвать профессионально ориентированными, поскольку они являются средством реализации профессионально направленного обучения, так как связывают вузовскую и школьную математику [5], а также позволяют провести дальнейшую методическую работу с ними.
Этот вид профессионально ориентированных задач в вузовском курсе математики в школьной математике принято называть сюжетными логическими задачами. Они встречаются в курсе математики средней школы, в олимпиадных работах, в конкурсных работах. В курсе математической логики для специальности «педагогическое образование» применяются для обеспечения в изучении этого курса дидактического принципа «от известного к неизвестному», для обеспечения связи между школьным и вузовским курсами математики. А также для осуществления в процессе выяснения теоретической основы решения таких задач, мотивации изучения содержания математических логических операций, для проведения дальнейшей методической работы с такими задачами, заключающейся в выявлении и обсуждении всех способов решения, нахождения способов решения, доступных школьникам, проектировании работы над такими задачами со школьниками.
Пример задачи
Если лягушонок зеленый, то он веселый. Если лягушонок не веселый, то он сидит на берегу. Все лягушата либо зеленые, либо пестренькие. Если лягушонок пестренький, то он плавает в воде (задача взята из варианта математического конкурса «Кенгуру»).
Тогда обязательно
а) все лягушата – пестренькие;
б) все лягушата – веселые;
в) все веселые лягушата – зеленые;
г) все лягушата плавают в воде;
д) все лягушата – не веселые.
Изложим способы решения этой задачи, которые демонстрировались школьниками на занятиях физико-математической школы при КГУ им. К.Э. Циолковского (2002-2015 гг.), студентами КГУ им. К.Э. Циолковского на занятиях по математической логике (2002-2015 гг.), учителями средних общеобразовательных школ г. Калуги и Калужской области на курсах повышения квалификации учителей математики (2014-2015 гг.). В каждой группе (2013-2014, 2014-2015 учеб. гг., 200 человек) до изучения соответствующего материала проводилась письменная самостоятельная работа по решению сюжетных логических задач. Результатом анализа и обобщения продуктов этих самостоятельных работ являются изложенные ниже способы решения, выявленные типичные ошибки, приведенные ниже замечания и выводы.
Способ 1. Применяется схематическое изображение множеств и логических связей между элементами этих множеств.
Одно и то же множество лягушат изобразим тремя кругами.
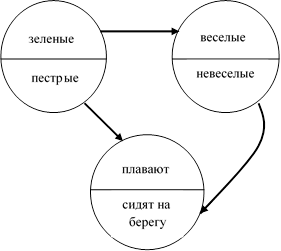
Рис. 1. Иллюстрация к задаче.
Каждый круг поделим на две части для дополняющих друг друга свойств лягушат: зеленый/пестренький, веселый/невеселый, плавает в воде/сидит на берегу. Логические связи между элементами множеств изобразим стрелками.
Из условий «Если лягушонок зеленый, то он веселый», «Если лягушонок пестренький, то он плавает в воде» и «Все лягушата либо зеленые, либо пестрые» делаем вывод, что «Все лягушата либо веселые, либо плавают». Так как «Если лягушонок не веселый, то он сидит на берегу», то есть «Все невеселые лягушата сидят на берегу», значит, «Плавающих невеселых лягушат нет», то есть «Плавают только веселые лягушата». Таким образом, получаем, что все лягушата - веселые.
Способ 2. Применяется схематическое изображение множеств с помощью кругов Эйлера.
Данный способ отличается от предыдущего только иллюстрацией условий задачи, рассуждения же аналогичны предыдущему способу.
Способ 3. схематическое изображение множеств с помощью отрезков.
Изображаем три одинаковых отрезка, располагая их строго один под одним.
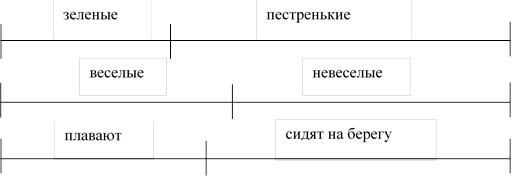
Рис. 2. Иллюстрация к задаче.
Каждый отрезок отображает одно и то же множество лягушат. На первом отрезке изображаем свойство: зеленый или пестренький. На втором отрезке – веселый или невеселый. На третьем отрезке – сидит на берегу или плавает в воде. Логические связи между элементами множеств на схеме отображаем так. Например, для условия «Если лягушонок зеленый, то он веселый» отрезок, соответствующий зеленым лягушатам, попадает внутрь отрезка, соответствующего веселым лягушатам, при совмещении этих отрезков.
Таким образом, на схеме отображены логические связи «Если лягушонок зеленый, то он веселый», «Если лягушонок невеселый, то он сидит на берегу». Условие «Если лягушонок пестренький, то он плавает в воде» при этом выполнить на схеме не удается, поэтому сформулируем равносильное ему условие и доработаем схему. Условие «Если лягушонок пестренький, то он плавает в воде» сформулируем другими словами: «Все пестрые лягушата плавают в воде». Это значит, что «Нет пестрых лягушат, которые сидят на берегу», то есть «На берегу сидят только зеленые лягушата». Поэтому на схеме «отрезаем» пестрых лягушат, которые сидят на берегу, поскольку таких лягушат нет, и дорисовываем зеленых лягушат, которые сидят на берегу. При этом дорисовываемые лягушата веселые, так как по условию «Если лягушонок зеленый, то он веселый». Таким образом, остаются только веселые лягушата.
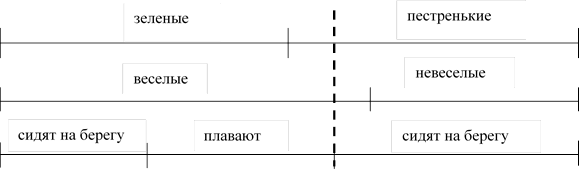
Рис. 3. Иллюстрация к задаче.
Способ 4. Решение с помощью таблиц.
Исходная таблица – таблица 1. Таблица имеет 8 ячеек (пронумерованы от 1 до 8). Например, ячейке 3 соответствует зеленый, веселый лягушонок, который сидит на берегу.
Таблица 1
|
|
Плавает |
Сидит на берегу |
||
|
Зеленый
|
веселый -1- |
невеселый -2- |
веселый -3- |
невеселый -4- |
|
Пестрый
|
веселый -5- |
невеселый -6- |
веселый -7- |
невеселый -8- |
Условие «Если лягушонок зеленый, то он веселый» выполняется в таблице 2. Неподходящие случаи вычеркиваются.
Таблица 2
Предыдущее условие и условие «Если лягушонок не веселый, то он сидит на берегу» выполняются в таблице 3.
Таблица 3
Два предыдущих условия и условие «Если лягушонок пестренький, то он плавает в воде» выполняются в таблице 4.
Таблица 4
Таким образом, остались только веселые лягушата.
Изложенные выше решения представляют собой некоторое упорядочение решений, которые предлагались школьниками, студентами, учителями, по содержанию рассуждений, а также некоторое обобщение по способу краткой записи (схемы, таблицы), которая помогает решать такие задачи.
Также анализируя работы школьников, студентов, учителей, можно сделать следующие замечания и выводы.
1. Понимание логической операции «конъюнкция» 
(выражается словами «Элемент обладает свойствами А и Б») в решении этих задач демонстрируется с точки зрения математической логики.
Логическая операция «следования» 
(выражается словами «Если элемент обладает свойством А, то он обладает свойством Б»), как правило, понимается как в математической логике, тем не менее допускаются ошибки. Например, такие:
- считают, что имеет место только один случай «Элемент обладает свойствами А и Б»,
- считают, что утверждению «Если элемент обладает свойством А, то он обладает свойством Б» равносильно или является его следствием утверждение «Если элемент не обладает свойством А, то он не обладает свойством Б».
Логическая операция «дизъюнкция» 
(выражается словами «Элемент обладает либо свойством А, либо свойством Б») в таких задачах нередко трактуется выполнением только двух случаев: либо элемент обладает свойством А и не обладает свойством Б, либо элемент не обладает свойством А и обладает свойством Б. Случай, когда элемент обладает и свойством А, и свойством Б, опускается.
2. Используется справедливая замена предложения «Если элемент обладает свойством А, то он обладает свойством Б»
· ему эквивалентной формулировкой (в смысле используемых в математических текстах формулировок для логической операции следования ): «Все элементы со свойством А обладают свойством Б»;
· и ему эквивалентными (в категориях математической логики) предложениями:
- «Нет элементов со свойствами А и 
» (
),
- «Если элемент обладает свойством , то он обладает свойством 
(
).
3. Используется схематическое изображение логической операции следования
· с помощью отрезков: отрезок для элементов со свойством А попадает внутрь отрезка для элементов со свойством Б,
· с помощью кругов Эйлера: круг для элементов со свойством А расположен внутри круга для элементов со свойством Б.
4. Имеет место выделение комбинаций свойств, для которых выполняется то или иное утверждение. Например, утверждение «Если элемент обладает свойством А, то он обладает свойством Б» как математическая логическая операция «следование» выполняется для следующих комбинаций свойств:
- элемент обладает свойствами А и Б,
- элемент не обладает свойством А и обладает свойством Б,
- элемент не обладает свойством А и не обладает свойством Б.
Данный момент прослеживается в способах решения 3 и 4.
5. Нередко допускается логическая ошибка, когда вместо доказательства следствия проверяют, выполняются ли одновременно все условия вместе с заключением. Если выполняются, то делают вывод, что следствие верно. Однако такое рассуждение ошибочно, поскольку при таком рассуждении вместо доказательства тавтологии 
, 
доказывается непротиворечивость формулы 
. Однако из того, что формула непротиворечива, не следует, что тавтология.
6. При обобщении способы 1, 2 и 3 решения сюжетных логических задач правильнее будет назвать способами схематического представления условий сюжетных логических задач, которые вместе с пониманием содержания логических операций, знанием утверждений, равносильных утверждению «Если элемент обладает свойством А, то он обладает свойством Б», скорее являются способами поиска решения задач, чем способами решения задачи, поскольку не гарантируют получение решения каждой следующей задачи данного типа, согласно пониманию содержания понятия «способ решения задачи» в трудах ряда исследователей, анализ подходов к трактовке содержания понятий «задача», «способ решения задачи», представленных в этих трудах, проведен в работе [3].
В отличие от способов 1, 2 и 3 способ 4 является именно способом решения в указанном понимании, но он неудобно представлен. Его доработкой является изложенный ниже 5-й способ. Назовем его способом перебора.
Способ 5. Перебор.
У лягушат есть три свойства: веселый/невеселый, зеленый/пестренький, сидит на берегу/плавает в воде.
Значит, могут быть 8 комбинаций этих свойств:
1) веселый, зеленый, сидит на берегу;
2) веселый, зеленый, плавает в воде;
3) веселый, пестренький, сидит на берегу;
4) веселый, пестренький, плавает в воде;
5) невеселый, зеленый, сидит на берегу;
6) невеселый, зеленый, плавает в воде;
7) невеселый, пестренький, сидит на берегу;
8) невеселый, пестренький, плавает в воде.
Условие «Если лягушонок зеленый, то он веселый» исключает 5) и 6) случаи.
Условие «Если лягушонок не веселый, то он сидит на берегу» исключает 6) и 8) случаи.
Условие «Если лягушонок пестренький, то он плавает в воде» исключает 3) и 7) случаи.
Таким образом, условию удовлетворяют 1), 2) и 4) случаи. В этих случаях лягушонок – веселый. Значит, получаем ответ, что все лягушата веселые.
Приведем некоторые методические рекомендации по работе с сюжетными логическими задачами со школьниками.
Для решения сюжетных логических задач 5-м способом необходимо знать, на каких комбинациях свойств выполняется утверждение «Если элемент обладает свойством А, то он обладает свойством Б», а также утверждения «Элемент обладает свойствами А и Б», «Элемент обладает свойством А или обладает свойством Б» согласно определению логических операций «следование», «конъюнкция», «дизъюнкция» в математической логике, поскольку в сюжетных логических задачах все логические операции понимаются как математические. В данной связи перед решением таких задач или в ходе разбора первой такой задачи следует провести работу, которая нацелена на знакомство с математическими логическими операциями (с их существованием), их содержанием и словесными формулировками для этих операций.
В ходе работы с условием сюжетной логической задачи со школьниками необходимо научить их выделять пары дополняющих свойств, выписывать все возможные комбинации этих свойств, определять их количество. Например, в задаче про лягушат данную работу можно спланировать с помощью следующих опорных вопросов:
- «Какие бывают лягушата? По цвету? По настроению? Что они делают? Значит, у каждого лягушонка 3 свойства. Какими могут быть лягушата?»
Для перечисления всех возможных комбинаций свойств при решении первой такой задачи можно составить дерево разбора. Затем заметить закономерность в заполнении получившегося списка.
В работе со студентами, с учителями такие задачи можно использовать с целью мотивации изучения математической логики и обеспечения дидактического принципа «от известного к неизвестному», поэтому дальнейшая работа сводится к изучению содержания математических логических операций, и построена она может быть следующим образом. Приведем фрагмент лекции по теме «Логические операции» (авторская).
После выяснения способов решения студентами, учителями задачи про лягушат, существенных моментов этих решений, допущенных студентами, учителями ошибок, введем логическую операцию «следование». Для этого разберем предложение «Если лягушонок зеленый, то он веселый». В нем говорится о множестве лягушат, у лягушат есть два свойства: зеленый/не зеленый (пестренький), веселый/невеселый. Значит, обобщить это предложение можно так: «Если элемент некоторого множества обладает свойством А, то он обладает свойством Б». Кратко запишем: . Здесь А обозначает элементы, обладающие свойством А, а Б – элементы, обладающие свойством Б, 
- математическая логическая операция «следование». Назвали ее математической, так как она определена в математической логике и применяется в математике. Как определяется эта операция?
Вариантов владения свойствами А и Б всего 4:
1) элемент обладает свойством А и обладает свойством Б, кратко запишем 
,
2) элемент обладает свойством А и не обладает свойством Б, кратко запишем 
,
3) элемент не обладает свойством А и обладает свойством Б, кратко запишем 
,
4) элемент не обладает свойством А и не обладает свойством Б, кратко запишем 
.
Каждая логическая операция определяется так: указывается, какие из этих четырех вариантов выполняются. Для операции следования выполняются все, кроме 2-го.
Далее решаем задачу про лягушат методом перебора.
После решения задачи следует рассмотреть графическую иллюстрацию операции «следования» с помощью кругов Эйлера, с помощью отрезков и соотнести эти иллюстрации с определением операции.
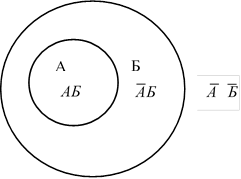
Рис. 4. Графическая иллюстрация операции «следования» с помощью кругов Эйлера.
Графическая иллюстрация логической операции следования .
Далее с помощью этой иллюстрации установить равносильность утверждений (пояснив понятие равносильности утверждений, как выполнение каждого из них на одном и том же наборе комбинаций свойств) «Если элемент обладает свойством А, то он обладает свойством Б», «Все элементы, обладающие свойством А, обладают свойством Б», «Нет элементов, которые обладают свойством А и не обладают свойством Б» и вернуться к анализу способов решения студентами, учителями задачи про лягушат, обсудив с ними теоретическую основу решения таких задач со школьниками.
В продолжение знакомства с языком и символикой математической логики ввести обозначения: утверждение «элемент обладает свойством А» обозначают А=1, утверждение «элемент не обладает свойством А» обозначают А=0; и составить таблицу истинности для логической операции «следование».
После изучения со студентами содержания всех логических операций, упражнений по составлению таблиц истинности для формул логики предложений, доказательства равносильности формул с помощью таблиц истинности, решения сюжетных логических задач через составление формулы логики предложений и ее таблицы истинности, соотнесения этого способа решения с 5-м способом перебора, обсуждения вопроса о возможности адаптации математической задачи и способа ее решения для разных аудиторий приходим к решению профессионально ориентированных задач по составлению сюжетных логических задач. Задачи на составление математических задач для школьников относятся к методическим задачам и в работе [3] выделены в отдельный вид методических задач, используемых при изучении математических курсов со студентами педагогических специальностей. Такие задачи представляют собой еще один вид профессионально ориентированных задач, применяемых в курсе математической логики для студентов педагогических специальностей.
Пример задачи
Для тавтологии 
составьте сюжетную логическую задачу (формула для задачи про лягушат).
Примеры решения
1. Возьмем множество барабашек. Так как в формуле три разные буквы, то у барабашек должно быть три свойства. Пусть свойства следующие:
- 
– пушистый, 
– не пушистый,
- 
– не любит кисель, 
– любит кисель,
- 
– крикливый, 
– не крикливый.
Получаем задачу: если барабашка пушистый, то он не любит кисель. Если барабашка любит кисель, то он крикливый. Если барабашка не пушистый, то он не крикливый. Значит, все барабашки не любят кисель. Верно ли сделан вывод?
2. Возьмем множество котят со следующими свойствами:
- – милый, – не милый,
- – шкодливый, – не шкодливый,
- – играет в прятки, – не играет в прятки.
Получаем задачу: если котенок милый, то он шкодливый. Если котенок не шкодливый, то он играет в прятки. Если котенок не милый, то он не играет в прятки. Значит, все котята шкодливые. Верно ли сделан вывод?
3. Пусть утверждение значит «Таня сердится на Рому», тогда утверждение – «Таня не сердится на Рому». Утверждение – «Рома виноват перед Таней», – «Рома не виноват перед Таней». Утверждение – «Рома должен извиниться», – «Рома не должен извиняться».
Получаем задачу: если Таня сердится на Рому, то Рома виноват перед Таней. Если Рома не виноват перед Таней, то Рома должен извиниться. Если Таня не сердится на Рому, то Рома не должен извиняться. Значит, Рома виноват перед Таней. Верно ли сделан вывод?
Заметим, что к работе по составлению сюжетных логических задач среди студентов бакалавриата, студентов магистратуры и учителей математики больший интерес проявляли студенты магистратуры, которые недавно окончили бакалавриат и на момент обучения в магистратуре работали учителями в школах. Слабый интерес к данной работе учителей на курсах повышения квалификации в таком случае можно объяснить в большинстве своем великовозрастностью аудитории: посещавшие курсы учителя уже давно закончили вуз, забыли курс математической логики и поэтому имели значительные затруднения с оперированием аппаратом математической логики. Студентам бакалавриата эта работа была неинтересна потому, что они не являлись работающими учителями, а некоторые из них, как выяснялось в беседах со студентами, и не планировали работать в школе. К анализу способов решения сюжетных логических задач к изложению 5-го способа решения наибольший интерес проявили именно учителя на курсах повышения квалификации, поскольку содержание материала не требовало дополнительных знаний по математической логике и этот материал они могли использовать в своей работе в школе. Студенты магистратуры и учителя на курсах повышения квалификации отметили 5-й способ решения как наиболее простой и удобный.
Описанные в статье два вида профессионально ориентированных задач позволяют «оживить» изучение математической логики со студентами педагогических специальностей. Если студент в дальнейшем видит себя учителем математики или уже является работающим учителем математики, то решение таких задач повышает интерес к изучению курса математической логики, что решает одну из задач организации профессионально направленного обучения. Также эти задачи предоставляют студентам возможность попрактиковаться как педагогам, получить опыт проектирования и планирования работы со школьниками.
Рецензенты:
Дробышев Ю.А., д.п.н., профессор, профессор кафедры «Высшая математика и статистика» Калужского филиала Финансового университета при Правительстве РФ, г. Калуга;
Щербатых С.В., д.п.н., доцент, проректор по учебной работе, профессор кафедры «Математика и методика ее преподавания» ФГБОУ ВПО «Елецкий государственный университет им. И.А. Бунина», г. Елец.
Библиографическая ссылка
Баданова Т.А., Трунтаева Т.И. ПРОФЕССИОНАЛЬНО ОРИЕНТИРОВАННЫЕ ЗАДАЧИ В КУРСЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ // Современные проблемы науки и образования. – 2015. – № 2-2. ;URL: https://science-education.ru/ru/article/view?id=21679 (дата обращения: 17.04.2024).