Процессы переноса импульса и тепла в пограничном слое
Теоретическое описание процессов теплообмена при турбулентном режиме течения представляет собой, по сравнению с ламинарным режимом, гораздо более сложную задачу. Это связано с незамкнутостью системы уравнений, описывающей такие течения. В настоящее время предложено много полуэмпирических моделей для описания турбулентного течения, которые хорошо согласуются с опытом. Однако эти модели в основном относятся к течениям в гидравлически гладких трубах. Течения в шероховатых трубах обследованы менее полно, особенно в переходной области от течения в гидравлически гладкой трубе к течению с квадратичным сопротивлением [3-5, 9, 10].
Рассмотрим течение однофазного турбулентного потока вдоль твердой поверхности.
Выражения для теплового потока и касательного напряжения (поток импульса) согласно молекулярного и турбулентного переноса имеют известную форму:
![]() , (1)
, (1)
![]() , (2)
, (2)
где y - расстояние от поверхности до рассматриваемой точки, м; ρ - плотность, кг/м3; a, aT - коэффициенты молекулярной и турбулентной температуропроводности, м2/с; ν, νT - коэффициенты молекулярной и турбулентной вязкости, м2/с; Т - температура, °С; u - скорость, м/с; cp - удельная теплоемкость, Дж/(кг·К).
Потоки тепла и импульса на стенке (т.е. при y = 0), также можно записать в виде:
![]() , (3)
, (3)
![]() , (4)
, (4)
где при «∞» - параметры ядра потока, а при «СТ» - на стенке.
В выражении (4) используется коэффициент импульсоотдачи γ (аналог коэффициента теплоотдачи α), который характеризует скорость переноса импульса. Коэффициент γ стал широко применяться в работах Дьяконова [1, 2, 6] и др. для моделирования процессов переноса в одно- и двухфазных средах.
Из (1) - (4) записывают интегралы [1, 11]:
![]() , (5)
, (5)
![]() , (6)
, (6)
Для решения выражений (5) и (6) необходимо знать зависимость коэффициента турбулентного обмена по координате Oy.
Связь между коэффициентом турбулентного обмена и гидродинамическими характеристиками турбулентного течения дается локальной теорией турбулентности.
Потоки тепла и импульса связаны со значениями на поверхности (при y = 0) функциями [11]
![]() , (7)
, (7)
![]() , (8)
, (8)
где F(y) - функция определяющаяся геометрическими условиями.
После того как подставим выражения (7), (8) в (5), (6) и введем коэффициенты теплоотдачи α и импульсоотдачи γ получим:
![]() , (9)
, (9)
![]() , (10)
, (10)
Если значение y0 несоизмеримо мало по сравнению с геометрическими размерами, то можно предполагать F(y)=1 [11].
В результате приходим к следующим выражениям для определения коэффициентов импульсо- и теплоотдачи в пограничном слое толщиной δ:
![]() , (11)
, (11)
![]() , (12)
, (12)
где τ*, q* - безразмерные потоки импульса и тепла.
Выражения (11), (12) являются достаточно общими и позволяют вычислить коэффициенты переноса импульса и тепла на основе коэффициентов молекулярной диффузии, а также известного характера изменения коэффициентов турбулентного обмена νT(y), aT(y) и относительных потоков τ* = τ(y)/ τ0; q* = q(y)/q0. В выражениях (11) и (12) не учитывается конвективный перенос, т.к. известно, что его роль в пограничном слое в направлении оси Oy мала.
Если известны функции турбулентного обмена νT(y), aT(y) выражающие зависимость коэффициента турбулентного переноса от расстояния до поверхности y, то не составит труда вычислить все величины характеризующие процессы переноса.
В литературе известно большое количество различных функций νT(y) для двух- и трехслойных моделей пограничного слоя с учетом затухания турбулентности в вязком подслое.
Гидродинамическая аналогия
Для турбулентного пограничного слоя в случае Pr = 1 и dP/dx = 0 следует подобие безразмерных профилей скорости и температуры и полная аналогия переноса (аналогия Рейнольдса).
При Pr≠1 используется поправка Чилтона-Кольборна:
![]() , (13)
, (13)
где StT = α/(ρcpU∞) - число Стантона; Cf - коэффициент трения; Pr - число Прантля.
Из уравнений (3), (4) и (13) следует связь между коэффициентами переноса импульса γ и тепла α [6]:
![]() . (14)
. (14)
Модели турбулентности в пограничном слое
Развитием теории пристенной турбулентности была форма представления распределения турбулентной вязкости с использованием демпфирующего множителя позволяющего получать гладкую зависимость (кривую) турбулентной вязкости и соответственно скорости [8].
![]() . (15)
. (15)
где u* - динамическая скорость трения, м/с; ![]() - безразмерная координата.
- безразмерная координата.
На основе теории затухании волновых функций Ван-Дристом была получена следующая формула демпфирующего фактора, показанная в общем виде в [8]:
![]() , (16)
, (16)
где n = 2 (в оригинальной работе Ван-Дриста), b = 0,0092 - опытный коэффициент Дайслера.
Демпфирующий множитель KD учитывает скорость затухания турбулентных пульсаций при приближении к стенке.
Представляя верхний предел интегрирования в виде переменной величины в выражении (11), в результате численного интегрирования в данной статье получена зависимость, которая хорошо апроксимируется представленной ниже функцией:
![]() , (17)
, (17)
где 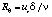 - безразмерная толщина пограничного слоя.
- безразмерная толщина пограничного слоя.
Многие авторы полагают, что изменение турбулентной вязкости в вязком подслое пропорционально у4. На основании этого Дайслер и Ханратти получили формулу:
![]() , (18)
, (18)
где k ≈ 0,01 - коэффициент пропорциональности.
Отсюда представлены следующие функции [8, 12]:
![]() ,
, ![]() <5; (19)
<5; (19)
![]() , 5<
, 5<![]() ≤30; (20)
≤30; (20)
![]() при
при ![]() >30. (21)
>30. (21)
После интегрирования (11) с данными функциями в статье получена зависимость для коэффициента переноса импульса в виде:
![]() , (22)
, (22)
Консервативные свойства пограничного слоя
Полученные в данной работе уравнения (17) и (22) для определения коэффициентов переноса импульса справедливы для плоского пограничного слоя (или с малой кривизной поверхности тел) без возмущений. Ниже рассмотрен подход определения параметров уравнений для коэффициентов γ и α для пограничного слоя с различными возмущениями используя консервативные свойства пограничного слоя (т.е. наличие возмущений можно учесть параметрически).
В результате получена формула для шероховатой пластины [6]:
![]() , (23)
, (23)
где «ш» - параметры для шероховатой поверхности.
Значение толщины δ (или Rδ) для пограничного слоя с возмущениями также можно получить из выражений для γ (17) и (22) и потокового соотношения (4). Соответственно имеем:
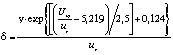 , (24)
, (24)
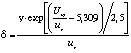 , (25)
, (25)
На основе выражений (17) и (22) и аналогии (14) записаны следующие зависимости для расчета коэффициента теплоотдачи в турбулентном пограничном слое:
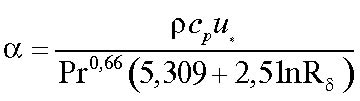 , (26)
, (26)
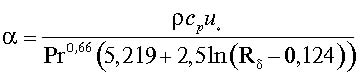 . (27)
. (27)
где динамическую скорость u* можно определить на основе использования перепада давления или коэффициента гидравлического сопротивления ξ.
Расчет теплоотдачи в каналах круглого сечения с элементами интенсификации
Рассмотрим течение вязкой жидкости в трубах с элементами интенсификации, в частности в канале с ленточным завихрителем. В выражениях (26) и (27) динамическую скорость u* запишем через коэффициент сопротивления ξ, используя известные выражения [5, 13]:
![]() ,
, ![]() (28)
(28)
где θ - угол закрутки потока; Re - число Рейнольдса.
Толщину пограничного слоя δ найдем из выражений (24) или (25), что дает близкие результаты.
На рис. 1 представлены результаты расчетов безразмерного комплекса (где Nu - число Нуссельта) и сравнение с опытными данными при закрученном движении потока в трубе. Расхождение результатов составляет около 10-12%.
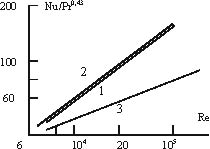
Рис. 1. Зависимость комплекса Nu/Pr0,43 от числа Re в канале с ленточным завихрителем: 1 - расчет по уравнению (26); 2 - экспериментальные данные [5, 13]; 3 - для осевого потока
Аналогичные результаты дает выражение (27).
Расчет теплоотдачи для шероховатой пластины
Рассмотрим применение полученных выше уравнений (26) и (27) для расчета коэффициентов теплоотдачи от поверхностей с элементами интенсификации, например, с шероховатой поверхностью. В работе рассматривалась песочная шероховатость.
Пограничный слой на шероховатой поверхности представляется состоящим из двух областей: внутренней области вблизи стенки, распределение скоростей в которой полностью зависит от местных параметров потока, и внешней области, расположенной дальше от стенки.
Фактически теоретической моделью турбулентного течения около шероховатой поверхности является пограничный слой на гладкой стенке с измененными граничными условиями на ней [7].
Параметры пограничного слоя (u*, δ) на поверхности с элементами интенсификации, отличаются от параметров гладкого пограничного слоя.
Динамическую скорость в пограничном слое на шероховатой поверхности найдем по известному выражению только с коэффициентом трения шероховатой поверхности:
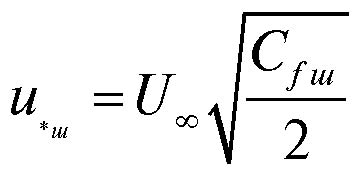 . (28)
. (28)
На рис. 2 представлены результаты расчета по (26) и сравнение с расчетом по теоретическим и эмпирическим зависимостям [3, 6, 12] (Аналогичные результаты получены по уравнению (27)).
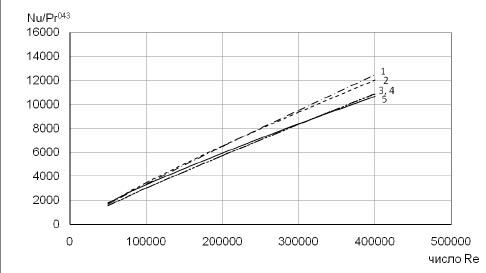
Рис. 2. Зависимость комплекса Nu/Pr 0,43 от числа Re при обтекании шероховатой пластины
1 - расчет по уравнению (26); 2 - данные по [3]; 3 - расчет по уравнению (27);
4 - данные по [6]; 5 - данные по [12]
На основании представленных результатов можно сделать вывод, что уравнения (26), (27) удовлетворительно согласуются с известными выражениями для расчетов коэффициентов теплоотдачи и опытными данными. Расхождение результатов лежит в пределах 10-15%.
Полученные уравнения (26) и (27) с параметрами (23)-(25) являются модификацией гидродинамической аналогии для пограничных слоев с различными видами интенсификации теплообмена и рекомендуются к практическому использованию.
СПИСОК ЛИТЕРАТУРЫ
- Дьяконов С.Г., Елизаров В.И., Лаптев А.Г. Модель массотдачи в барботажном слое на основе концепции активного входного участка // ТОХТ. 1991. Т.25. № 6. С 783-795.
- Дьяконов С.Г., Елизаров В.И., Лаптев А.Г. Теоретические основы и моделирование процессов разделения веществ. Казань: Изд-во Казанск. ун-та. 1993. 437 с.
- Жукаускас А.А. Конвективный перенос в теплообменниках. М.: Наука, 1982. 472 с.
- Кутателадзе С.С. Основы теории теплообмена. Издание 5 переработанное и дополненное.,М.: Атомиздат. 1979. 416.с.
- Кутателадзе С.С. Теплопередача и гидродинамическое сопротивление: Справочное пособие. М.: Энергоатомиздат. 1990. 367с.
- Лаптев А.Г. Модели пограничного слоя и расчет тепломассообменных процессов. Казань: Изд-во Казанск. ун-та. 2007. 500 с.
- Леонтьев А.И., Олимпиев В.В. Влияние интенсификаторов теплообмена на теплогидравлические свойства каналов // Теплофизика высоких температур. 2007. Т. 45. № 6. С. 925-939.
- Лойцянский Л.Г. Механика жидкости и газа. - 7-е изд., испр. М.: Дрофа. 2003. 840с.
- Мигай В.К. Моделирование теплообменного и энергетического оборудования. Ленинград: Энергоатомиздат. 1987. 263 с.
- Петухов Б.С., Генин Л.Г., Ковалев С.А. Теплообмен в ядерных энергетических установках: Учебн.пособие для ВУЗов. Под ред. Б.С. Петухова. М.: Атомиздат. 1974. 407 с.
- Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. - 3-е изд. М.:Наука. 87. 502.с.
- Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974. 712 с.
- Щукин В.К. Теплообмен и гидродинамика внутренних потоков в полях массовых сил. М.: Машиностроение. 1980. 240 с.
Библиографическая ссылка
Лаптев А.Г., Бажиров Т.С., Ахметов Р.Н. МОДИФИКАЦИЯ ГИДРОДИНАМИЧЕСКОЙ АНАЛОГИИ ДЛЯ ИНТЕНСИФИЦИРОВАННОГО ТЕПЛООБМЕНА // Современные проблемы науки и образования. – 2010. – № 4. ;URL: https://science-education.ru/ru/article/view?id=4513 (дата обращения: 20.04.2024).



