Увеличение длины периметра охраняемой зоны при использовании радиолокационной технической системы охраны (РЛТСО) приводит к возрастанию затрат, связанных с идентификацией вида нарушителя (Н). Использование аппаратуры, определяющей некоторые параметры Н, например, часть его геометрических размеров, позволит обеспечить распознание типа Н и как следствие - снизить количество ложных тревог из-за объектов, не представляющих угрозы для охраняемой зоны.
Целью работы является разработка алгоритма восстановления вида функции пропускания 
одномерного непрозрачного для электромагнитного поля (ЭМ-поля) Н по дифракционной картине для определения части его геометрических размеров и сравнение его с преобразованием Френеля.
1. Восстановление вида одномерной функции пропускания нарушителя по его дифракционной картине
На рисунке 1 приведена схема пересечения охраняемой зоны РЛТСО [1] нарушителем, моделируемым в виде эллиптического цилиндра [2]. Нарушитель перемещается в охраняемой зоне параллельно оси X, при этом координаты его центра и размеры по осям X, Y и Z равны соответственно x0, y0, RН и 2a, 2b и 2c. Векторы 
и 
проведены из точек P0 и P расположения передатчика (ПРД) и приемника (ПРМ) РЛТСО в произвольную точку поверхности Q нарушителя, через которую проходит и вектор нормали 
.
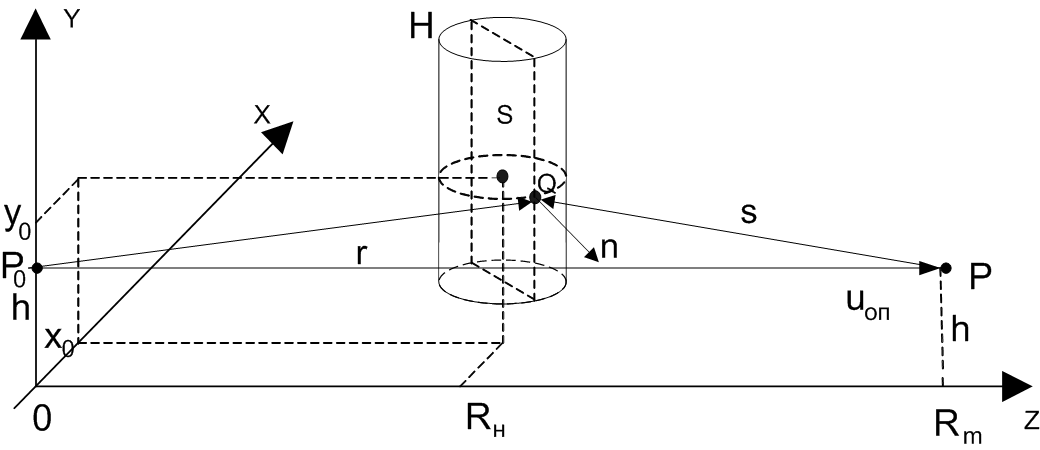
Рисунок 1. Схема пересечения нарушителем охраняемой зоны РЛТСО. Н - модель нарушителя, и - векторы, проведенные из точек P0 и P расположения ПРД и ПРМ РЛТСО в точку Q поверхности нарушителя, - вектор нормали к поверхности
Для определения геометрических размеров Н используем зависимость комплексной амплитуды ЭМ-поля 
в точке P от изменяющейся при пересечении Н охраняемой зоны РЛТСО координаты x0. При определении воспользуемся дифракционной формулой Френеля - Кирхгофа [3]:
, (1)
где r,s - модули векторов 
и , 
, λ - длина волны ЭМ-поля, S - поверхность, по которой осуществляется интегрирование, dS - элемент площади этой поверхности.
Разложение в выражении (1) r и s в ряд в окрестности x0, y0 с последующим отбрасыванием членов, начиная с квадратичного, приводит к дифракции Фраунгофера, а начиная с кубического - к дифракции Френеля [4]. Для этих типов дифракции восстановление функции пропускания возможно при использовании обратных преобразований Фурье и Френеля соответственно. Наряду с этим обратные преобразования Фурье и Френеля являются упрощениями некоторого более общего преобразования, также как дифракционные интегралы Фраунгофера и Френеля являются частными случаями выражения (1). Для определения его одномерного вида используем случай дифракции ЭМ- волн на щели в плоском экране с шириной 2а по оси x от протяженного источника, явлющегося предельным случаем для соотношения размеров нарушителя 
и 
. Для него выражение (1) преобразуется к виду:
, (2)
где 
, 
.
Представляя в (2) выражения 
и 
в виде разложения в ряд по степеням 
получим: 
и 
Последние представления возможны только при выполнении условий типа
, 
.(3)
Подставляя полученные упрощенные выражения для r(x0) и s(x0) в показатель экспоненты выражения (2) и считая их равными соответственно 
и 
в знаменателе подынтегральной функции, придем к следующему упрощенному виду зависимости комплексной амплитуды электромагнитного поля 
от координаты x0 нарушителя:
. (4)
Полученное выражение является одномерным преобразованием Френеля функции 
, так как пара преобразований Френеля имеет следующий вид [5]: 
; 
,
где 
- функция переменной 
, а 
- её френелевский образ.
Обозначая в выражении (4) для 
и 
, в соответствии с первым из пары преобразований Френеля можно утверждать, что является френелевским образом функции 
при выполнении условий (3), поэтому в соответствии со вторым из пары преобразований Френеля можно положить:
. (5)
По аналогии с обратными преобразованиями Фурье и Френеля, выражение, восстанавливающее вид изменения зависимости одномерной функции пропускания Н, более общее, чем выражение (5), можно получить заменой в (2) на 
и показателя степени в экспоненте на комплексно сопряжённый, т.е.:
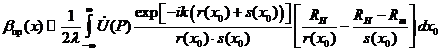. (6)
Полученное выражение можно использовать только для определения изменения (вида) функции пропускания объекта, так как она восстанавливается с точностью до множителя. Однако этого достаточно для целей определения размера Н по координате x. Использование его для восстановления функции пропускания по комплексной амплитуде для щели в плоском экране показало хорошие результаты определения её ширины 2а.
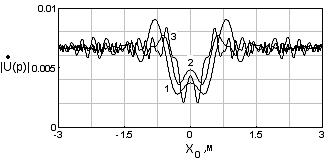
Больший интерес представляет использование выражения (6) для восстановления вида функции пропускания по координате X трёхмерных объектов. На рисунке 2а приведены результаты расчета значений 
по выражению (1) при размерах двух полуосей эллипса (см. рисунок 1) 
, 
и половиной высоты цилиндра 
, а на рисунке 2б - результаты восстановления вида функции βпр(x) при Rm=150 м; λ=0,016 м, A=1B для высоты размещения антенн ПРД и ПРМ h=y0 и равной 1м.
а) б)
Рисунок 2. Результаты расчета значений 
(рис. 2а) при Rн=75м для кривой 1, Rн=125м для кривой 2 и Rн=140 м для кривой 3 и восстановления функции пропускания βпр(x) (рис. 2б) по 
, соответственно для кривых 1 -3 рис. 2а
В соответствии с рисунком 2б размер Н 
по направлению X равен 
. Отметим, что значительные изменения высоты цилиндра b и координаты y0 его центра не приводят к заметному изменению определяемого размера 2a Н, хотя при этом наблюдаются существенные изменения модуля комплексной амплитуды 
.
Аналогичные результаты были получены и при восстановлении вида функции пропускания по координате x прямоугольных отверстий в плоском экране. Приведенные результаты определения размера нарушителя в направлении его перемещения показывают корректность использования выражения (6) при восстановлении функций пропускания одномерных, двумерных и трехмерных объектов.
2. Сравнение преобразования Френеля и Кирхгофа при восстановлении функции пропускания трехмерного объекта
Нетрудно проверить, что выражение (5) является частным случаем выражения (6) при условиях (3), вследствие чего преобразование (6) должно быть корректным в большей части диапазона изменения RH и 
. Однако преобразование Френеля применимо только при условиях (3), ограничивающих минимальные значения расстояний RH и Rm - RH соответственно от передающей и приемной антенн РЛТСО. При пересечении нарушителем ЗО РЛТСО вблизи антенн ПРД и ПРМ восстановление функции пропускания с использованием преобразования Френеля может оказаться неудовлетворительным. Вместе с этим, на преобразование (6) накладываются только ограничения применимости дифракционной формулы Френеля - Кирхгофа [2]:
и 
, (7)
где 
и 
- минимально допустимые значения расстояний Н от передающих и приемных антенн. Очевидно, что последние ограничения более слабые нежели (3). Поэтому, дополнительной проверкой сделанных при выводе преобразования (6) предположений и применимости его для восстановления функции пропускания могут послужить результаты восстановления βпр(x) с помощью выражения (6) и преобразования Френеля в широком диапазоне изменения RH и соответственно Rm-RH.
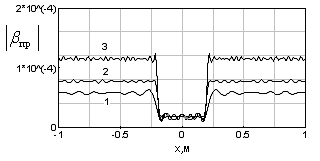
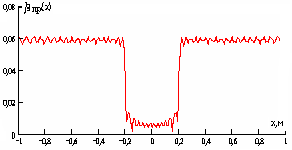
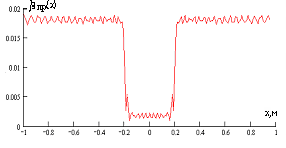
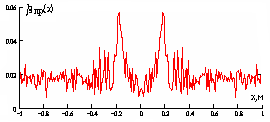
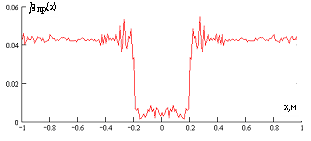
На рисунке 3 слева приведены результаты восстановления функции пропускания нарушителя βпр(x) с помощью обратного преобразования Френеля при размерах a=0,2м и Rm = 150m, а справа приведены результаты восстановления с помощью выражения (6). Значение расстояния RH Н от антенны ПРД равно 75 м и 146 м соответственно для рисунков а и б при неизменности остальных параметров расчета.
Рисунок 3. Результаты восстановления функции пропускания с помощью обратного преобразования Френеля (слева) и Кирхгофа (справа)
Графики восстановленных функций пропускания (без учёта значения βпр(x)) с помощью обоих преобразований практически одинаковы в диапазоне изменения RH от 75 до 145м. При RH =145м качество восстановления с помощью обратного преобразования Френеля ухудшается и при 
оно становится неприемлемым.
Так как дифракционный интеграл Френеля - Кирхгофа и выражение (6) симметричны относительно векторов 
и 
, а также их модулей, то результаты восстановления функции пропускания при расстоянии между антеннами 
для 
не будет отличаться от приведенных на рисунке 3б.
Приведённые результаты показывают, что при приближении Н к антеннам ПРД или ПРМ на расстояния 
или 
, нарушающих условия (3), прекращается восстановление βпр(x) с помощью обратного преобразования Френеля (5), при восстановлении в тех же условиях функции пропускания с помощью преобразования (6). Это приводит к уменьшению размеров "мёртвых" зон около антенн ПРД и ПРМ, в которых не возможно восстановление функции пропускания нарушителя, что является полезным эффектом преобразования (6). При дальнейшем уменьшении RH или Rm-RH и нарушении общего условия применимости дифракционной формулы Френеля - Кирхгофа прекращается восстановление функции пропускания и с помощью преобразования (6) .
Заключение
Предложенный алгоритм восстановления функции пропускания движущегося непрозрачного для электромагнитного поля нарушителя по его дифракционной картине позволяет уменьшить размеры "мертвых" зон вблизи антенн ПРД и ПРМ по сравнению с обратным преобразованием Френеля.
Рецензенты:
- Светлов А.В., д.т.н., профессор, заведующий кафедрой радиотехники и радиоэлектронных систем Пензенского государственного университета. г. Пенза.
- Бутаев М.М., д.т.н., профессор, ученый секретарь ОАО "НПП "РУБИН", г. Пенза.
Библиографическая ссылка
Чернышев М.Н., Сальников И.И., Чернышев Н.И. СРАВНЕНИЕ ОБРАТНЫХ ПРЕОБРАЗОВАНИЙ ФРЕНЕЛЯ И КИРХГОФА ПРИ ВОССТАНОВЛЕНИИ ОДНОМЕРНОЙ ФУНКЦИИ ПРОПУСКАНИЯ ОБЪЕКТА В ЗОНЕ ДЕЙСТВИЯ РАДИЛОКАЦИОННОЙ СИСТЕМЫ ОХРАНЫ // Современные проблемы науки и образования. – 2011. – № 6. ;URL: https://science-education.ru/ru/article/view?id=4961 (дата обращения: 20.04.2024).