Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Рябинин С.В. 1

---

1 Челябинский государственный педагогический университет

В статье рассматривается процесс создания математической модели профессионального выбора учащихся предпрофильных классов для последующего управления потоками учащихся в профильной школе. Прогнозирование и проектирование профессионального выбора с использованием математической модели рассматривается как вариант педагогического сопровождения профессионального самоопределения учащихся предпрофильных классов. Представлены результаты верификация разработанной модели. В ходе анализа профессионального самоопределения школьников на уровне микропроцесса, т.е. определения отдельной личностью своего выбора в мире профессий, был выявлен ряд факторов С помощью экспертной оценки (метод Делфи) факторы были оценены как прогностические и послужили для определения восемнадцати зависимостей, относящихся к категориям «экспертных знаний» и «фактов», которые легли в основу разработанной модели. Модель можно представить в виде графа. Она может быть использована как в предметной области «технология», так и во внеурочной деятельности для моделирования профессионального выбора учащихся предпрофильных классов.

Статья в формате PDF

140 KB

математическая модель

профессиональное самоопределение

профессиональный выбор

верификация модели

1. Гусинский Э.Н. Построение теории образования на основе междисциплинарного системного подхода. - М.: Школа, 1994. - 184 с.

2. Методы педагогических исследований / Под ред.А.И. Пискунова, Г.В. Воробьева. - М.: Педагогика, 1979. - 256 с.

3. ПЕДАГОГИКА: Большая современная энциклопедия / Сост. Е.С. Рапацевич. - Мн.: Соврем. слово, 2005. - 720 с.

4. Репин С.А. Образовательная деятельность и ее влияние на самоопределение личности // Вестник ЮУРГУ. Серия «Образование. Педагогические науки». Выпуск 10. - 2010. - № 36. - С.130-133.

5. Таха, Хемди А. Введение в исследование операций. - 7-е изд.: Пер. с англ. - М.: Издательский дом «Вильямс», 2005. - 912 с.

6. Федеральный образовательный государственный стандарт основного общего образования: [Утверждён приказом Министерства образования и науки Российской Федерации от 17 декабря 2010 г. №1897] // Министерство образования и науки РФ. - 2010.

7. Шамсутдинова, И.Г., Казарова, Е.Г. Психолого-педагогическая поддержка профессионального самоопределения учащихся / И.Г. Шамсутдинова, Е.Г. Казарова // Педагогика. - 2008. - №10. - С.62-69.

При этом малоисследованным остается процесс первичного самоопределения учащихся предпрофильных 8-9 классов, хотя, в соответствии с ФГОС, личностные результаты освоения ООП основного общего образования должны отражать «осознанный выбор учащегося и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений» [6].

Цель исследования: обоснование и разработка математической модели вероятностного прогнозирования профессионального выбора учащихся предпрофильных классов.

Материал и методы исследования. В понимании профессионального самоопределения школьников мы придерживаемся достаточно широкой точки зрения, согласно которой самоопределение рассматривается «как центральный механизм становления личностной зрелости, состоящий в осознанном выборе человеком своего места в системе социальных отношений» [4, с.130].

Самоопределение школьников не может быть стихийным процессом и предполагает его педагогическое сопровождение, которое основывается на взаимодействии педагога и ученика и способствует развитию субъектности учеников. Под психолого-педагогическим сопровождением мы, вслед за И.Г. Шамсутдиновой и Е.Г. Казаровой, понимаем «определенный арсенал методов, форм, средств, сопутствующих и способствующих более адекватному ПС» (профессиональному самоопределению)» [7, с.62-63].

Многие авторы включают в процесс педагогического сопровождения профессионального самоопределения школьников прогнозирование будущих планов, намерений, предпочтений и выборов ученика. Разделяя это мнение, мы сделали попытку разработать математическую модель профессионального выбора учащихся предпрофильных классов общеобразовательной школы. Рассмотрим процесс построения модели.

Э.Н. Гусинский отмечает, что часто к педагогическим системам применяют методы вероятностного моделирования, в частности, из-за принципа неопределенности для гуманитарных систем, согласно которому результаты взаимодействия и развития гуманитарных систем не могут быть детально предсказаны [1].

Понятия «моделирование» и «прогнозирование» в педагогике часто подразумевают один процесс, так понятие «вероятностного прогнозирования» трактуется как предвосхищение будущего на основе вероятностной модели, прошлого опыта и информации о наличной ситуации [3, с.47].

В нашей работе мы рассматриваем прогнозирование и проектирование профессионального выбора с использованием математической модели как вариант педагогического сопровождения профессионального самоопределения учащихся предпрофильных классов.

Вероятностное прогнозирование профессионального выбора учащегося мы определяем как средство педагогической поддержки профессионального самоопределения учащегося в процессе совместной выработки прогноза о возможном профессиональном выборе учащегося на основе математического моделирования с учетом внутренних и внешних факторов его профессионального самоопределения.

Для определения исходных оснований построения модели необходимо было выявить факторы профессионального самоопределения. С помощью историко-педагогического, социолого-педагогического и системного анализа был рассмотрен процесс профессионального самоопределения учащихся на уровне макро- и микропроцесса. На уровне макропроцесса, на основе анализа работ философов, социологов и экономистов,  были выявлены следующие факторы профессионального самоопределения школьников в современных условиях развития российского социума: экономические, социально-экономические, социально-педагогические.

В рамках социально-экономических факторов выявлены следующие зависимости и тенденции: зависимость доступности образования от материального положения семьи, зависимость между социальным и профессиональным статусом, зависимость уровня жизни и уровня образования от места проживания, зависимость между человеческим капиталом и образованием, зависимость образования и культурного капитала, изменение мотивов профессиональной деятельности населения.

При анализе профессионального самоопределение школьников на уровне микропроцесса, т.е. определения отдельной личностью своего выбора в мире профессий, были выявлены факторы:

• внутренние (психологические): знания, навыки, умения, привычки, которыми школьник овладевает в процессе жизнедеятельности; взгляды, убеждения, осознанное отношение, потребности, интересы, мотивы поведения, намерения личности;
• внешние социально-психологические: мнения родителей ученика, друзей, наличие семейных династий, традиций, влияние СМИ, значимость профессии на рынке труда, ее престижность, зарплата, др.;
• внешние педагогические: влияние целостного организованного педагогического процесса в школе на профессиональное самоопределение учащегося.

Наличие данных зависимостей мы проверили в ходе констатирующего эксперимента на контингенте 717 учащихся 9 классов 21 образовательного учреждения города.

Чтобы рассмотреть выявленные факторы как прогностические, т.е. определяющие процесс профессионального самоопределения школьников, мы прибегли к экспертной оценке, которая в научной литературе называется методом Делфи [2, с.112-137]. Пять экспертов, среди которых научно-педагогические работники, работники управления образованием, педагоги школ оценили баллами от 1 до 5 (1-высший балл) значимость основных факторов, к которым нами были отнесены социально-экономические, материальные, факторы личностного роста, психологические факторы возрастной группы, факторы среды первичной социализации, расположенные в определенном порядке. Для подтверждения правильности полученных выводов мы вычислили коэффициент конкордации, который показывает согласованность мнений экспертов. В нашем случае коэффициент конкордации W = 0,742, что означало сильную степень согласованности мнений экспертов.

Таким образом, эксперты не отвергли нашего вывода, подтвердили его, в силу чего мы рассматриваем далее выявленные факторы как прогностические, т.е. факторы, с помощью которых можно предвидеть, предсказать результат, в данном случае - профессиональных намерений и выбора учащихся.

Выявление перечисленных прогностических факторов послужило теоретическим основанием для построения математической модели, а именно для определения восемнадцати зависимостей, относящимся к категориям «экспертных знаний» и «фактов».

При этом зависимости из категории «экспертные знания» изначально задаются в модель в виде фактов, это происходит перед подготовкой к тестированию учащихся. К экспертным знаниям относятся:

• совпадение специальности родителей с их текущей профессией,
• уровень образования родителей,
• уровень дохода на члена семьи,
• условия проживания семьи.

Зависимости, относящиеся к категории «Факты», связаны между собой коррелирующим коэффициентом k, принимающим для каждой зависимости определённую степень двойки.

В ходе исследования нами были определены соответствующие приоритеты зависимостей при подстановке в модель. В таблице 1 зависимости расположены в порядке убывания приоритета и им присвоен уникальный идентификатор rn.

На основании приоритетов зависимостей нами был построен связный ациклический граф^[1] (т.н. «дерево», граф, который не содержит циклов, а между любой парой вершин существует ровно один путь). Данное дерево является бинарным (каждый узел имеет не более двух потомков и задаёт поддерево, корнем которого он является). Начальной вершиной является зависимость r14 «Совпадение интереса к предмету с успехами по предмету и выбранной профессией». Конечной вершиной в любом из поддеревьев является зависимость r1 «Участие в олимпиадах» (см. табл.1 и рис.1).

Таблица 1. Приоритеты зависимостей категории «Факты»

Также нами введена вероятностная переменная S, отвечающая за неопределённые величины (к примеру, учащемуся может перестать нравиться выбранный профиль). Такая переменная будет принимать какое-либо значение только в том случае, если был выбран путь B, поскольку полное совпадение интересов и успехов по предметам и профессиональных намерений учащегося практически полностью исключают вероятность подобного события. Более того, «успешные» ответы в узлах r13 и r12 на ветке B также будут являться исключающим событием для переменной S.

Определены следующие множества:

• множество событий A1, включает элементы r1, r3, r4, r6, r7 (незначительные факторы);
• множество событий B1, включает элементы r9, r10, r11 (значительные факторы);
• элементы r2, r5, r8 относятся к обоим множествам (к их пересечению U1), поскольку могут меняться в зависимости от неучтённых обстоятельств.

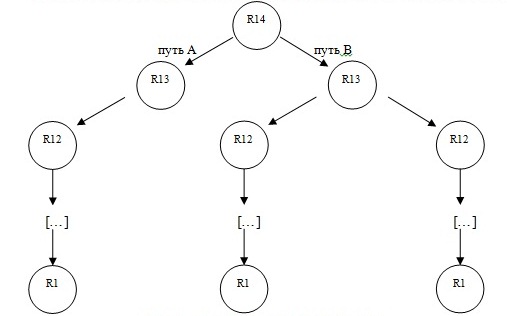
Рис.1. Дерево категорий «факты»

Возможность возникновения события S соотнесена с незначительными факторами (по данным нулевого среза, всего 6 % учащихся перестал нравиться выбранный ранее профиль). Если отмечено, по крайней мере, два значительных фактора из множества B, то это будет также исключающим событием для S.

Поэтому,  , где:

E - количество ожидаемых событий (одно),

N - общее количество равновероятностных событий (зависимостей rn) из множества A1 и пересечения множеств U1, которые были отмечены в ходе тестирования.

Если же выбран путь А, то определены следующие множества:

• множество событий A2, включает элементы r1..r8 (рассматриваются как незначительные факторы);
• множество событий B2, включает элементы r12, r13, r14 (значительные факторы);
• элементы r9, r10, r11 относятся к обоим множествам (к их пересечению U2).

Поскольку события множества A2 не могут существенно повлиять на конечный результат, то они могут не учитываться.

Поэтому,  , где:

E - количество отмеченных событий из множества B2.

Зависимости из категории «Экспертные знания», выделенные нами ранее, также дают дополнительную корреляцию для итогового значения. Эти четыре фактора являются теми данными, которые учащийся не может внести сам, и требуется непосредственное участие родителей в предварительном опросе, после которого данные должны быть учтены. Ранее нами было отмечено, что уровень образования родителей играет важную роль для их детей, так же как и материальное положение семьи. Также нами было отмечено, что несовпадение специальности родителей с их текущей профессией может существенно влиять на будущий выбор учащегося.

Нами были выбраны следующие коэффициенты (таблица 2).

Таким образом, нами была получена следующая модель вероятностного

Таблица №2. Приоритеты зависимостей категории «Экспертные знания»

прогнозирования профориентационного выбора учащихся:

 , где:

, ,  - число зависимостей, относящихся к категории «Факты»,

S - вероятностная переменная, в зависимости от решения графа, рассчитываемая по формуле  или .

Построенная модель нуждалась в верификации (удостоверении в подлинности). Согласно Х.А. Таха, проверка адекватности модели предполагает проверку ее правильности: «формальным общепринятым методом проверки адекватности модели является сравнение полученного решения (поведение модели) с известными ранее решениями или поведением реальной системы. Модель считается адекватной, если при определенных начальных условиях ее поведение совпадает с поведением исходной системы при тех же начальных условиях» [5, с.30].

Данная модель прошла верификацию в 2011 году в трёх школах г.Челябинска. В качестве экспериментальных групп выступали профильные классы следующих общеобразовательных учреждений: гуманитарная гимназия (25 учащихся, ЭГ-1) и лицей с информационно-технологическим уклоном (18 учащихся, ЭГ-2). Контрольная группа (21 учащийся средней общеобразовательной школы) позволяла увидеть поведение исходной системы при тех же начальных условиях.

На раннем этапе построения модели нами был сделан прогноз выбора учащимися дальнейшего пути образования в профильном классе. Для ЭГ-1 этот прогноз равнялся 40,3 % (25 человек из числа учеников 9 классов), однако был разделен на профили филологический (20 % - 5 человек), гуманитарный (32 % - 8 человек) и социально-гуманитарный (12 человек - 48 %) соответственно.

Для ЭГ-2 прогноз составил 100 % - 21 человек (на момент первоначального тестирования), однако в этой группе был большой разброс выбираемых профилей обучения: экономический - 3 (14, 29 %), физико-математический - 3 (14, 29 %), индустриально-технологический - 3 (14, 29 %), информационно-технологический (ИТ) - 3 (14, 29 %), гуманитарный - 2 (9, 52 %), филологический - 1 (4, 76 %), химико-биологический - 2 (9, 52 %), социально-гуманитарный (правовой) - 1 (4, 76 %), оборонно-спортивный - 3 (14, 29 %). Заранее было понятно, что школа не сможет предоставить такое разнообразие профилей ученикам, и в силу того, что большую часть учеников можно было объединить, их направили в ИТ-профиль.

После реального выбора учащимися профиля обучения была проведена проверка истинности их намерений в 10 классе.

Как видно из рисунка 2, желание учиться в профильной школе не совпадает у достаточно большой части учеников (61,11 %) с выбором конкретного профиля.

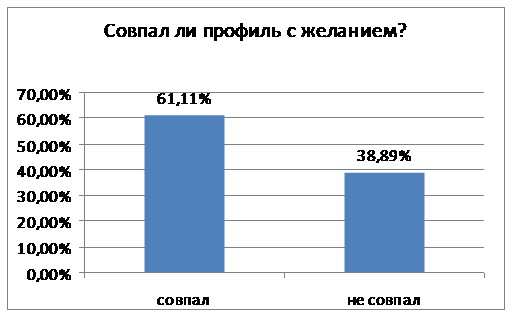
Рис. 2. Совпадение фактического выбора учащимися ЭГ-2 с намерениями

В соответствии с прогнозом в этот профиль могли пойти учиться 57,14 % учащихся, что практически и подтвердилось в 10 классе. В данном случае школа не предоставила возможности выбора учащимся (в школе только один 10 класс) в связи с небольшим количеством учащихся, а ученики не захотели по каким-либо причинам сменить школу.

В ЭГ-1 показатели соотношения намерений и фактического выбора лучше - большинство учеников в соответствии с прогнозом выбрали профильный класс, т.к. в школе гуманитарная направленность обучения и различия в предметных областях не столь существенны, как в лицее (рис.3).

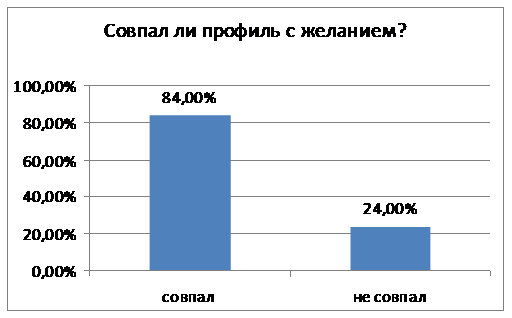
Рис. 3. Совпадение фактического выбора учащимися ЭГ-1 с намерениями

В обеих группах в целом 66, 67 % учащихся в дальнейшей жизни будут придерживаться выбранного профиля обучения. Однако только 55, 56 % из них собираются продолжить образование, остальные 11,11 % думают уже сейчас о трудоустройстве. Обратим внимание на то, что у 61, 11 % выбор этого профиля совпал с желанием. Можно также отметить, что желание придерживаться выбранного профиля уменьшается по мере обучения.

Результаты исследования. На основании выявленных данных (в т.ч. представленных выше) можно сделать следующий вывод:

• отмечается несоответствие выбранного профиля обучения и реальных желаний учащихся,
• значительное количество учеников, обучающихся в выбранном профиле, изменяют свое представление о возможном выборе профессии,
• обучение в выбранном профиле не подкрепляется активностью учащихся как во внеурочной познавательной деятельности в школе, так и во внешкольной познавательной деятельности,
• значительная часть учащихся готовы сменить как предполагаемую профессию, так и профиль образовательного учреждения,
• произошла резкая смена структуры мотивов выбора предполагаемой профессии, на первое место вышли мотивы материальные, на второе - социально обусловленные, мотивы личностного роста заняли третье место по значимости.

Таким образом, значительная часть учеников профильных классов по различным показателям от 55 до 76 % проявляют неустойчивость профессиональных намерений, что свидетельствует об отсутствии эффективности процесса профессионального самоопределения в предпрофильных классах, так как именно в 9 классе учениками был сделан выбор, к которому они оказались не готовыми в 10 классе.

Итак, второй срез подтвердил сделанный нами с помощью математической модели вероятностный прогноз намерений учащихся в продолжении обучения в профильном классе. Для подтверждения этого вывода мы использовали критерий χ2 «хи-квадрат» К. Пирсона, наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Нашей задачей было проверить, отличаются ли полученные эмпирические данные от теоретически равновероятных. Поскольку полученное эмпирическое значение (χ²= 104,5625) больше критического (χ² = 11,07), это говорит о том, что различия частот достоверны.

Заключение. Верификация модели прошла успешно и доказала возможность использования вероятностного прогнозирования профессионального выбора учащихся к обучению в профильном классе с помощью математической модели в рамках педагогического сопровождения профессионального самоопределения школьников предпрофильных классов.

Разработанная нами математическая модель может быть использована как в предметной области «технология», так и во внеурочной деятельности. Также разработано программное обеспечение, реализующее данную модель. Подобная модель предоставляет возможность для руководителей общеобразовательных учреждений района и города управлять потоками учащихся предпрофильных классов для последующего грамотного комплектования профильных классов, в которых бы в большей мере учитывались интересы и возможности обучающихся.

Рецензенты:

• Волчегорская Е.Ю., д.п.н., профессор, зав. кафедрой педагогики, психологии и предметных методик ФГБОУ ВПО «Челябинский государственный педагогический университет», г. Челябинск.
• Попова А.А., д.п.н., профессор, зав. кафедрой математики, естествознания и методики преподавания математики и естествознания ФГБОУ ВПО «Челябинский государственный педагогический университет», г. Челябинск.

[1] Граф - совокупность непустого множества вершин и множества пар вершин. Объекты представляются как вершины, а связи - как дуги или рёбра.

Библиографическая ссылка