Введение и постановка задачи
Задачу аппроксимации дискретных данных, содержащих как нормальные, так и аномальные шумовые выбросы, сформулируем в одномерной постановке. Пусть имеется исходная дискретная функциональная зависимость 
, где 
, описывающаяся линейным законом:
(1)
где 
, 
– исходные значения параметров зависимости (1).
Предположим, что при экспериментальном построении функциональной зависимости 
система регистрации и/или наблюдения подвержена влиянию случайных искажений – как нормального гауссовского шума 
с нулевым математическим ожиданием 
и небольшой дисперсией 
так и аномальных помех импульсной (аппликативной) структуры.
В результате наблюдаемая последовательность экспериментальных данных описывается моделью:
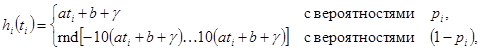(2)
где 
– вероятности возникновения нормальных ошибок при измерении величины в 
-х моментах времени 
; 
– функция генерирования случайного значения зависимости 
на интервале 
с равномерным распределением случайной величины.
В качестве примера на рис. 1 приведена одна из реализаций модели наблюдения (2) для случая, когда вероятности (2) изменяются с течением времени по закону 
.
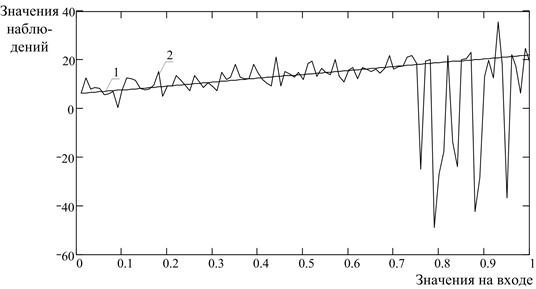
Рис. 1. Исходная линейная зависимость (1) и ее деградация (2) в результате воздействия нормально-аномальных помех
Как видно из рис. 1, в результате воздействия аномальных импульсных помех (2) на нормальную смесь 
, последняя утратила свойство стационарности во времени 
.
Задачу сформулируем в виде, отличающемся от классического метода наименьших квадратов (МНК) [5]. Необходимо найти вектор таких значений оценок 
и 
параметров и (1), которые являлись бы аргументами минимума:
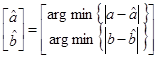(3)
Особенности нейросетевой аппроксимации нестационарных данных
Для решения сформулированной задачи (3) может быть использован аппарат адаптивных линейных нейронных сетей (НС), т.е. сетей с линейными функциями активации.
Адаптивная нейронная система представляет собой линейный сумматор, основным свойством которого является изменяющееся во времени функционирование с саморегулированием [7]. Если сигнал подается на вход системы для определения свойств по ее отклику, то система адаптируется к этому определенному входному сигналу и тем самым изменяет собственную параметрическую организацию [7].
В адаптивной нейронной системе вектор весов 
зависит от выходного сигнала, а также от полезного отклика или обучающего сигнала 
.
В процессе обучения вектор весов самонастраивается таким образом, чтобы на 
-м шаге выходной сигнал нейронной сети 
имел наилучшее соответствие полезному отклику 
. Для этого выходной сигнал сравнивается с полезным откликом, на основе чего вырабатывается сигнал ошибки, корректирующий вектор весов на каждом шаге итерации. Для решения задачи аппроксимации в одномерной постановке (3) достаточно использования единственного адаптивного нейрона с двумя входами и линейной функцией активации.
В этом случае для нейрона формируется функционал ошибки 
, имеющий, как правило [1, 7] квадратичный вид:
, (4)
где 
– выход нейрона, описывающийся выражением:
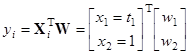, (5)
где 
– двухкомпонентный входной вектор, 1-я компонента которого представляет собой время наблюдения 
(2), а вторая – единичный вход; – 2-х компонентный вектор весов, соответствующий .
Подставив (5) в выражение функционала ошибки (4), имеем:
. (6)
При использовании методов обучения 1-го порядка (градиентных методов), правило самонастройки вектора весов вытекает из градиента функционала ошибки по настраиваемым параметрам – весам. В нашем случае компоненты градиента функционала ошибки (6) примут вид:
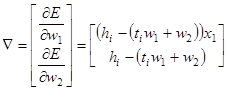. (7)
Поскольку значения компонентов вектора весов на 
-м шаге обучения должны изменяться в направлении антиградиента ошибки, правило их самонастройки будет иметь вид:
, (8)
где 
– новое значение вектора весов; 
– текущее значение весов; 
– параметр, определяющий приращения, от которых зависит устойчивость и скорость сходимости алгоритма обучения.
В частности, как показано в [7], в случае стационарных обучающих пар «
» условие сходимости алгоритма выполняется, если значение параметра 
удовлетворяет неравенству:
, или 
, (9)
где 
– максимальное собственное значение корреляционной матрицы 
входного сигнала; 
– след (сумма диагональных элементов) матрицы .
К сожалению, для рассматриваемого нестационарного случая в виде нормально-аномальной модели (2) правило (9) не подходит, и выбор параметра должен осуществляться экспериментально. Как показали численные исследования, в данном нестационарном случае может быть использован адаптивный выбор величины параметра [1]:
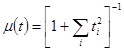. (10)
В работе [2] указано, что решение задачи аппроксимации данных, зашумленных нормальным шумом , адаптивным линейным нейроном (4)-(8) и классическим МНК дает приблизительно одинаковые значения параметров 
и . Вместе с тем, в случае, когда аппроксимируемые данные описываются нормально-аномальной моделью (2), точностные характеристики МНК и линейного нейроэлемента (4)-(8) различаются достаточно сильно. В частности, установлено, что аномальные выбросы (на рис. 1 – в точках 
) сильно влияют на оцениваемые по МНК параметры 
и 
, поэтому точность МНК падает. В тоже время установлено, что точность оценивания параметров 
и 
с использованием линейного нейрона зависит прежде всего от положения аномальных измерений в выборке. Так, для наблюдения рис. 1 абсолютные ошибки оценивания параметров составили: для МНК – 
, 
; глобальной численной оптимизации – 
, 
; адаптивного линейного нейрона – 
, 
. Видно, что точность оценивания параметров в данном случае выше у МНК и метода глобальной численной оптимизации. Оценки параметров, даваемые последними двумя методами, в каждом случае совпадают, поэтому остановимся на сравнении адаптивного линейного нейроэлемента с классическим МНК.
Для наблюдения, аналогичного рис. 1, но с аномальными помехами, находящимися в точках первой половины выборки (
), типичные абсолютные ошибки оценивания составляют: 
, 
, 
, 
.
Метод и алгоритмы кортежирования обучающей выборки для повышения точности нейросетевой аппроксимации данных
Анализ применимости известных методов к задаче аппроксимации нестационарных данных позволил сделать важный вывод, заключающийся в том, что для снижения абсолютных ошибок оценивания параметров, обучение адаптивного линейного нейрона должно начинаться с аномальных измерений и заканчиваться на нормальных. В случае, когда аномальные измерения имеют место в начальных точках времени наблюдения (2), обучение нейрона начинается с этих аномальностей, поэтому использование метода кортежирования не требуется. Если аномальности находятся в конечных точках временного интервала наблюдения (рис. 1), либо равномерно распределены на этом интервале, снизить абсолютные ошибки оценивания параметров возможно на основе формирования определенной последовательности обучающих пар (вход – выход ), такой, при которой сначала следуют аномальные измерения (в порядке снижения своей «аномальности»), а затем – нормальные. При этом последовательность обучающих пар, сформированную по указанному выше правилу, будем называть кортежем обучающей выборки (кортеж – упорядоченный по определенному правилу набор, конечная последовательность каких-либо объектов) [4].
В качестве метода кортежирования обучающего множества (т.е. формирования кортежей обучающих пар) в условиях сформулированной в виде (1)-(3) задачи, можно использовать построение вариационных рядов локальных отклонений от наблюдений 
(2) и рядов аналогов производных – локальных конечных разностей [6]. В первом случае алгоритм кортежирования обучающей выборки будет иметь следующий вид [6].
Алгоритм 1.
Шаг 1. Вычисление нормированных локальных отклонений каждого измерения
(2):
, (11)
где символ 
означает математическое ожидание наблюдения .
Шаг 2. Построение вариационного ряда (в порядке убывания) локальных отклонений 
, вычисленных на шаге 1:
, 
. (12)
Шаг 3. Построение обучающих пар из последовательности в новую последовательность (кортеж) 
, соответствующую вариационному ряду 
(12).
Таким образом, после применения алгоритма 1 обучение адаптивного линейного нейрона будет начинаться с обучающих пар, имеющих наибольшую дисперсию (т.е. аномальность) и заканчиваться на парах с наименьшей дисперсией.
Во многих практических приложениях значения 
(11) определить не представляется возможным, например, доступна только одна реализация наблюдений . В этом случае для построения алгоритма кортежирования можно использовать аналоги производной – локальные конечные разности. При этом алгоритм будет иметь следующий вид [6].
Алгоритм 2.
Шаг 1. Вычисление значений квадратов локальных конечных разностей (1-го порядка) наблюдений :
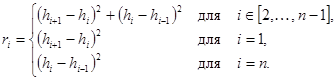(13)
Шаг 2. Построение вариационного ряда (в порядке убывания квадратов конечных разностей 
(13), вычисленных на шаге 1:
, 
. (14)
Шаг 3. Перестроение обучающих пар из последовательности в кортеж , соответствующий вариационному ряду 
(14).
Результаты численного моделирования предлагаемого метода
На рис. 2 и 3 приведены поверхности ошибок, а также траектории движения весов нейрона при его обучении на нормально-аномальных наблюдениях (рис. 1) без алгоритмов кортежирования (рис. 2) и с алгоритмом кортежирования (13)-(14) (рис. 3).
а)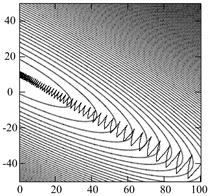
б)
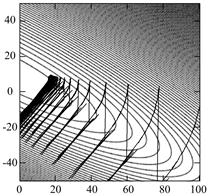в)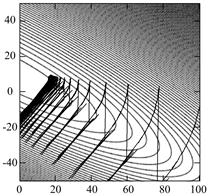
Рис. 2 Траектории весов нейрона на поверхности ошибок без использования алгоритмов кортежирования: а – недорегулированный процесс, (
); б – перерегулированный процесс, (
); в – адаптивный шаг (10)
В случае, представленном на рис. 2, абсолютные величины ошибок аппроксимации составили: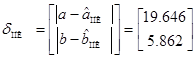 
, 
, 
, 
.
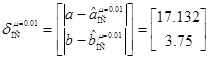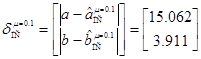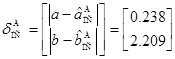а)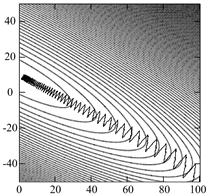
б)
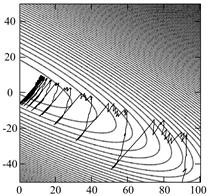в)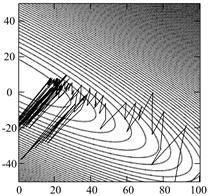
Рис. 3 Траектории весов нейрона на поверхности ошибок при использовании алгоритма кортежирования:
а – недорегулированный процесс, (); б – перерегулированный процесс, (); в – адаптивный шаг (10)
В случае, представленном на рис. 3, абсолютные величины ошибок аппроксимации составили: ,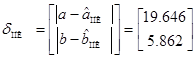 
, 
, 
.
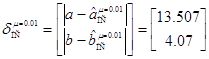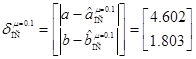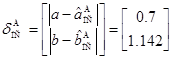Заключение
В работе выявлена важная особенность аппроксимации нестационарных данных моделью однослойной линейной нейронной сети. Эта особенность заключается в том, что точность оценивания искомых параметров аппроксимируемой зависимости существенно зависит от положения аномальных данных на интервале наблюдения. В случае, когда аномальные данные преобладают на начальном интервале наблюдения, а на остальном – нормальные, адаптивная линейная нейронная сеть позволяет получить более точные оценки искомых параметров по сравнению с классическим МНК. И наоборот, если аномальные данные присутствуют на конечном интервале наблюдения, нейронная сеть проигрывает по точности МНК. Указанная особенность позволила разработать метод кортежирования обучающих данных, заключающийся в их предварительной перетасовке в обучающей выборке по правилу убывания степени нестационарности.
Исследование проведено при поддержке Министерства образования и науки Российской Федерации, соглашение 14В37.21.2067
Рецензенты:
Елисеев Александр Вячеславович, доктор технических наук, доцент, профессор кафедры "Радиоэлектроника", Минобрнауки России, Ростовский технологический институт сервиса и туризма (филиал) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса», г. Ростов-на-Дону.
Мищенко Сергей Евгеньевич, доктор технических наук, профессор, ведущий научный сотрудник, Федеральное государственное унитарное предприятие "Ростовский научно-исследовательский институт радиосвязи" Федеральный научно-производственный центр, г.Ростов-на-Дону.
Библиографическая ссылка
Челахов В.М., Деркачев К.В. МЕТОД КОРТЕЖИРОВАНИЯ ОБУЧАЮЩЕЙ ВЫБОРКИ ДЛЯ ПОВЫШЕНИЯ ТОЧНОСТИ НЕЙРОСЕТЕВОЙ АППРОКСИМАЦИИ ДАННЫХ // Современные проблемы науки и образования. – 2012. – № 6. ;URL: https://science-education.ru/ru/article/view?id=7869 (дата обращения: 18.04.2024).