Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Аксенов Б.Г. 1 Фомина В.В. 1 Липихин А.С. 1

---

1 ФГБОУ ВПО "Тюменский государственный архитектурно-строительный университет"

В данной работе рассматривается метод построения сужающейся системы оценок решения задачи теплопроводности с немонотонными граничными условиями, которая описывает процесс теплообмена с фазовым переходом во влажном дисперсном грунте. Решение имеет вид системы функций, поочередно мажорирующих искомое решение сверху и снизу. Оценки находятся с помощью теорем сравнения для уравнений параболического типа. Теоремы сравнения называют также теоремами монотонности, так как монотонность – естественное условие их применения. В данной работе рассматриваются задачи с немонотонными граничными условиями, вследствие чего немонотонной является сама искомая функция. Разработаны искусственные приемы, позволяющие заменить немонотонные функции определенной комбинацией монотонных, после чего удается применить теоремы сравнения, либо интегральные неравенства для построения границ решения. Приводится эффективная процедура численной реализации данного метода. Проведен численный анализ решения тестовой задачи.

Статья в формате PDF

162 KB

оценки

немонотонные граничные условия

задача теплопроводности

фазовый переход

влажные грунты

1. Аксенов Б. Г., Фомина В. В. Решение осесимметричных задач тепломассообмена с фазовым переходом во влажных дисперсных материалах // Доклады АН ВШ РФ. – Новосибирское отделение АН ВШ. – 2012. – № 1(18). – С.44-52.

2. Даниэлян Ю. С. Приближенное решение температурных задач нелинейной теплопроводности с тепловыделением в спектре температур // Изв. СО АН СССР. Сер. тех. наук. – 1982. – Вып. 2. – № 8. – С. 6-12.

3. Даниэлян Ю. С., Аксёнов Б. Г. Построение оценок решений некоторых немонотонных задач нелинейного теплообмена. – Изв. РАН. ТВТ. – 1985. – Т. 23. – N. 5. – С. 904-909.

4. Коллатц Л. Функциональный анализ и вычислительная математика. – М.: Мир, 1969. – 448 с.

5. Мирзаджанзаде А. Х. и др. Термовязкоупругость и пластичность в нефтепромысловой механике. – М.: Недра, 1973. – 324 с.

6. Тихонов А. Н. Об остывании тел при лучеиспускании, следующем закону Стефана – Больцмана // Изв. АН СССР. География и геофиз. – 1973. – № 2. – С. 461-479.

7. Тихонов А. Н., Самарский А. А. Уравнения математической физики. – 4-е изд., испр. – М.: Наука, 1972. – 736 с.

Введение

После того, как Вестфалем были доказаны теоремы сравнения для уравнения параболического типа [4], появилось несколько работ, использующих эти теоремы для приближенных решений нелинейных задач теплопроводности [5]. Но еще значительно раньше, фактически на том же принципе построено решение задач с нелинейным граничным условием А. Н. Тихоновым [6]. Решение имеет вид системы функций, поочередно мажорирующих искомое решение сверху и снизу. Такие функции С. А. Чаплыгин (1976) называл «границами»: он использовал их для решения обыкновенных дифференциальных уравнений. Работа [6] и послужила источником вдохновения для построения границ решений довольно широкого класса прикладных задач, о которых речь ниже.

Л. Коллац назвал теоремы сравнения теоремами монотонности, так как монотонность – естественное условие их применения. В 1982 году Ю. С. Даниэлян [2] построил границы (оценки) решения монотонной задачи с немонотонными коэффициентами. В данной работе рассматриваются задачи с немонотонными граничными условиями, вследствие чего немонотонной является сама искомая функция.

Некоторые искусственные приемы помогают заменить немонотонные функции определенной комбинацией монотонных, после чего удается применить теоремы сравнения, либо интегральные неравенства для построения границ решения.

Постановка задачи

Решается задача

(1)

(2)

Эта задача описывает процесс теплообмена с фазовым переходом во влажном диспесном или пористом материале (грунт, строительный материал). Здесь – соответственно температура, теплоемкость, коэффициент теплопроводности, время, пространственная координата, содержание незамерзшей влаги, скрытая теплота замерзания воды в грунте, – дифференцируемая функция с ограниченной вариацией: , М – положительная константа,

, где – это экспериментально определяемая зависимость.

Подстановки Кирхгофа и Голанта приводят уравнение (1) к виду

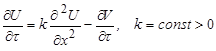(3)

где – некоторые функции от .

Заменой искомой функции легко добиться также, чтобы начальное условие было нулевым. Будем считать, что все эти преобразования уже проведены. Чтобы не вводить новых переменных, положим в (1), (2) и получим уравнение

(4)

где с условиями:

(5)

Уравнение (4) имеет такой же вид, как и уравнение (3), к которому приводится (1). Получаемые в результате преобразований условия аналогичны (5). Поэтому вместо задачи (1)–(2) в дальнейшем рассматриваем задачу (4)–(5). Функция по своей физической природе является неубывающей. Производная может быть как непрерывной унимодальной функцией, так и имеющей особенность типа дельта-функции. Во втором случае (4)–(5) является одной из форм записи фронтовой задачи Стефана. Здесь же считаем, что есть непрерывная дифференцируемая функция. Такая ситуация характерна для тонкодисперсных грунтов, тогда как явно выраженный фронт образуется в грунтах крупнозернистых.

Решение ищем в классе непрерывных функций при .

Обоснование метода решения

Если непрерывная дифференцируемая функция, то ограниченная функция и вместо (4) можно записать

или

(6)

где .

В уравнении (6) - немонотонный коэффициент, кроме того, немонотонной является функция , вследствие чего немонотонна и искомая . Используя теоремы сравнения [4], можно доказать следующее утверждение.

Если заданы функции , являющиеся решениями следующих задач:

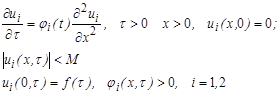
причем то при неубывающей и положительной , а при невозрастающей и отрицательной .

Построение границ решения

Для построения решения задачи (4)–(5) функцию представим в виде

(7)

где – неубывающая положительная функция, – невозрастающая отрицательная функция. Можно доказать, что , если удовлетворяют уравнениям:

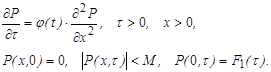(8)

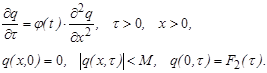
причем из (8) следует, что .

Границы найдем из уравнений

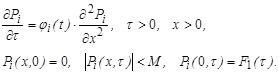(9)

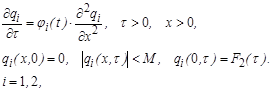
(10)

– соответственно наименьшее и наибольшее значения . Так как и учитывая (7), находим границы

Решения задач (9) легко находятся в аналитическом виде [6]. Используя , строим оценки , такие, что Предположим, что функция от такая, что После необходимых преобразований решение уравнения (4) с условиями (5) получаем в виде:

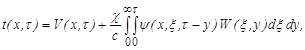(11)

где

;

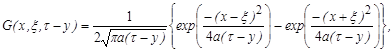– функция Грина,

,

– решение уравнения с условием вида (5).

Далее определим функции следующим образом:

(12)

.

Очевидно, что

. (13)

Используя полученные границы , получим функции , согласно (11), в виде следующих выражений:

(14)

Так как – монотонно возрастающая функция, то из выражений (12)–(13) имеем. Используя аналогично (14) получаем и т.д. Для границ имеем формулы

(15)

Итерационная процедура (10) равномерно сходится в произвольном интервале , если в качестве границ использовать функции

. (16)

Тогда при четном i:

Эффективный метод численной реализации

Вычисление по формулам (15), (16) проводим на ПК с дискретизацией по , однако для каждого набора вычисления приходится проводить заново, так как интеграл, содержащий параметры, не является аддитивным. Кроме того, возникает необходимость хранения в памяти двумерных массивов, содержащих значения предыдущих границ в узлах дискретизации. Обе эти трудности снимаются, если применить дискретизацию по времени уже на этапе постановки краевой задачи, учитывая, что исходный дифференциальный оператор аддитивен по времени. Вместо (4), (5) можно, выбрав шаг дискретизации , записать:

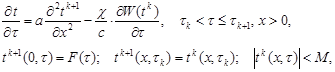(17)

где k=1,2,3,…; .

При такой постановке результат решения на предыдущем отрезке является начальным условием для последующего отрезка, причем если .

Процедуру уточнения оценок по формулам вида (15)–(16) проводим на каждом отрезке до получения необходимой точности, а затем переходим к следующему этапу, считая, что на предыдущем получено практически точное решение. Если , то автоматически обеспечивается сходимость процесса.

На каждом проводим дискретизацию по (и по ) с шагом . При фиксированном в прямоугольнике , величину усредняем и считаем постоянной, равной , где – среднее значение температур по четырем узловым точкам на предыдущей итерации. Тогда, по свойствам непрерывных функций, существует внутри прямоугольника некоторая точка , для которой эту постоянную величину можно вынести за знак интеграла. Тогда ее можно вынести за знак интеграла. После необходимых преобразований получаем при четном :

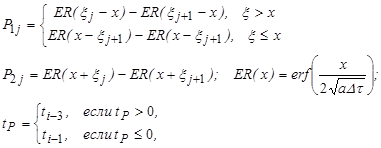
– решение задачи вида (17) для однородной части уравнения; – количество шагов дискретизации.

Заметим, что функции ER не зависят ни от момента времени, ни от номера границы, поэтому их вычисляют один раз и хранят в памяти в виде массива.

Численный анализ решения задачи теплопроводности

В качестве примера в работе решена задача на плоскости с условиями

, .

для граничной функции вида и при следующей зависимости

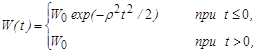
где – коэффициент формы кривой. Были приняты значения исходных данных:

В таблице приведены оценки значений температуры для различных значений в разных приближениях.

Оценки температуры для тестовой задачи

В этом случае решение можно получить с любой необходимой точностью, которая гарантируется наличием верхней и нижней оценок. Для данного примера при числе итераций 19 верхние и нижние оценки практически сливаются (разность не превышает ).

В связи с отсутствием точных аналитических решений задач вида (1)–(2), было проведено сравнение с прямым численным счетом по методу Самарского [7]. Получено практически полное совпадение с 19-м приближением при правильном подборе параметров численной схемы.

Выводы. Получено решение задачи (1)–(2) в виде сужающейся системы оценок искомой функции сверху и снизу. В итоге, может быть достигнута любая заданная точность результата.

Предлагаемый метод может использоваться в инженерных расчетах. А также в качестве эталонного для оценки точности численных и приближенных методов.

Метод, после необходимой модификации, может применяться для задач вида (1)–(2) во всех пространственных областях, для которых известны функции Грина. Очевидно, например, что можно решать задачу в одномерной цилиндрической области. В прикладном отношении это – решение задачи промерзания – оттаивания вблизи трубопровода [1] или нефтяной (газовой) скважины.

Рецензенты:

Чекардовский Михаил Николаевич, доктор технических наук, профессор, зав. кафедрой теплогазоснабжения ФГБОУ ВПО «ТюмГАСУ», г. Тюмень.

Степанов Олег Андреевич, доктор технических наук, профессор, зав. кафедрой промышленной теплоэнергетики ФГБОУ ВПО «ТюмГАСУ», г. Тюмень.

Грызлов Владимир Сергеевич, доктор технических наук, профессор, профессор кафедры «Строительных технологий и экспертизы недвижимости», ГОУ ВПО Череповецкий государственный университет, г. Череповец.

Библиографическая ссылка