Грохочение предназначено для разделения продуктов по классам крупности путем просеивания через одно или несколько сит. Осуществляется данный процесс при помощи вибрационного грохота, представляющего собой колебательную систему из двух масс: короба и опорной рамы, связанной с ним упругими элементами. На коробе установлена плоская рабочая поверхность, имеющая отверстия, на которой осуществляется процесс рассеивания материала по классам крупности.
Анализ работы вибрационных грохотов показал, что наклон плоскости рабочей поверхности существенно влияет на эффективность грохочения [2; 3].
Для исследования влияния угла наклона рабочей поверхности составлена математическая модель поведения частиц горных пород на поверхности пассивного (без колебаний) грохота, включающая уравнения свободного полета рудной частицы и ее удара о наклонную плоскость.
Если частица брошена вниз на неподвижную поверхность наклонного грохота без начальной скорости c высоты h, то при отсутствии сопротивления воздуха в момент удара о поверхность
, (1)
где 
- ускорение свободного падения, 
м/с2.
Частица при этом падает вертикально, и поэтому в момент соприкосновения с наклонной плоскостью вектор скорости падения V0 составляет угол φ с нормалью к этой плоскости, равный углу наклона плоскости рабочей поверхности. Таким образом, при первом ударе частицы о плоскость угол падения 
. Величину скорости после удара 
и угол отражения 
при произвольном ударе «i» можно найти из системы уравнений, определяющих коэффициенты восстановления и трения при ударе, а также уравнений теоремы об изменении количества движения [1]:
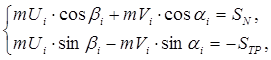(2)
где 
– масса частицы, кг; 
– составляющие ударного импульса, Нс; 
– скорость частицы перед i- м ударом о рабочую поверхность, м/с (рис. 1).
При этом коэффициент восстановления равен
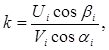, (3)
а коэффициент трения при ударе определяется в соответствии с гипотезой Рауса [1]:
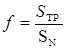. (4)
Решая систему уравнений (2) - (4), получаем
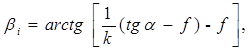, (5)
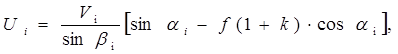. (6)
После отражения частицы от поверхности грохота происходит ее свободный полет. Если пренебречь силами сопротивления движению, уравнения свободного полета в системе координат, связанной с наклонной поверхностью грохота, можно получить из соотношений кинематики равнопеременного движения [1]: так как 
то эти уравнения имеют вид
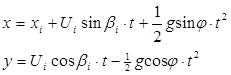, (7)
где t - текущее время:
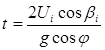. (8)
Дальность полета 
вдоль поверхности грохота до следующего удара находим, исключив из системы уравнений (7) параметр t при условии, что y=0:
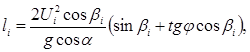. (9)
Проекции скорости частицы в момент следующего удара определяем дифференцированием уравнений (7):
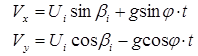. (10)
для t, определяемого уравнением (8), угол падения при этом составит:
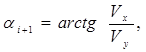. (11)
а величина скорости падения:
. (12)
После отражения частицы от поверхности грохота происходит ее свободный полет, затем снова удар и т.д. Если при этом при одном из ударов угол падения меньше некоторого критического 
, произойдет проваливание частицы сквозь решетку грохота.
Критический угол можно определить в соответствии с рис. 2 по формуле:
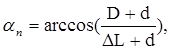. (13)
где D - диаметр частицы, м; d - диаметр прута решетки, м; 
- ширина щели решетки грохота, м.
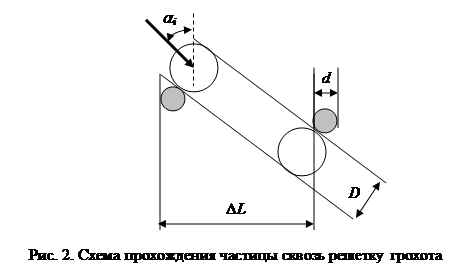
Весь процесс многократного чередования свободного полета с ударами до прохождения частицы сквозь решетку возможно смоделировать на компьютере. При этом, варьируя начальные условия и другие переменные, возможно подобрать наиболее рациональные параметры установки.
Численные расчеты по приведенным формулам проведены для величин коэффициентов восстановления и трения при ударе горных пород, приведенных в работе [5]. Модель учитывает также и возможность перекатывания частиц по рабочей поверхности с учетом трения качения [4].
Результаты расчетов для усредненных значений k=0,47, f=0,09 (удар о стальную поверхность) приведены в табл. 1.
Результаты расчетов кинематических параметров
рудных частиц при ударе о рабочую поверхность грохота
Таблица 1
|
φ, град. |
№ удара |
α, град. |
V, м/с |
β, град |
U, м/с |
l,м |
|
h=0,25м |
||||||
|
5 |
0 1 |
5 4.6 |
2,21 |
-5,1 |
1,1 |
-4*10^-4 |
|
15 |
0 1 2 3 |
15 39,6 63,6 77,6 |
2,21 1,29 1,05 1,02 |
16 56 76 84 |
1,04 0,83 0,91 0,97 |
0,12 0,08 0,04 0,02 |
|
30 |
0 1 2 3 |
30 64,9 78,9 85,5 |
2,21 2,08 2,30 2,43 |
44 76 85 88 |
1,23 1,81 2,21 2,40 |
0,28 0,21 0,10 0,05 |
|
h=0,5м |
||||||
|
15 |
0 1 2 3 |
15 39,6 63,6 77,6 |
3,13 1,83 1,49 1,45 |
16 56 76 84 |
1,48 1,18 1,29 1,38 |
0,24 0,16 0,08 0,04 |
Анализируя приведенные результаты, можно заметить, что значения углов падения при очередных ударах не зависят от высоты h, с которой происходит загрузка материала. При этом, если не произошло просеивания частицы под решетку грохота, то вероятность просеивания с увеличением количества ударов уменьшается. Это следует из того факта, что угол падения частицы на поверхности грохота от удара к удару увеличивается. Увеличивается также и угол отражения частиц, что свидетельствует о постепенном переходе режима с многократными ударами в режим скольжения по поверхности грохота. При малых углах наклона плоскости φ величина скоростей падения и отражения убывает от удара к удару, а при больших - возрастает. При этом дальность полета частицы вдоль плоскости убывает независимо от угла ее наклона. Один из вариантов расчета является особым случаем движения частицы – вариант, соответствующий углу наклона плоскости φ=5о . Последовательный ряд значений углов падения в табл. 1 не приведен полностью, однако расчеты показывают, что α0=5о; α1=4,6о ; α2=3,9о ; α3=2,3о ,т.е. эти значения убывают. Таким образом, если размер частицы меньше размера ячейки решетки грохота и при первых ударах частица не прошла сквозь решетку грохота, то при следующих ударах это все равно произойдет. Для величины коэффициента трения при ударе f=0,09, при котором производился данный расчет, это значение угла соответствует значению угла трения (tg5о=0,087).
Движения частицы относительно неподвижной поверхности грохота отличаются от движения частицы при его вибрации. Поэтому уравнения (2) - (6), описывающие процесс удара, следует привести к виду, соответствующему относительному движению частицы. Для моделирования движения частицы относительно вибрирующего грохота на этапе свободного полета необходимо учесть переносные силы инерции, содержащие ускорения поверхности грохота.
Опишем движение вибрирующей поверхности грохота двумя координатами 
, считая это движение поступательным. Тогда проекции скорости 
, а ускорение 
Поэтому проекция на нормаль относительной скорости частицы перед ударом выглядит следующим образом: 
а после 
, причем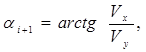
Соответственно, коэффициент восстановления после удара определится через составляющие относительной скорости:
. (14)
Направление силы трения зависит от направления относительной скорости частицы. Поэтому, если 
то сила трения направлена против оси X, а уравнения (4) остаются с теми же знаками. Если 
то трения нет вообще. Если 
то трение – в направлении оси X, т.е. в уравнении (4), куда оно входит, поменяется знак.
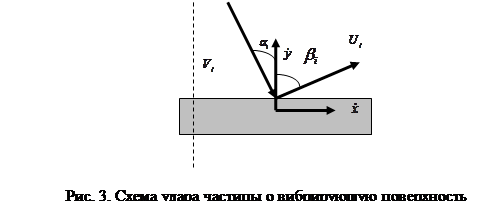
Обозначая угол наклона поверхности через 
, запишем дифференциальные уравнения относительного движения частицы в проекциях на оси X и Y, показанные на рисунке 1.
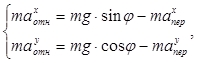. (15)
отсюда получим
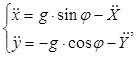. (16)
Таким образом, исследование движения рудной частицы сводится к численному моделированию многократного чередования ударов этапов их свободного полета с учетом переносного движения поверхности грохота.
Рецензенты:
Герц Эдуард Федорович, доктор технических наук, профессор, декан лесоинженерного факультета ФГБОУ ВПО «Уральский государственный лесотехнический университет», г. Екатеринбург.
Неволин Дмитрий Германович, доктор технических наук, профессор, заведующий кафедрой «Проектирование и эксплуатация автомобилей» ФГБОУ ВПО «Уральский государственный университет путей сообщения», г. Екатеринбург.
Библиографическая ссылка
Волков Е.Б., Ляпцев С.А. ВЛИЯНИЕ УГЛА НАКЛОНА РАБОЧЕЙ ПОВЕРХНОСТИ ВИБРАЦИОННОГО ГРОХОТА НА ЭФФЕКТИВНОСТЬ ГРОХОЧЕНИЯ // Современные проблемы науки и образования. – 2013. – № 4. ;URL: https://science-education.ru/ru/article/view?id=9642 (дата обращения: 19.04.2024).