Введение
Актуальность исследования методов помехоустойчивой обработки цифровых сигналов систем спутниковой связи (ССС) и сигналов вторичных сетей связи для модемов телефонного канала обусловлена необходимостью снижения вероятности ошибки в условиях приема, а также разделения сигналов с совмещением спектров. В работах [10, 11] предлагается использовать избыточность кадровых проверочных последовательностей и локализацию участков кадров для повышения качества приема, при невозможности переспроса искаженного сообщения.
При разработке новых алгоритмов и способов повышения качества приема сигналов возникает резонный вопрос, на какую величину улучшились параметры приема, т.е. имеет ли смысл использовать дополнительную обработку принятого сигнала. В данной работе предлагается оценить такой параметр, как вероятность ошибочного приема кодового слова (КС). Данный параметр будем оценивать для трех случаев – при передаче КС, кодированного помехоустойчивым кодом; при разбиении того же КС на блоки, кодированные канальным кодом и при локализации участков блоков КС, кодированных канальным кодом.
Оценка вероятности ошибочного приема КС для этих случаев поможет ответить на вопрос целесообразности использования способов дополнительной обработки для повышения качества приема сигналов.
Цель статьи заключается в разработке методики оценки вероятностей правильного приема, обнаружения ошибки и ошибочного приема кодового слова для случаев передачи исходного кодового слова, разбиения исходного КС на блоки, с учетом локализации участков блоков кода.
Методика оценки вероятностных характеристик приема кодового слова
На практике широко используется для анализа свойств кодов, исправляющих ошибки, [2] описание канала связи в виде двоичного симметричного канала (ДСК) без памяти. Для такого канала условная вероятность единичного символа, составляющего КС, при передаче в канале связи обычно задается представлением, изображенным на рисунке 1.
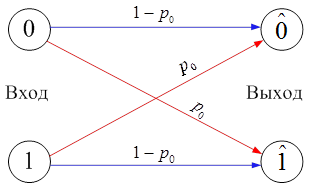
Рисунок 1. Граф переходов, задающий ДСК без памяти
В общем случае вероятность появления, по крайней мере, одной ошибки в КС определяется отношением (1)
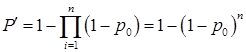 . (1)
. (1)
которое характеризует появление хотя бы одного из событий (ошибки КС), независимых в совокупности [4].
В выражении (1) n – число символов в КС; p0 – вероятность искажения 1-го символа в двоичном симметричном канале без памяти (см. рис. 1).
Вероятность того, что КС будет содержать e ошибок, задается отношением, определяющим вероятность совмещения всех событий, т.е.
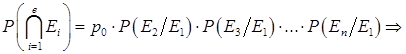
![]() (2)
(2)
где ![]() – задает событие искажения i-го символа в принимаемом КС;
– задает событие искажения i-го символа в принимаемом КС; ![]() – определяет число сочетаний из n по e и задается известным биномиальным коэффициентом [5]
– определяет число сочетаний из n по e и задается известным биномиальным коэффициентом [5]
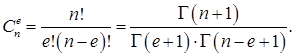 (3)
(3)
Здесь ![]() – гамма функция [6].
– гамма функция [6].
С учетом приведенных представлений, зададим следующие общие характеристики принимаемого (n, k) КС:
1) PПП – вероятность правильного приема КС:
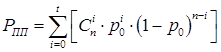 , (4)
, (4)
2) PОБ – вероятность обнаружения ошибки в КС:
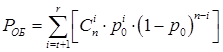 , (5)
, (5)
3) PОП – вероятность ошибочного приема КС:
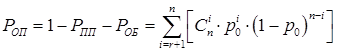 , (6)
, (6)
В данном случае t и r количественно характеризуют корректирующую и обнаруживающую способность исходного (n, k) кода и задаются соответствующими отношениями
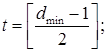
![]() (7)
(7)
где ![]()
![]() определяет минимальное расстояние по Хеммингу между всеми допустимыми кодовыми комбинациями исходно-заданного (n, k) кода;
определяет минимальное расстояние по Хеммингу между всеми допустимыми кодовыми комбинациями исходно-заданного (n, k) кода; ![]() – оператор, выделяющий целую часть.
– оператор, выделяющий целую часть.
Оценка ![]() для произвольного (n, k) кода, согласно [8], определяется из границ Плоткина и Хемминга:
для произвольного (n, k) кода, согласно [8], определяется из границ Плоткина и Хемминга:
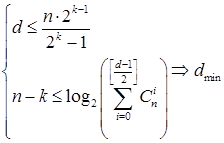 . (8)
. (8)
По существу решение (8) сводится к нахождению экстремума целевой функции
![]() , (9)
, (9)
с учетом ограничений, определяющих указанные ранее границы:
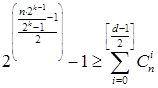 , (10)
, (10)
и ограничения на целочисленность переменной ![]() , определяемые согласно [7], в виде простых тригонометрических функций:
, определяемые согласно [7], в виде простых тригонометрических функций:
![]() , (11)
, (11)
Решение условной оптимизационной задачи (9) с учетом ограничений (10), (11) предлагается выполнить численно, с использованием метода множителей Лагранжа [9], при этом полином Лагранжа запишется в виде:
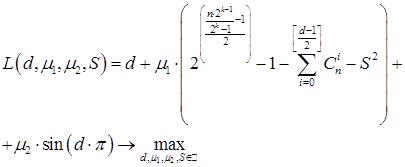 , (12)
, (12)
Нахождение экстремума (12) выполнено численно градиентным методом с переменной метрикой Дэвидона – Флэтчера – Пауэлла, стратегия которого подробно представлена в [3]. Определение вектора градиентов целевой функции (12) осуществляется численно методом Ньютона [1].
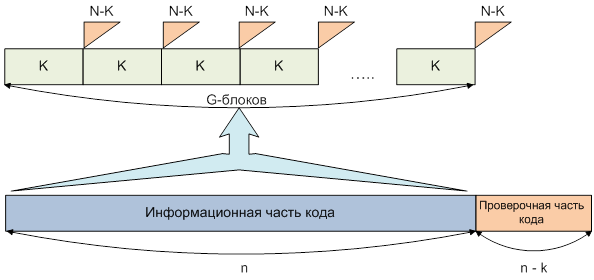
Рисунок 2. Разбиение информационной части кода на блоки
В случае предлагаемого разбиения информационной части КС на G блоков (рис. 2), причем каждый m-й блок ![]() представляет собой совокупность Km информационных частей (Nm, Km) кодовых слов, вероятность приема m-го блока КС будет определяться следующими характеристиками:
представляет собой совокупность Km информационных частей (Nm, Km) кодовых слов, вероятность приема m-го блока КС будет определяться следующими характеристиками:
1. ![]() – вероятность правильного приема m-го блока;
– вероятность правильного приема m-го блока;
2. ![]() – вероятность обнаружения ошибки в m-м блоке КС;
– вероятность обнаружения ошибки в m-м блоке КС;
3. ![]() – вероятность ошибочного приема m-го блока.
– вероятность ошибочного приема m-го блока.
Здесь ![]() и
и ![]() задают исправляющую и обнаруживающую характеристику (Nm, Km) кодовых слов, характеризующих m-й блок информационной части (n, k) КС, величина которых определяется по представленной выше методике.
задают исправляющую и обнаруживающую характеристику (Nm, Km) кодовых слов, характеризующих m-й блок информационной части (n, k) КС, величина которых определяется по представленной выше методике.
С учетом заданных представлений, вероятность ошибочного приема КС в случае разбиения информационной части на G блоков будет определяться отношением
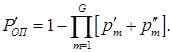 , (13)
, (13)
При условии того, что мы однозначно можем определить некоторое количество, например lm, символов в m-х блоках КС, приводящее к изменению исправляющей и обнаруживающей характеристик (Nm,Km) кодовых слов (![]() и
и ![]() ), заданные представления вероятностей для m-х блоков примут следующий вид:
), заданные представления вероятностей для m-х блоков примут следующий вид:
1. ![]() – вероятность правильного приема m-го блока;
– вероятность правильного приема m-го блока;
2. ![]() – вероятность обнаружения ошибки в m-м блоке КС;
– вероятность обнаружения ошибки в m-м блоке КС;
3. ![]() – вероятность ошибочного приема m-го блока.
– вероятность ошибочного приема m-го блока.
Последнее, по существу, приводит к снижению вероятности ошибочного приема КС, значение которой с учетом заданных представлений примет вид:
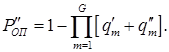 , (14)
, (14)
Для оценки полученных результатов проведена их экспериментальная проверка. В качестве исходного задан код (160, 144), применяемый для кодирования данных в системах Bluetooth. На передающей стороне КС, кодированное указанным кодом, разбивается на блоки и кодируется укороченным кодом Хэмминга (15, 10). Экспериментальная оценка вероятности ошибочного приема КС в соответствии с заданными представлениями выполнена для трех случаев:
– после кодирования КС кодом (160, 144);
– после кодирования КС кодом (160, 144) и разбиения на блоки КС кодированные кодом (15, 10);
– тоже, что в предыдущем пункте, но с учетом различного количества известных символов ![]() в блоке КС.
в блоке КС.

Рисунок 3. Вероятность ошибочного приема КС
Исследования выполнено с помощью системы математического моделирования MathCad 14. В ходе экспериментальной оценки получен график, отображающий вероятности ошибочного приема КС для трех указанных случаев (рис. 3).
Заключение
Из полученных результатов следует, что использование разбиения на блоки и локализация участков существенно уменьшают вероятность ошибочного приема КС. Увеличение длины локализованного участка в блоке также ведет к уменьшению вероятности ошибочного приема КС.
Таким образом, использование дополнительных способов обработки и локализации участков КС целесообразно использовать для повышения качества приема сигналов. Результаты математического моделирования продемонстрировали количественные параметры снижения вероятности ошибки в условиях приема при разбиении на блоки КС и локализации участков.
Рецензенты:
Архипов Н. С., д.т.н., доцент, сотрудник Академии ФСО России, г. Орел.
Иванов Б. Р., д.т.н., профессор, сотрудник Академии ФСО России, г. Орел.
Библиографическая ссылка
Шкердин А.Н., Полянский И.С. МЕТОДИКА ОЦЕНКИ ВЕРОЯТНОСТИ ОШИБОЧНОГО ПРИЕМА КОДОВОГО СЛОВА С УЧЕТОМ РАЗБИЕНИЯ НА БЛОКИ И ЛОКАЛИЗАЦИИ УЧАСТКОВ // Современные проблемы науки и образования. – 2013. – № 4. ;URL: https://science-education.ru/ru/article/view?id=9789 (дата обращения: 19.04.2024).



