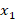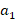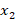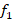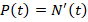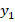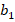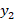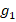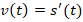Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Понятия изоморфизма и гомоморфизма возникли в теории групп в 1920-х гг. и являются одними из основных концептов современной математики. В силу своей универсальности данные понятия вышли за рамки математической науки и приобрели общенаучное значение. Они используются в химии, психологии, философии, литературе, лингвистике, педагогике. Использование изоморфизмов и гомоморфизмов является важным инструментом научного исследования и имеет существенное значение для понимания структуры и сущности самых разнообразных систем.

С методической точки зрения, важной отличительной чертой изо- и гомоморфизма является то, что они присущи не только системам, но и отдельным объектам, понятиям, утверждениям, теориям. Для педагога данная особенность открывает широкое поле возможностей. Принципы изоморфизма и гомоморфизма обеспечивают возможность решения множества биологических, химических, физических и других задач посредством построения изоморфных и гомоморфных математических моделей. При этом один и тот же изоморфный (гомоморфный) образ (в частности, математическая формула) может использоваться при решении не одной конкретной задачи, а множества задач схожей структуры, что приобретает особую актуальность при изучении математики студентами различных специальностей. Рассматривая реальный физический, химический, биологический процесс (в соответствии со специальностью студентов), преподаватель строит его изоморфный образ в виде аналитического математического выражения. Дальнейшее исследование изучаемого процесса осуществляется на изоморфной модели, а полученные результаты интерпретируются в соответствии с исходными данными. Такой подход позволяет продемонстрировать студентам возможности математического инструментария для решения различных «нематематических» задач, тем самым повысить их мотивацию к изучению такой сложной дисциплины, как высшая математика.

Цель исследования: рассмотреть возможности использования принципов изоморфизма и гомоморфизма в образовательном процессе при изучении высшей математики.

Материалы и методы исследования. В соответствии с поставленной целью был осуществлен анализ исследовательских работ, посвященных изоморфизмам и гомоморфизмам законов и моделей в различных областях науки (В.С. Кулабухов [1], Ю.А.Гастев [2], М.И Каргаполов [3], А.Г. Курош [4], О.А. Мелихова [5] и др.). Кроме того, были проанализированы научные труды, в которых изоморфизм и гомоморфизм рассматривались как инструмент педагогической деятельности (Л.Е. Осипенко [6], Л.Н.Горина [7], В.А. Макаридина [8], В.Е. Фирстов [9], Е.Н. Землянская [10], К.А. Кирсанов [11], А.В. Кащеева [12]). Организация образовательного процесса осуществлялась с учетом компетентностного и практико-ориентированного подходов, а также методики преподавания математики. Использовались такие методы педагогического исследования, как изучение и анализ литературы, опытная педагогическая работа, анкетирование, беседа, наблюдение, систематизация данных.

Изоморфизм (греч. isos – «одинаковый», morphe – «форма») – взаимно-однозначное соответствие между системами (т.е. каждому элементу первой системы 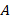соответствует единственный элемент второй системы 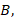и наоборот), сохраняющее структуру связей между элементами.

Если система 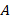изоморфна системе 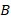, то система 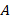может рассматриваться как модель системы 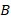. В этом случае изучение свойств модели дает информацию о свойствах реальной моделируемой системы. При изоморфизме степень соответствия модели и реальной моделируемой системы очень высока, что в значительной степени облегчает решение сложных задач в различных областях знаний.

Гомоморфизм (греч. homos – «одинаковый», morphe – «форма») – соответствие между системами, сохраняющее все значимые отношения, при котором каждому элементу первой системы 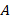соответствует ровно один элемент второй системы .

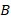В отличие от изоморфизма, гомоморфизм не является взаимно-однозначным соответствием. В данном случае степень соответствия между системами ниже – система 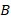не передает всех особенностей системы 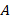, а является ее упрощенной моделью.

Главная методологическая функция, которую выполняет гомоморфизм, согласно Ю.А. Гастеву, «состоит в том, чтобы “свернуть” всю доступную нам информацию об исследуемых объектах, явлениях, процессах в гораздо более удобообозримую и удобообрабатываемую форму» [3, с. 33]. Происходящее в данном случае упрощение реальной исследуемой системы позволяет создать ее адекватную модель.

Результаты исследования и их обсуждение

Рассмотрим некоторую биологическую задачу 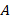, элементы 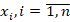которой связаны функциональным соотношением 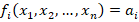, где 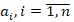– величины, определяемые условием задачи .

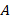Аналогично рассмотрим математическую задачу 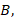элементы 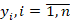которой связаны между собой соотношением 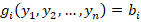, где 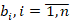– величины, заданные условием задачи .

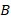Если существует взаимно-однозначное соответствие между задачами 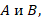при котором сохраняются функциональные соотношения между элементами рассматриваемых задач, то задачи изоморфны. В данном случае задачи 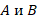тождественны с алгебраической точки зрения, то есть решаются по одному и тому же алгоритму. Решение задачи 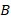будет являться решением задачи 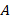, несмотря на то, что они относятся к различным областям знаний и сформулированы на различных языках (биологическом и математическом).

Рассмотрим две задачи:

1. Определить производительность жизнедеятельности популяции 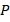(особей/с) в момент времени 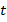, если количество бактерий 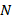с течением времени изменяется по закону .

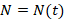2. Найти скорость движения материальной точки 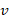(м/с) в момент времени 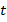, если она движется по прямой и с течением времени 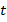ее положение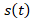меняется по закону .

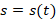Параметры обеих задач и функциональные соотношения, которыми они связаны, представлены в таблице.

Параметры и функциональные отношения задач

В обеих задачах присутствует общий элемент – время 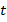, а функциональные соотношения одинаковы по структуре. Так как время – величина положительная, то 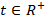(множество действительных положительных чисел) в обеих задачах. Размер популяции 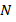и путь 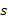также принадлежат множеству .

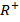Положив равенство элементов в обеих задачах (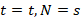), получим взаимно-однозначное соответствие 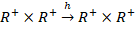, сохраняющее соотношение между элементами: 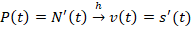. Тогда по определению изоморфизма математическая задача 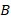является изоморфным образом биологической задачи .

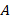Использование изоморфизмов позволяет не искать каждый раз новое решение для различных в содержательном плане задач (но одинаковых по структуре), а использовать одну и ту же математическую модель.

Рассмотрим, как работает принцип изоморфизма при решении конкретной задачи.

В реакции омыления этилового эфира уксусной кислоты едким натром при 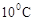концентрации эфира и щелочи равны соответственно 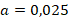моль/л и 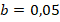моль/л. Определить время, необходимое для омыления 50% эфира, если константа скорости омыления .

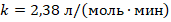Решение задачи осуществляется в три этапа.

I этап. Анализируется условие задачи и устанавливаются функциональные соотношения между параметрами (элементами) задачи. Осуществляется построение изоморфного образа, то есть перевод условия на формальный язык математики. Данный этап направлен на развитие у студентов мыслительных операций (анализ, синтез, обобщение, конкретизация, аналогия) как основы продуктивного мышления и познавательной деятельности.

Скорость реакции омыления согласно закону действующих масс определяется уравнением:

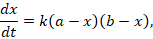
где x– количество моль/л вещества, прореагировавших за время tот начала реакции (для обоих веществ одинаково);

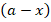– действующая концентрация уксусноэтилового эфира, моль/л;

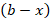– действующая концентрация гидроксида натрия, моль/л.

Представленное уравнение химии имеет математический изоморфный образ, который представляет собой дифференциальное уравнение с разделяющимися переменными.

Таким образом, исходная химическая задача сводится к задаче математической.

II этап. Осуществляется работа с моделью, то есть непосредственное решение изоморфной математической задачи. На данном этапе реализуется закрепление математических знаний и умений: решение дифференциальных уравнений с разделяющимися переменными, общее и частное решение.

Разделив переменные и проинтегрировав обе части дифференциального уравнения, получим его общее решение.

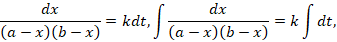
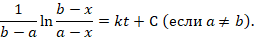
В начальный момент времен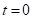и и 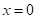. Подставив начальные данные в общее решение, найдем константу C: .

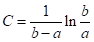Таким образом, частное решение исходного дифференциального уравнения относительно 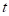имеет вид:

, .

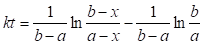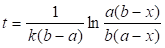III этап. Осуществляются переход в исходной задаче и интерпретация результата.

Найдем количество прореагировавших моль вещества к моменту омыления 50% уксусноэтилового эфира: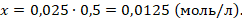

Определим время, необходимое для омыления 50% эфира: t = 6,8 мин.

Сделаем вывод: через 6,8 минут произойдет омыление половины уксусноэтилового эфира.

Таким образом, химическая задача решена посредством нахождения частного решения дифференциального уравнения, представляющего собой изоморфный образ скорости омыления этилового эфира уксусной кислоты едким натром.

Анализ научно-исследовательских работ (В.А. Макаридина [8], В.Е. Фирстов [9], Е.А. Швед [13], Г.И. Саранцев [14], Е.А. Молчанова [15], А.Г. Гейн, В.П. Некрасов [16] и др.) а также педагогического опыта позволяет сделать вывод о том, что, с практической точки зрения, принципы изоморфизма и гомоморфизма в образовательном процессе дают преподавателю следующие возможности.

1. Сгенерировать большое количество вариантов заданий профессионально-ориентированного характера (для контрольной или самостоятельной работы, типового расчета по вариантам и т.д.) на основе одной математической модели (изучаемой формулы, закона, теоремы). Обычно такие задания шаблонны, так как создание «оригинальных» задач занимает много времени. Но принципы изоморфизма и гомоморфизма позволяют преподавателю значительно сократить время на подготовку заданий, ориентированных на специализацию студентов, не меняя при этом прообраз в виде конкретных, изучаемых в данный момент теоремы, уравнения, метода решения.

2. Сделать процесс обучения профессионально ориентированным, при этом охватить студентов различных направлений подготовки, так как, выбрав изоморфный образ (конкретная формула или теорема, которую необходимо изучить), преподаватель может создать прообраз в виде задач из различных областей знаний с учетом специализации студентов, проводить аналогии между различными областями знаний: математикой и биологией, физикой, географией, химией, а также спецдисциплинами.

3. Сформировать у студентов понимание значимости математики, продемонстрировав, что любая, даже, на первый взгляд, нематематическая задача может быть представлена в виде математической модели и решена посредством аппарата математики. При этом опора на принципы изоморфизма и гомоморфизма позволяет построить идеальный, с точки зрения изучаемых параметров, аналог рассматриваемой системы, процесса, задачи, что обеспечивает достоверность получаемого результата.

4. Сформировать у студентов навыки использования приобретаемых математических знаний для решения реальных проблем профессиональной направленности посредством создания адекватных изоморфных математических моделей.

Анализ опыта использования принципов изоморфизма и гомоморфизма в образовательном процессе по математике позволил выделить некоторые особенности.

1. Один реальный объект (проблема, понятие, процесс) может иметь несколько изоморфных (гомоморфных) образов, рассмотрение каждого из которых будет давать одинаковый результат. И наоборот, один изоморфный (гомоморфный) образ может соответствовать нескольким реальным объектам.

2. Математические методы применяются не к реальной проблеме, а к ее изоморфной (гомоморфной) модели.

3. Если для сложного реального объекта затруднительно найти изоморфный или гомоморфный математический образ, то его можно представить в виде совокупности простых подсистем, для каждой из которых строится изоморфизм или гомоморфизм.

4. Изоморфная (гомоморфная) модель обладает свойством полноты, то есть ее исследование должно обеспечивать получение необходимой достоверной информации о реальном объекте.

Апробация применения принципов изоморфизма и гомоморфизма в образовательном процессе по математике осуществлялась на базе факультета электроники Рязанского государственного радиотехнического университета (по направлениям подготовки: «Электроника и наноэлектроника», «Химическая технология»). Дисциплина «Математика» преподается 6 часов в неделю. Несмотря на то что математика является профильной дисциплиной, у студентов отмечается низкий уровень мотивации к ее изучению. В рамках проводимого исследования был создан комплекс задач по различным темам курса, которые использовались в образовательном процессе как для аудиторной, так и для самостоятельной работы. Построение задач осуществлялось в соответствии с принципами изоморфизма и гомоморфизма, что позволило: во-первых, создать большое количество задач профессиональной направленности (электротехника, химия), изоморфным прообразом которых являлись конкретные математические формулы, уравнения и пр.; во-вторых, обеспечить заинтересованность студентов в изучении математики за счет рассмотрения интересных для них задач, имеющих непосредственное отношение к их будущей профессии. Беседа со студентами и их анкетирование, анализ результатов сессии позволили сделать вывод о том, что применение принципов изоморфизма и гомоморфизма повышает уровень мотивации учащихся, они видят область применения изучаемого математического материала при решении конкретных задач практики.

Выводы. Построение математических моделей реальных процессов (химических, биологических, физических и др.), описание изучаемых явлений посредством математических моделей (закономерностей, уравнений, неравенств, систем) возможны благодаря использованию изоморфизмов и гомоморфизмов. Решение сложной проблемы сводится к нахождению изоморфного (или гомоморфного) образа, представленного математическими символами.

В образовательном процессе использование принципов изоморфизма и гомоморфизма позволяет: 1) провести аналогию между математикой и другими научными областями знаний, которые имеют значение для студентов; 2) создать профессиональную ориентацию образовательного процесса по математике; 3) преподавателю создать банк «оригинальных», ориентированных на специализацию студентов, задач; 4) продемонстрировать значимость математики, ее место в системе наук.