«Векторы и координаты в пространстве» – одна из содержательных линий школьного курса «Геометрии». В соответствии с примерной рабочей программой по математике («Геометрия», базовый уровень) для средней общеобразовательной школы обучающиеся в 10 классе должны уметь решать задачи на применение векторно-координатного метода; применять известные аналитические методы при решении стандартных математических задач на вычисление расстояний между двумя точками, от точки до прямой, от точки до плоскости, между скрещивающимися прямыми. В 11 классе: исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин [1].
В соответствии с примерной рабочей программой по математике (углубленный уровень) обучающиеся должны: свободно оперировать понятием «вектор в пространстве»; выполнять операции над векторами; задавать плоскость уравнением в декартовой системе координат; решать геометрические задачи на применение векторно-координатного метода [2]. Таким образом, элементы аналитической геометрии дополняют курс школьной геометрии как на базовом, так и на углубленном уровнях ее изучения.
Для аналитической геометрии определяющим является не предмет, а метод, заключающийся в том, что геометрическим объектам сопоставляются некоторым стандартным способом соответствующие алгебраические уравнения или их системы. Для того чтобы обучающиеся научились изучать свойства геометрических объектов, используя законы алгебры, необходимо поэтапное формирование соответствующего понятийного аппарата, с помощью которого они научатся отождествлять геометрические объекты с точками на плоскости и в пространстве, выводить уравнения линий и поверхностей, выражающие зависимости между координатами точек.
Элементы аналитической геометрии в школьном курсе начинают изучаться в 5 классе с понятия координатного луча, позволяющего определить положение точки вдоль прямой и представляющего собой луч, на котором задано начало отсчёта, направление отсчёта и единичный отрезок. Далее вводится понятие координатной прямой, при этом координаты рассматриваются как числовой эквивалент первичного геометрического понятия – точки. В 6 классе вводятся понятия «координатная ось» и «система координат» [3].
 |
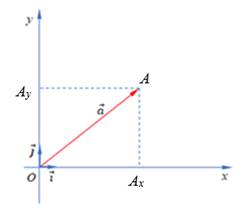Изучение самого метода координат средствами алгебры происходит в 9 классе [4, с. 222-226; 5, с. 140] с определения координат вектора на плоскости через его разложение по двум упорядоченным неколлинеарным векторам
: 
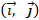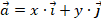, где x и y – это координаты вектора относительно 
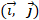(рис. 1).
Рис. 1. Проекции вектора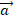 
на оси координат
Здесь устанавливается соответствие между геометрическими объектами – точками плоскости и алгебраическими объектами – упорядоченными парами действительных чисел. Однако опускаются некоторые важные теоретические моменты, отражающие сущность координатного метода, который заключается в задании системы координат. Система координат на плоскости состоит, как показано на рисунке 1, из двух взаимно перпендикулярных ориентированных прямых (осей координат Ox и Oy) и эталона длины (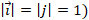
. Координаты точки A на плоскости xOy определяются как соответствующие проекции OAx и OAy точки A на оси Ox и Oy. Поскольку после задания системы координат каждую точку прямой можно охарактеризовать ее координатами, то систему координат можно рассматривать на каждой из осей, что естественным образом позволяет свести определение координат от двумерного случая к одномерному. Задание системы координат, в частности, на прямой состоит из трех элементов:
1) положительное направление (одно из двух возможных);
2) эталон длины;
3) определенно выбранная на прямой точка – начало координат.
Поэтому, прежде чем сразу рассматривать определение координат вектора на плоскости, как это предлагается в школьных учебниках [4, с. 222-226; 5, с. 140], на наш взгляд, необходимо с надлежащей полнотой показать сущность координатного метода на прямой. Для этого необходимо сформировать у обучающихся понятия координатной оси с правоориентированным базисом на прямой, используя аксиомы отношения порядка, и вывести формулы определения координат вектора относительно заданного базиса без чертежа на основе теоремы Шаля для отрезков.
Цель исследования: составить методическую схему определения координат вектора с использованием теоремы Шаля для отрезков.
Материал и методы исследования
Начнем с аналитической геометрии на прямой, рассмотрим введение понятия ориентированной прямой или оси. Понятие ориентированной прямой связано с понятием базисного вектора. На рисунке 2 показана прямая l с заданным на ней направлением (произвольным вектором)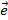 
. В этом случае говорят, что на прямой задан базисный вектор 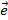, который и определяет направление на этой прямой, а длина этого вектора соответствует масштабному отрезку.
Рис. 2. Ориентированная прямая (ось) с заданными на ней точками A, B
Таким образом, направление прямой l определяет базисный вектор 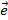, тогда такая прямая будет называться ориентированной. Задавая базис на прямой, мы получаем – ось.
Если базис 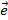определяет ориентацию прямой l, то он называется положительно ориентированным по отношению к данной ориентации прямой. Подойдем к определению координатной оси с правоориентированным базисом. Для этого можно ввести понятие отношение порядка или отношения предшествования и показать, что на любой прямой существуют два взаимно противоположных отношения предшествования [6, с. 22], каждое из которых определяется заданием на прямой некоторой ориентации.
На прямой l возьмем две точки A и B, и пусть, например, точка A предшествует точке B, тогда говорят, что на множестве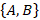 
задано отношение порядка или отношение предшествования, и множество 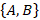будет представлять собой упорядоченное множество. Отношение порядка обозначают символом 
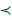, значит 
.
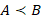Отношение называется отношением порядка, если оно обладает свойствами:
1) если 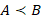, то 
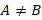– свойство антирефлексивности;
2) если 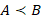и 
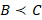, то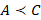 
– свойство транзитивности;
3) если 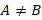, то либо 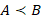, либо 
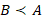– свойство полноты.
По заданному отношению порядка 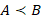можно построить новое отношение порядка 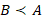, которое будет противоположным заданному. В качестве аксиомы принимается утверждение: на любой прямой существуют два взаимно противоположных отношения предшествования.
Таким образом, каждое из этих отношений предшествования определяется заданием на прямой некоторой ориентации, или каждое из отношений предшествования, предусмотренное данной аксиомой, называется ориентацией прямой.
После того как на прямой l задан масштабный отрезок 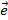измерения длины (длина которого принимается равной 1), можно рассматривать расстояние между точками A и B относительно выбранного направления, то есть введем понятие «относительного расстояния» между двумя точками. Возьмем на прямой l произвольную точку O – начало координат. Ось Ol, на которой фиксирована точка O, называется осью координат. Расстояние между точками не является абсолютной величиной, поэтому, если направление от A к B совпадает с направлением ориентированной прямой l, то относительное расстояние будет положительным +(AB) или отрицательным –(BA), если направление противоположно l.
Очевидно,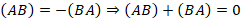 
.
Пусть на прямой l даны три точки A, B и C, тогда на основании свойства транзитивности для соответствующих отношений порядка можно записать: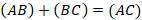 
или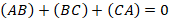 
(теорема Шаля).
Выберем на оси координат масштабный отрезок, его длина соответствует длине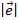 
базисного вектора и равна 1. Используя такой отрезок в качестве масштаба (эталона измерения), мы сможем численно определять расстояния между двумя любыми точками числовой прямой Ol.
Упорядоченная пара точек A и B (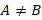), принадлежащих числовой оси Ol, определяет направленный отрезок 
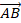. Первая точка A – начало 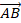, вторая точка B – конец 
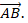Длиной 
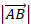или модулем направленного отрезка 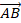называют длину ненаправленного отрезка 
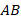, которая будет определяться проекцией 
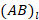вектора 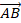на числовую ось Ol.
Если для трех точек A, B, C числовой прямой Ol заданы соответствующие отношения порядка ,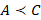 
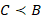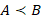, , тогда векторы 
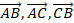– положительно ориентированные, так как их направления совпадают с направлением оси Ol. Согласно теореме Шаля для любых трех точек A, B, C числовой прямой Ol будет справедливо равенство:
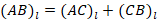, где (1)
, 
, 
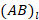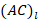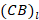– проекции векторов 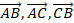на ось Ol соответственно. Для проекций векторов введем обозначения:
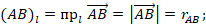
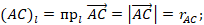
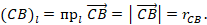
Проекции векторов 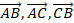на ось Ol равны их модулям соответственно. Так как 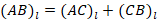, подставив с учетом обозначений, получим:
.
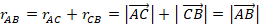Рассмотрим частный случай, когда точка A принадлежит отрезку [B, C] c заданным правоориентированным базисом (рис. 3).
Рис. 3. Ось координат с правоориентированным базисом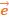 
Найдем проекцию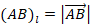 
вектора 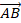на ось Ol. По теореме Шаля:
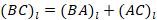. Так как 
,
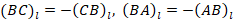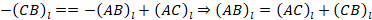, то есть для любых трех точек A, B и C, принадлежащих числовой оси Ol, выполняется равенство (1).
Каждой точке координатной оси можно поставить в соответствие число – координату (абсциссу) этой точки, равное расстоянию от неё до начала координат. Координата – (лат., приставка co – вместе, ordinatus – упорядоченный). Для этого достаточно установить:
1) базис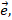 
определяющий ориентацию прямой l, то есть направление, называемое – положительным;
2) определенно выбранную на прямой l точку O – начало координат.
Любой точке на числовой оси можно указать симметричную ей точку, которая находится на таком же расстоянии от начала координат, что и первая. Поэтому на числовой оси необходимо выбрать одно из двух возможных направлений, которое считается положительным.
Для произвольной точки A, принадлежащей Ol, назовем координатой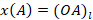 
или просто x – относительное расстояние от начала координат O до этой точки.
Теорема Шаля имеет фундаментальное значение и позволяет, не используя чертеж, рассуждать об относительных расстояниях между точками на ориентированной прямой [7, с. 7]. На основании теоремы Шаля выведем формулу, с помощью которой можно определить координаты направленного отрезка 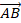на прямой, заданного двумя точкам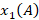и 
и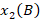 
прямой. Рассмотрим случай, когда всем точкам на числовой оси, расположенным от начала координат в положительном направлении (с заданным право ориентированным базисом), поставлены в соответствие их расстояния от начала координат. Введем обозначения:
;
.
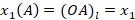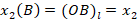На прямой координата 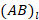направленного отрезка 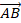, заданного двумя точкам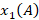и и 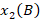, вычисляется по формуле:
.
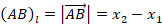Действительно, по теореме Шаля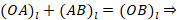 
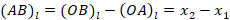. Таким образом, не делая чертеж, можно вывести формулу, позволяющую определить координаты направленного отрезка 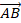, заданного двумя точками на координатной прямой.
Возвращаясь к рисунку 1 и сохраняя подход, предложенный в школьных учебниках геометрии, можно определить координату вектора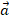 
на числовой оси относительно введенного базиса 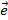. Пусть на прямой задан единичный вектор 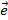, тогда для любого вектора 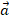, принадлежащего этой прямой, существует единственное действительное число x, такое, что 
,
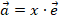где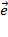 
– базисный вектор;
x – координата вектора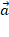 
относительно базиса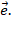 
Координата x вектора определяется однозначно, как отношение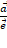 
, причем все ненулевые векторы, сонаправленные с вектором 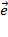, имеют положительные координаты, а противоположно направленные – отрицательные. Например, если вектор 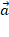представим в виде 
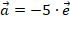, то его координата относительно базиса 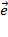равна –5. Координата нулевого вектора равна 0.
Если на плоскости задана упорядоченная пара неколлинеарных векторов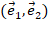 
– базис на плоскости (рис. 4), то для любого вектора 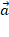, принадлежащего этой же плоскости, существует единственная упорядоченная пара чисел 
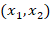, таких, что вектор 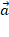представим в виде: 
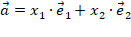. Действительно, как только на плоскости мы задаем базис, плоскость становится ориентированной. Базис 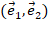называется правым, если при взгляде на плоскость виден кратчайший поворот от первого вектора 
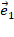ко второму вектору 
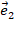, как идущий против часовой стрелки; левым – если виден поворот против часовой стрелки. При определении координат вектора на плоскости мы будем пользоваться правым базисом. Рассмотрим определение координат произвольного вектора на плоскости.
Зададим на плоскости правый базис 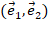, построим прямые 
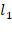и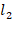 
:
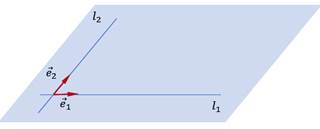
Рис. 4. Задание базиса на плоскости
Если на плоскости задана точка O и базис 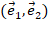, тогда говорят, что на плоскости задана система координат 
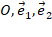, где точка O – начало координат. Если через точку O провести прямые в заданном направлении базисных векторов 
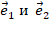, то получим на плоскости соответствущие оси координат 
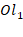и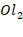 
. Если векторы 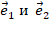взаимно перпендикулярны и их модули равны 1, то получим частный случай декартовой системы координат – прямоугольную систему координат на плоскости. Пусть вектор 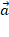принадлежит данной плоскости (рис. 5), требуется определить его координаты.
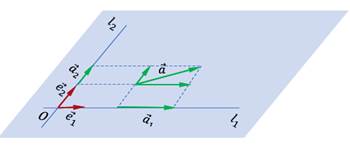
Рис. 5. Разложение вектора 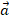по базису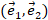 
Вектор 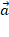можно представить в виде суммы двух векторов: 
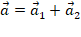, где векторы 
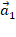и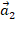 
относительно базиса 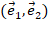представимы в виде:
; 
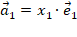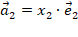соответственно, то есть вектор 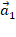можно разложить по базису 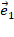прямой 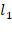, а вектор 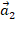– по базису 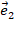прямой 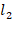. Таким образом, упорядоченная пара чисел (
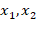) однозначно определяет на плоскости координаты заданного вектора 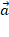относительно базиса .
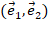Основные результаты
На основе вышеизложенного можно сформировать методическую схему для изучения «Координатного метода»:
1. Ввести понятия:
оси, как прямой, направление которой определяется направлением заданного на ней произвольного ненулевого вектора 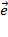, называемого базисом;
координатной оси с правоориентированным базисом. Для этого нужны понятия:
отношение порядка;
относительное расстояние между двумя точками;
ось координат;
правоориентированный вектор;
координаты вектора (через относительное расстояние от начала координат до заданной на координатной оси точки).
2. На основании теоремы Шаля для отрезков вывести формулу определения координаты вектора, заданного двумя точками на координатной оси.
3. Определить координату вектора 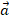на числовой оси относительно базиса .
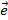4. Ввести понятие базиса на плоскости и рассмотреть определение координат произвольного вектора на плоскости относительно введенного базиса.
Заключение
Использование вышеизложенного материала в качестве введения элементов аналитической геометрии в школьный курс геометрии позволяет систематизировать ранее известные понятия, наглядно осуществить вывод формул, относящихся к простейшим задачам аналитической геометрии: определение расстояния между двумя точками; деление отрезка пополам; деление отрезка в данном отношении, и в дальнейшем переходить к изучению более сложных вопросов, касающихся различных преобразований плоскости (движение, сжатие, растяжение), классификация которых также осуществляется на основании теоремы Шаля.
Такой подход к изучению координатного метода обеспечивает связь между базовым курсом школьной программы и программой для классов с углубленной математической подготовкой и может быть полезен тем выпускникам школ, кто проявляет интерес к математике и естественным наукам.