Введение
Развитие и повышение производительности современных вычислительных систем неразрывно связано с параллелизмом вычислительного процесса. В различных областях вычислительной техники нашли применение такие аппаратные платформы, как многоядерные процессоры общего назначения, графические ускорители CUDA, а также вычислители на основе ПЛИС (FPGA и CPLD). Вычислители с параллельной архитектурой начинают все шире применяться и во встраиваемых системах для решения задач моделирования и управления в реальном масштабе времени [1].
Данный класс вычислительных систем предъявляет новые требования к математическому обеспечению, лежащему в основе вычислительных моделей. В первую очередь речь идет о методах численного интегрирования, пригодных для аппаратной реализации. Численное решение дифференциальных уравнений – одна из первых задач, для которых создавались цифровые вычислительные машины, однако классические методы численного интегрирования позволяют создать лишь рекуррентные вычислительные модели, которые неизбежно вычисляются последовательно. Ярким примером таких методов является широко известное семейство явных методов Рунге-Кутты, имеющих ряд положительных качеств: малое число действий, малое запаздывание сигнала, простота программной реализации. В то же время строгая рекуррентность вычислительных моделей, построенных с использованием методов Рунге-Кутты, существенно ограничивает их применение на аппаратных платформах с параллельной архитектурой.
Известны также параллельные реализации неявных методов Рунге-Кутты [4]. Однако по сравнению явными методами они имеют гораздо большую вычислительную сложность, которая быстро нарастает при увеличении порядка моделируемой системы, а также высокую трудоемкость самой процедуры распараллеливания. В настоящей работе предлагается семейство явных численных методов интегрирования на основе метода последовательного интегрирования, впервые сформулированного в работе [2] и далее получившего развитие в работах [1, 3]. Метод предполагает распараллеливание вычислительного процесса за счет создания нескольких независимых вычислительных процессоров, комбинация решений которых дает математическое описание динамической системы с заданной точностью.
Аппаратно-ориентированный численный метод второго порядка точности
Из работ [1, 3, 4] известен численный метод, называемый методом последовательного интегрирования (МПИ). Метод имеет второй порядок алгебраической точности.
Рассмотрим систему дифференциальных уравнений второго порядка (1), записанную в нормальной форме Коши:
![]() (1)
(1)
Запись в виде матрицы пространства состояний той же системы имеет вид:
![]()
![]()
Здесь ![]() – вектор переменных состояния,
– вектор переменных состояния, ![]() и
и ![]() – матрицы коэффициентов,
– матрицы коэффициентов, ![]() – входной сигнал.
– входной сигнал.
Суть метода последовательного интегрирования второго порядка заключается в том, что правые части уравнений системы интегрируются с помощью модифицированного метода Эйлера на двух вычислительных процессорах параллельно и независимо друг от друга. Для уравнения (1) алгоритм вычислений в первом интегрирующего процессора может быть записан следующим образом:
![]()
![]()
![]()
![]() (2)
(2)
![]()
![]()
Здесь ![]() – обозначение значения переменной на шаге
– обозначение значения переменной на шаге ![]() ,
, ![]() – значение входного сигнала в момент времени
– значение входного сигнала в момент времени ![]() ,
, ![]() – шаг численного интегрирования.
– шаг численного интегрирования.
Коэффициенты с символом * корректируются до ![]() исходя из сравнения выражения на одном шаге с разложением решения в ряд Тейлора, причем делается это лишь в одном вычислительном процессоре. Во втором интегрирующем процессоре вычислительный процесс идет в «обратном» направлении, то есть те действия, которые в первом процессоре выполняются последними, на втором процессоре выполняются первыми. Полученные на первом и втором процессоре значения переменных состояния усредняются по формуле
исходя из сравнения выражения на одном шаге с разложением решения в ряд Тейлора, причем делается это лишь в одном вычислительном процессоре. Во втором интегрирующем процессоре вычислительный процесс идет в «обратном» направлении, то есть те действия, которые в первом процессоре выполняются последними, на втором процессоре выполняются первыми. Полученные на первом и втором процессоре значения переменных состояния усредняются по формуле
![]()
где ![]() – значение вычисленной на i- том процессоре i-той перемененной состояния на шаге
– значение вычисленной на i- том процессоре i-той перемененной состояния на шаге ![]() .
.
Для доказательства порядка метода рассмотрим разложение в ряд Тейлора для системы (1) в окрестностях точки ![]() . После некоторых несложных преобразований мы получим выражение для переменных состояния
. После некоторых несложных преобразований мы получим выражение для переменных состояния ![]() и
и ![]() (в точке
(в точке ![]() ). Это разложение совпадает с результатом, получаемым по методу Рунге-Кутты 2, с точностью до
). Это разложение совпадает с результатом, получаемым по методу Рунге-Кутты 2, с точностью до ![]() :
:
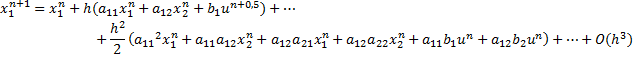
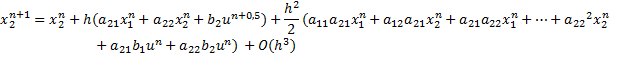
С помощью описанного выше метода мы также получаем подобный результат, за исключением наличия несущественных для метода 2 порядка членов, умножаемых на ![]() и
и ![]() , а также отсутствия существенных членов
, а также отсутствия существенных членов ![]() в выражении для
в выражении для ![]() и
и ![]() в выражении для
в выражении для ![]() :
:
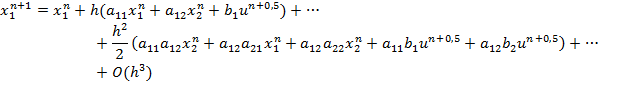
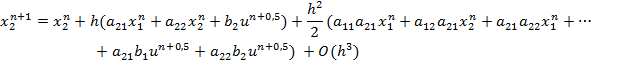
Отсутствие членов вида ![]() заставляет ввести их в выражения метода в виде дополнительной коррекции. В основополагающей работе [2] утверждается, что необходимо скорректировать лишь один процессор, однако представляется целесообразным опробовать на практике т.н. симметричную коррекцию с добавлением отсутствующих членов ряда в оба процессора. В качестве иллюстрации рассмотрим решение задачи Коши для автономной системы
заставляет ввести их в выражения метода в виде дополнительной коррекции. В основополагающей работе [2] утверждается, что необходимо скорректировать лишь один процессор, однако представляется целесообразным опробовать на практике т.н. симметричную коррекцию с добавлением отсутствующих членов ряда в оба процессора. В качестве иллюстрации рассмотрим решение задачи Коши для автономной системы ![]() при следующем значении матрицы
при следующем значении матрицы![]()
![]() (3)
(3)
и начальных условиях: ![]() ;
; ![]() . Время моделирования зададим равным 5 с. при шаге интегрирования 0.01 с. На рисунке 1 представлена относительная погрешность решения системы (3) методом последовательного интегрирования с традиционной асимметричной коррекцией и классическим последовательным методом Рунге-Кутты 2 порядка.
. Время моделирования зададим равным 5 с. при шаге интегрирования 0.01 с. На рисунке 1 представлена относительная погрешность решения системы (3) методом последовательного интегрирования с традиционной асимметричной коррекцией и классическим последовательным методом Рунге-Кутты 2 порядка.
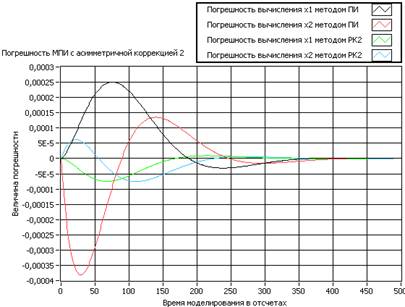
Можно заметить, что вариант метода ПИ с асимметричной коррекцией несколько уступает по точности методу РК2. Изменим коррекцию на симметричную вида ![]() и найдем погрешность решения системы (2) еще раз.
и найдем погрешность решения системы (2) еще раз.
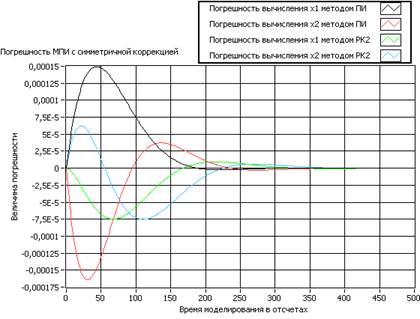
Как видно из рисунка 2, максимальная погрешность вычислений уменьшилась примерно в три раза, а для установившегося значения более чем в 10 раз: с асимметричной коррекцией установившееся значение переменной ![]() равно 4,07-7, а с симметричной – 2,60*10-8.
равно 4,07-7, а с симметричной – 2,60*10-8.
Оценка вычислительных затрат
Оценка числа действий для метода последовательного интегрирования показывает, что предлагаемая его модификация при решении системы (2) требует 15 последовательных операций умножения (по 14 в каждом процессоре плюс операция усреднения между процессорами) и восемь операций сложения. При моделировании линейных стационарных систем можно использовать прием предрасчета коэффициентов, умножив заранее коэффициенты системы на шаг интегрирования и внеся в них требуемую коррекцию. Тогда вычислительные затраты аппаратно-ориентированного метода составят 7 операций умножения и 7 сложения, итого 14 последовательных действий. Для сравнения рассмотрим алгоритм решения системы (2) по методу Рунге-Кутты 2 порядка (РК2):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Нетрудно убедиться, что для решения системы (2) методом РК2 требуется 18 операций умножения и 12 операций сложения; всего 30 последовательных действий. Помимо свойства параллелизма, алгоритм аппаратно-ориентированного метода удобен для реализации на вычислителях с представлением данных с фиксированной запятой, обеспечивая меньшую инструментальную погрешность и удобство масштабирования коэффициентов системы.
Несмотря на обозначенные преимущества и описанный в настоящей статье способ усовершенствованной симметричной коррекции решения, метод последовательного интегрирования имеет второй порядок алгебраической точности и не является абсолютно устойчивым, что нивелирует его преимущества, например, по сравнению с методом трапеций, обладающим абсолютной устойчивостью при том же порядке точности. Попробуем получить метод последовательного интегрирования более высокого порядка, применив экстраполятор Ричардсона [5]. Этот известный прием позволяет увеличить точность метода на один порядок за счет увеличения числа последовательно выполняемых арифметических действий вдвое. Применив экстраполятор Ричардсона к методу МПИ, мы получим систему из четырех решающих процессоров, первые два из которых будут аналогичны процессорам метода второго порядка, а третий и четвертый будут представлять собой их «двойные» аналоги с шагом интегрирования ![]() . Число действий удваивается из-за необходимости получить решение для 3-4го процессоров в тех же точках, что и 1-2го при меньшем шаге:
. Число действий удваивается из-за необходимости получить решение для 3-4го процессоров в тех же точках, что и 1-2го при меньшем шаге:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
где ![]() . Вычислительный процесс в четвертом процессоре будет организован сходным образом на основе выражений для второго процессора.
. Вычислительный процесс в четвертом процессоре будет организован сходным образом на основе выражений для второго процессора.
Известно, что значение погрешности численного метода второго порядка приблизительно равно ![]() , где
, где ![]() – некоторая величина, зависящая от вида решаемой системы. Обозначим точное значение решения как
– некоторая величина, зависящая от вида решаемой системы. Обозначим точное значение решения как ![]() , погрешность решения как
, погрешность решения как ![]() , а численное решение как
, а численное решение как ![]() . Для каждого из
. Для каждого из ![]() процессоров численное решение
процессоров численное решение ![]() равно:
равно:
![]()
Из свойств метода последовательного интегрирования следует, что ![]() , а
, а ![]() . При этом
. При этом ![]() ,
, ![]() , где
, где ![]() , т.е.
, т.е. ![]() , а
, а ![]() . Зная эти соотношения, выразим
. Зная эти соотношения, выразим ![]() через
через ![]() согласно правилу Ричардсона:
согласно правилу Ричардсона:
![]()
Проверим порядок точности полученного метода путем оценки погрешности решения той же системы (3) с теми же параметрами моделирования, что и ранее для метода второго порядка (![]() =5 c.,
=5 c., ![]() =0.01 c.). Для сравнения проведем моделирование также классическим методом Рунге-Кутты 3 порядка. Результаты моделирования приведены на рисунке 3.
=0.01 c.). Для сравнения проведем моделирование также классическим методом Рунге-Кутты 3 порядка. Результаты моделирования приведены на рисунке 3.
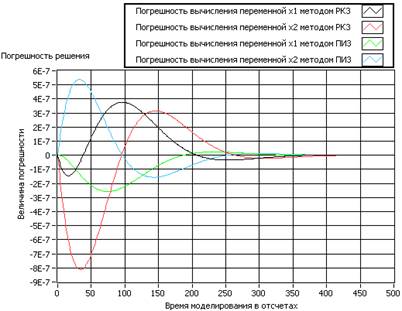
Повышение точности, достигаемое применением экстраполятора, казалось бы, не стоит увеличения вычислительных затрат в два раза, однако при детальном сравнении выражений, определяющих значения переменных состояния ![]() и
и ![]() в точке
в точке ![]() для решателя по методу ПИ3 с аналогичными выражениями для решателя по методу Рунге-Кутты четвертого порядка (РК4), можно заметить, что за исключением членов при
для решателя по методу ПИ3 с аналогичными выражениями для решателя по методу Рунге-Кутты четвертого порядка (РК4), можно заметить, что за исключением членов при ![]() и более старших степеней они различаются лишь отсутствием диагональных коэффициентов, помноженных на
и более старших степеней они различаются лишь отсутствием диагональных коэффициентов, помноженных на ![]() . К сожалению, объем этих выражений не позволяет привести их в данной статье. Добавим отсутствующие члены к уже имеющимся выражениям для коррекции диагональных коэффициентов, которые теперь примут вид:
. К сожалению, объем этих выражений не позволяет привести их в данной статье. Добавим отсутствующие члены к уже имеющимся выражениям для коррекции диагональных коэффициентов, которые теперь примут вид: ![]() и заново оценим погрешность решения системы (2) (рисунок 4):
и заново оценим погрешность решения системы (2) (рисунок 4):
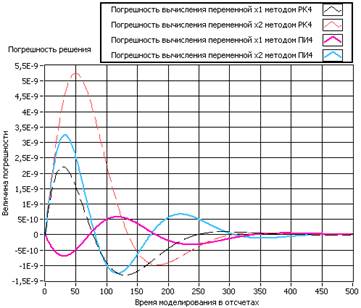
Таким образом, применение экстраполятора Ричардсона совместно с новой коррекцией диагональных коэффициентов дало прирост точности метода последовательного интегрирования не на один порядок, а на два. Оценим вычислительные затраты полученного метода четвертого порядка по сравнению с методом Рунге-Кутты 4, имеющим тот же порядок точности. Для повышения порядка метода мы удвоили число действий в процессорах, поэтому число последовательно выполняемых умножений при решении системы вида (1) возрастет до 33, а сложений до 17. Если система линейна и стационарна, то можно использовать прием предварительного расчета коэффициентов, и количество умножений и сложений уменьшится до 14 для каждого из типов операций. Для сравнения, решение системы (2) методом Рунге-Кутты 4 требует выполнения 38 умножений и 26 сложений, производимых строго последовательно. Кроме того, метод ПИ 4 порядка сохранил главное свойство всех методов последовательного интегрирования – приспособленность для аппаратной реализации, в том числе на платформах с представлением данных с фиксированной точкой, за счет сравнительно простой организации процедуры масштабирования коэффициентов модели [1].
Заключение
В работе предложен новый способ коррекции погрешности методов последовательного интегрирования, основанный на анализе разложения решения в ряд Тейлора. Также предложен способ повышения порядка точности МПИ за счет применения экстраполятора Ричардсона. Получены и экспериментально исследованы методы последовательного интегрирования третьего и четвертого порядка алгебраической точности. Оценки вычислительных затрат показывает преимущество предлагаемых методов при аппаратном моделировании динамических систем, описываемых обыкновенными дифференциальными уравнениями на платформах, предусматривающих параллелизм вычислительного процесса. Дальнейшими направлениями исследований будут являться оценка устойчивости полученных численных методов, модификация методов последовательного интегрирования для применения в решателях с переменным шагом интегрирования, адаптация МПИ для решения нелинейных систем дифференциальных уравнений и уравнений в частных производных. Полученные результаты можно эффективно использовать при проектировании встраиваемых систем управления и обработки сигналов, создании инструментальных пакетов моделирования и аппаратных ускорителей моделирования, а также при численном решении дифференциальных уравнений на ЭВМ с многоядерной архитектурой.
Работа выполнена в СПбГЭТУ при финансовой поддержке Российского фонда фундаментальных исследований в рамках договора № НК 14-01-31277\14 от 06.02.2014 г.
Рецензенты:
Авдеев Б.Я., д.т.н., профессор кафедры информационно-измерительных систем и технологий, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Пузанков Д.В., д.т.н., профессор кафедры вычислительной техники, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Бутусов Д.Н., Каримов А.И., Каримов Т.И., Долгушин Г.К. СЕМЕЙСТВО АППАРАТНО-ОРИЕНТИРОВАННЫХ МЕТОДОВ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ // Современные проблемы науки и образования. – 2014. – № 4. ;URL: https://science-education.ru/ru/article/view?id=13480 (дата обращения: 19.04.2024).



