Моделирование как метод научного познания основано на способности субъекта (человека) вычленять сходные признаки или свойства у различных предметов, явлений и устанавливать определенное соотношение между ними. При этом указанные признаки или свойства выступают в роли своеобразного основания, ориентира, знака, при воспроизведении которых формируется образ моделируемого объекта. Таким образом, признак, свойство или некая их совокупность являются своеобразным побудительным мотивом к последующим действиям, определяемым соответствующим контекстом. Иначе говоря, имеет место привлечение элементов семиотики при целенаправленном использовании метода научного познания.
Семиотика традиционно трактуется как наука, занимающаяся сравнительным изучением знаковых систем - от простейших систем сигнализации до естественных языков и формализованных языков науки [2]. Основными функциями знаковой системы являются:
- передача сообщения или выражение смысла.
- функция общения, т.е. обеспечение понимания слушателем или читателем передаваемого сообщения, а также побуждение к действию, эмоциональное воздействие и т.д.
Осуществление любой из этих функций предполагает определенную внутреннюю организацию знаковой системы, т.е. наличие различных знаков и законов их сочетания. Таким образом, представляется исключительно важным вычленение существенного аспекта, звена, знака при построении или исследовании сформированной модели на предмет, в частности, адекватности моделируемому объекту.
Между моделью и исследуемым объектом должно иметь место некое сходство, которое может заключаться в подобии их физических характеристик, в схожести функций, выполняемых объектом и моделью, математического описания модели и объекта [6]. Степень «родства» и глубину отождествления модели и объекта определяет контекст, в рамках которого осуществляется сам процесс моделирования.
Любая модель представляет собой некую абстракцию, ибо при формировании модели акцент делается на вполне определенной части моделируемого объекта в соответствии с рассматриваемым контекстом, абстрагируясь при этом от остальных, несущественных для данного случая. Тем самым вычленяется выбранное для исследования проявление некого единого объекта. Было бы несомненным упрощением сведение модели к некому отражению или воспроизведению объектов исследования. Процесс научного познания протекает в различных направлениях, в соответствии с которыми изменяются функции модели и этапы построения, к которым относят: эвристический, познавательный, прагматический, интегрирующий, оптимизирующий. Структура и этапы процесса построения модели во многом сходны с процессом абстрагирования, что, несомненно, позволяет говорить о своеобразном взаимопроникновении мыслительных операций (МО) и метода научного познания [3]. Так, например, при формировании МО «абстрагирование» возможно использование в образовательном процессе объектов с пошаговым упрощением структуры и содержания (см. схему 1).
Схема 1.
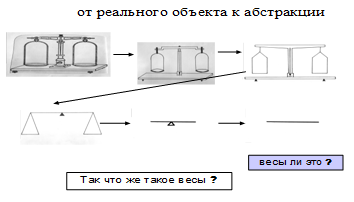
В результате абстрагирования мы получили некую модель реального объекта, в данном случае аналитических весов. Следует подчеркнуть, что «узнаваемость» в рисунке весов сохранилась, однако специфические особенности аналитических весов в процессе абстрагирования утеряны. Это произошло при переходе от третьего к четвертому рисунку. Таким образом, если бы была поставлена задача получить некую модель аналитических весов, следовало бы остановиться на третьем рисунке-этапе. В данном же случае, в соответствии с задачей, была построена в высшей степени абстрактная модель весов. Дальнейшие действия, связанные с возможным условным упрощением, привели бы к лишению полученной модели специфических особенностей исходного объекта. Например, изъяв из изображения опору плеч весов, мы превратим весы в некую прямую линию, не имеющую отношение к процессу взвешивания.
Следует отметить, что модели, используемые в образовательном процессе, являясь своеобразным отображением моделей, построенных в рамках соответствующей науки, представляют собой некое необходимое и неотъемлемое звено в усвоении теоретических знаний. Сам же процесс моделирования, процесс построения модели представлен в конкретных учебных дисциплинах в явно усеченном виде, с использованием лишь отдельных элементов многомерного процесса моделирования:
- составление плана параграфа или некого произведения,
- построение графиков (без акцентов на процессе),
- использование содержательных форм заданий типа: «Чем мы можем заменить...» и т.д.
В большинстве случаев механизм построения модели как, несомненно, самое ценное с позиции методологии науки, к сожалению, опускается. Задания, предполагающие реализацию этапов моделирования, встречаются не часто. Содержательные формы заданий «предложите способ ...» или «предложите средство...», которые в значительной степени могут создать условия для успешного разрешения указанной проблемы, редко можно встретить в практике работы учителей вне зависимости от их специальности.
Рассмотрим пример, иллюстрирующий некоторые возможности указанных содержательных форм заданий для организации деятельности учащихся в соответствии с вычлененным механизмом процесса моделирования, тем самым, создавая условия для целенаправленного обучения приему учебной работы, соответствующему процессу построения модели. Остановимся на содержательной форме задания «предложите способ...», создающей условия для реализации процесса построения некой модели и моделирования процесса получения требуемого результата на основе сформированной модели.
Задание. «Предложите способ определения веса одной капли воды, если у вас имеются: большой стеклянный сосуд с водой, пробирка, нитка, гиря 10 г, пипетка и фломастер».
Данное задание не предполагает проведение эксперимента с реальными объектами, хотя это возможно в рамках решения экспериментальных задач. В данном случае в качестве решения предполагается описание некой экспериментальной установки, сформированной на основе перечисленных предметов, и последовательности действий, приводящих к запрашиваемому результату (текст), либо рисунок, чертеж с пояснениями.
В качестве первичной модели для последующего детального построения могут быть выбраны «простые механизмы» - рычаг и блок. При этом применительно к рычагу в качестве опоры обычно используют край большого стеклянного сосуда, фломастер - в качестве самого рычага, а гирю и пробирку подвешивают на разные концы его. При рассмотрении блока в качестве основы для построения первичной модели, фломастер используется как «вращающийся» элемент - блок. Либо через фломастер перебрасывают нить и заставляют ее скользить по нему. Гиря и пробирка при этом привязаны к разным концам нити. Все дальнейшие действия аналогичны рассмотренным при построении модели с рычагом. Однако и в данном случае возможно вычленить некие детали, части в сформированной экспериментальной установке, которые не позволят принять предлагаемый вариант. При рассмотрении фломастера как блока, весьма проблематично заставить его вращаться вокруг своей оси в связи с отсутствием таковой. Если же нить просто перекинута через фломастер и должна таким образом скользить, то очень сложно учесть величину возникающей силы трения скольжения, что существенно при получении результата. И, наконец, самым главным является отсутствие дополнительных гирь для уравновешивания пробирки, что является определяющим в принятии данной модели за основу. Если же в качестве первичной модели избрать некий вариант гидростатических весов, то после детальной проработки, возможно получение вполне корректного результата. Данная модель предусматривает использование всех предложенных предметов. Предполагается следующая последовательность действий:
- в пробирку поместить гирю 10 г с привязанной к ней ниткой,
- пробирку с гирей опустить в большой сосуд с водой,
- отметить с помощью фломастера глубину погружения пробирки в воду,
- вынуть гирю из пробирки,
- накапать в пробирку, считая капли, с помощью пипетки воды столько, чтобы пробирка погрузилась в воду до отмеченного уровня, (значит, вес пробирки вновь увеличился на 10 г),
- разделив 10 г на число капель в пробирке, получаем вес одной капли воды.
Иллюстрирующий рисунок экспериментальной установки достаточно прост для схематичного изображения и его выполнение не вызывает у школьников затруднений.
Если попытаться проанализировать результаты выполнения данного задания школьниками (более 3 тыс. работ), то можно сделать вывод о том, что в представленном варианте с заданием справляется до 40 % учащихся. Если же в тексте задания «фломастер» заменить на «карандаш», то количество правильных решений уменьшается до 20-25%. Если задание переформулировать: «Предложите способ определения веса одной капли воды без использования весов», то верных решений окажется не более 12-15 %. Из бесед с учащимися было выяснено, что наличие в перечне приборов фломастера их наталкивало на мысль о возможности нанесения на стекле (сосуд или пробирка) каких-либо пометок, рисок, а «...карандаш на стекле не пишет...». Тем самым они отметали возможность использования карандаша как пишущего элемента и искали ему несколько иное применение. В случае же с переформулированным заданием для учащихся вообще отсутствовали ориентиры для актуализации знаний, что вызывало значительные затруднения при решении задачи [4].
Таким образом, акцентирование внимания учащихся на существенных, знаковых для данного контекста аспектах процесса моделирования или анализа сформированной модели положительно сказывается на формировании основ моделирования как одной из структурных составляющих механизма познавательного процесса [5,6].
На схеме 2 представлен пример из методических материалов, ориентированных на целенаправленное формирование умений по определению наиболее значимых характеристик исследуемого объекта.
Схема 2.
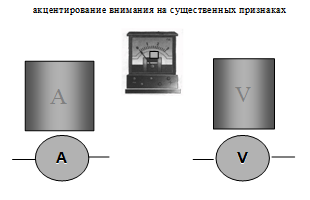
Внешне школьные демонстрационные амперметр и вольтметр очень похожи. Отличие заключается лишь в «буквенном» обозначении А и V, которое закрыто. Предлагается определить принадлежность данного прибора. Тем самым акцентируется внимание на наиболее существенном в данном случае признаке, что позволяет корректно осуществить процесс идентификации прибора. Аналогичным образом выстроена система обучения идентификации физических тел, явлений, процессов, величин. Указанные объекты следует рассматривать как «внешние» по отношению к субъектам образовательного процесса. Современные стандарты для средней школы предусматривают формирование весьма сложного «умения» по самоидентификации личности ученика.
Представленный подход и примеры соответствующих методических материалов позволяют сделать вывод о возможности реализации следующей логической цепочки (см. схема 3).
Схема 3.
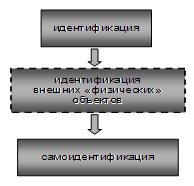
На базе формируемого механизма идентификации физических объектов выстраиваются основы самоидентификации различного уровня. Реализация логической последовательности семиотического характера «факт, знак, тест (рисунок), интерпретация, значение» также, несомненно, может быть использована в образовательном процессе по физике применительно к моделированию.
Рецензенты:
Грабов В.М., д.ф.-м.н., профессор Российского государственного педагогического университета им. А.И. Герцена, г. Санкт-Петербург.
Ходанович А.И., д.п.н., профессор, заведующий кафедрой математики и информатики Санкт-Петербургского государственного университета кино и телевидения, г. Санкт-Петербург.
Библиографическая ссылка
Комаров Б.А. ЭЛЕМЕНТЫ СЕМИОТИЧЕСКОГО ПОДХОДА В МОДЕЛИРОВАНИИ ПРИ ОБУЧЕНИИ ФИЗИКЕ В СОВРЕМЕННОЙ ШКОЛЕ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=14697 (дата обращения: 26.04.2024).



