В последние годы в специализированных журналах и книгах по робототехнике растет количество работ, в которых рассматриваются различные проблемы группового управления автономными мобильными роботами и микророботами, что связано с ожидаемым расширением возможностей роботов при их согласованном (коллективном) использовании для решения поставленных задач [7-10]. В большинстве работ предполагается использование групп роботов в экстремальных условиях или опасных средах, поэтому часто в дополнение к общей задаче управления движением появляются проблемы планирования движения в нестационарном рабочем окружении на стратегическом, тактическом и исполнительном уровнях: непредсказуемое изменение окружающей обстановки, наличие подвижных препятствий и т.д. На сегодняшний день для планирования движений часто используются либо приближенные методы, либо подходы на основе интеллектуальных алгоритмов. Приближенные методы основаны на дискретизации рабочего пространства, когда вместо описания рабочей области и препятствий непрерывными функциями используются дискретные модели внешней среды в сочетании с методами динамического и целочисленного программирования, потенциальных функций и т.д. Интеллектуальные методы также используют дискретное представление рабочего пространства, но при этом включают различные типы алгоритмов на основе технологий мягких вычислений: искусственных нейронных сетей, нечеткой логики и эволюционных алгоритмов.
Ранее авторами уже рассматривались вопросы сравнительного анализа алгоритмов планирования [3, 5], но за последнее время были получены новые результаты, поэтому в статье приводится краткое описание и сравнительный анализ некоторых приближенных и интеллектуальных алгоритмов планирования траекторий, полученных в ходе последних модельных и полунатурных экспериментов; рассматриваются их достоинства и недостатки, а также даются рекомендации по использованию того или иного метода в зависимости от особенностей решаемой задачи и требований, предъявляемых к быстродействию алгоритма, оптимальности траектории, наличию сенсорной информации и т.д.
Приближенные методы планирования
Особенностью приближенных методов планирования является необходимость дискретизации рабочего пространства. При таком представлении рабочая область разбивается на конечное число прямоугольных элементарных областей, каждая из которых отмечается либо свободной, либо занятой препятствием. Одним из первых протестированных приближенных методов являлось представление «пространство-время» [11]. Для решения задачи планирования в рассматриваемом методе применяется принцип динамического программирования Р. Беллмана, заключающийся в пошаговой процедуре нахождения оптимальной траектории, начиная с конечной точки. Достоинством такого подхода является универсальность по отношению к виду препятствий и способу их движения. При небольших размерностях дискретного рабочего пространства алгоритм планирования может быть реализован на ПЭВМ без существенных аппаратно-временных затрат, так как все вычислительные операции могут быть сведены к целочисленным расчетам. При планировании траекторий движения группы роботов применяется назначение приоритетов для каждого робота в группе, и задача планирования движения в многомерном пространстве преобразуется в задачу последовательного планирования траектории для каждого из роботов в пространстве с небольшой размерностью.
Основные сложности использования данного подхода связаны с нерациональным использованием вычислительных ресурсов при групповом планировании движений роботов в задачах с большой дискретностью рабочего пространства. К примеру, при размерности поискового пространства 100х100х100 целевая функция вычисляется для каждого элемента матрицы движения (то есть, 106 раз). Поэтому аппаратные затраты, связанные с заполнением матрицы, оказываются неоправданно высокими.
Из других приближенных подходов можно отметить методы на основе потенциальных функций, поиска пути по графу и целочисленного программирования. Аппаратные требования при использовании метода потенциальных функций возрастают пропорционально количеству роботов в группе и определяются необходимостью применения высокопроизводительных вычислений для численного интегрирования потенциальных функций сложного вида. Методы целочисленного программирования также требуют большой объем вычислений, из-за чего приходится увеличивать шаг дискретизации, что приводит к уменьшению точности нахождения оптимальных траекторий движения.
В условиях коллективного управления, для которых характерны стохастические процессы во внешней среде и априорная неопределенность условий функционирования, использование приближенных методов возможно лишь при решении задач планирования на стратегическом уровне с минимумом информации об окружающей обстановке и часто с огрублением полученных данных. Поэтому для решения задач планирования траекторий на тактическом и исполнительном уровнях перспективным видится использование подходов, базирующихся на различных типах интеллектуальных алгоритмов.
Планирование на основе интеллектуальных алгоритмов
Для задач планирования траекторий в недетерминированной среде высокую эффективность демонстрируют системы принятия решений с элементами искусственного интеллекта, в частности, с использованием генетических алгоритмов (ГА), ориентированных на быстрые решения многокритериальных задач поиска экстремумов. Задача планирования траекторий для группы роботов, базирующаяся на применении ГА, сводится к формированию модели внешней среды, кодированию потенциальных решений, генерации начальной популяции и определению критериев выживания популяции на каждом эволюционном этапе [4].
Одним из наиболее важных этапов является кодирование потенциальных решений. Если в качестве индивидуумов рассматривать маршруты движения по ячейкам дискретного трехмерного рабочего пространства, то хромосома представляет собой последовательность узлов, образующих траекторию движения. При этом каждый i-ый узел будет содержать гены, представляющие собой координаты в виде индексов xi и yi соответствующей ячейки, а также индекс момента времени ti, в котором агент достигнет эту ячейку (рис. 1). Гены, соответствующие времени и расположенные в последовательных узлах хромосомы, отличаются на единицу.
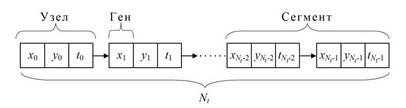
Рис. 1. Кодировка маршрута движения в хромосоме
Для полученного множества потенциальных решений применяются как стандартные генетические операторы – скрещивания и мутации, так и специфические, характерные для траекторных задач, операторы ‑ спрямления и сглаживания, результатом работы которых являются получение новых хромосом и отбор среди них лучших решений для следующего поколения. Эти действия повторяются итеративно, пока полученное решение не будет удовлетворять заданному интегральному критерию, который формируется как взвешенная сумма следующих параметров найденных траекторий: длина маршрута, время перемещения в заданную точку и т.д.
В последние годы широкое распространение также получило использование нейросетевых алгоритмов для решения технических задач в самых различных областях науки и техники, так как они структурно поддерживают принципы параллельной обработки сигналов. Решение задачи планирования траекторий на базе нейронных сетей обычно сводят к следующим этапам [1, 6]: формализация задачи планирования; выбор топологии сети; отображение энергетических взаимодействий нейронов в сети в виде нейронной карты (поверхности); расчет полной траектории в виде некоторой процедуры «восхождения» к вершине поверхности (цели).
Выбор топологии нейронной сети определяет функции расстояния, используемые для расчета расстояния между нейронами в слое. Функция расстояния между нейронами i и j в описываемой сети есть функция евклидового расстояния ![]() :
:
![]() ,
,
где [i] и [j] – векторы состояний i-го и j-го нейронов соответственно.
Для сети Хопфилда кроме ортогональной топологии можно использовать гексагональную с семью нейронами в нейронной области, то есть 6-ю возможными соседями для каждого нейрона (рис. 2).
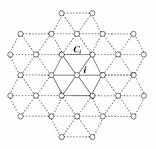
Рис. 2. Гексагональная топология сети
Дальнейшее решение задачи планирования определяется отображением энергетических взаимодействий нейронов в сети в виде нейронной карты. Для этого координаты цели, а также информация об окружающей среде подаются на вход сети Хопфилда. Нейроны сети входят в состояние равновесия и принимают собственные значения энергии (в зависимости от функции активации). Взаимодействия нейронов построенной сети обусловлены динамикой и архитектурой самой сети, а также конфигурацией окружающего пространства и координатами цели, которая является точкой активации. Значения энергии нейронов на данной нейронной области (ландшафт активации) поступают на вход блока генератора траектории, который, в свою очередь, и выполняет расчет и планирование траектории.
 Другие подходы, которые также получили в последние годы широкое распространение, используют методы на основе нечетких и нейронечетких алгоритмов. Основным преимуществом использования нечетких алгоритмов в задачах планирования траекторий является их низкая требовательность к аппаратным ресурсам [2]. Основными этапами решения задачи планирования для синтеза нечеткого регулятора являются: определение входов и выходов системы; задание функций принадлежности и разработка нечетких правил выводов. Входным и выходным сигналам нечеткого регулятора соответствуют логико-лингвистические переменные, значения которых определяются термами-множествами. База знаний нечеткой системы состоит из продукционных правил и отражает зависимость между входными и выходными термами-множествами. Для нечеткой системы мультиагентного планирования выбор нужного правила будет определяться угловым отклонением мобильного робота от цели и наличием свободных областей в рабочей зоне. В базе правил в первую очередь выполняется поиск по переменной «цель», что позволяет эффективнее использовать вычислительные ресурсы бортовой микроЭВМ. Аналогично строятся базы нечетких правил управления для других возможных ситуаций расположения цели относительно робота (цель перед роботом и слева, цель перед роботом и справа, цель слева, цель справа и т.д.).
Другие подходы, которые также получили в последние годы широкое распространение, используют методы на основе нечетких и нейронечетких алгоритмов. Основным преимуществом использования нечетких алгоритмов в задачах планирования траекторий является их низкая требовательность к аппаратным ресурсам [2]. Основными этапами решения задачи планирования для синтеза нечеткого регулятора являются: определение входов и выходов системы; задание функций принадлежности и разработка нечетких правил выводов. Входным и выходным сигналам нечеткого регулятора соответствуют логико-лингвистические переменные, значения которых определяются термами-множествами. База знаний нечеткой системы состоит из продукционных правил и отражает зависимость между входными и выходными термами-множествами. Для нечеткой системы мультиагентного планирования выбор нужного правила будет определяться угловым отклонением мобильного робота от цели и наличием свободных областей в рабочей зоне. В базе правил в первую очередь выполняется поиск по переменной «цель», что позволяет эффективнее использовать вычислительные ресурсы бортовой микроЭВМ. Аналогично строятся базы нечетких правил управления для других возможных ситуаций расположения цели относительно робота (цель перед роботом и слева, цель перед роботом и справа, цель слева, цель справа и т.д.).
Наиболее важной отличительной чертой алгоритмов планирования на основе нечеткой логики являются умеренные затраты машинного времени и оперативной памяти микроЭВМ. Вычислительные затраты также практически не зависят от размерности матрицы конфигурации рабочей зоны, а оптимизация используемого объема памяти микроЭВМ для больших размерностей рабочей области может быть достигнута отображением в матрице локальной зоны робота.
Сравнение методов планирования
Все выше рассмотренные методы планирования траекторий были реализованы в виде моделей, алгоритмического и программного обеспечений, что позволило провести ряд модельных и полунатурных экспериментов, результаты которых представлены в таблице 1.
Таблица 1
Результаты тестирования алгоритмов планирования
|
Метод планирования Параметры
|
Динамическое программирование |
Генетические алгоритмы |
Нейронные сети |
Нечеткая логика |
|
Размерность дискретного рабочего пространства |
от 10x10 до 20х20 |
от 10x10 до 100х100 |
от 10x10 до 100х100 |
от 10x10 до 1000х1000 |
|
Коэффициент дискретизации, η |
1,1÷1,5 |
1,1÷1,5 |
1,1÷1,5 |
1,1÷1,5 |
|
Количество роботов в группе |
до 5 |
до 50 |
до 100 |
до 1000 и более |
|
Затраты машинного времени на поиск траектории в рабочем пространстве 20х20 в группе из 5 роботов (CPU Intel Core i5-3570) |
250 мс |
21 мс |
110 мс (3-5 мс при мультиканальной обработке) |
<1 мс |
|
Затраты машинного времени на инициализацию алгоритма |
300 мс (заполнение начальной матрицы) |
3 мс |
3100 мс (обучение нейронной сети) |
1 мс (инициализация базы знаний) |
|
Сенсорная информация |
полная конфигурация рабочей области |
полная конфигурация рабочей области |
полная конфигурация рабочей области |
в ближней окрестности робота |
|
Критерии оптимальности траектории |
- по длине; |
- по длине; |
- по длине; - по гладкости |
- по гладкости; |
|
Управление взаимодействием роботов |
централизованное |
централизован-ное |
централизо-ванное, групповое |
мультиагентное, групповое (рой) |
Для корректности проводимых исследований для дискретизации рабочего пространства был рассчитан единый минимальный размер квадратной ячейки, длина сторон ΔS которой выбирается из условия обеспечения алгоритмом бесконфликтного движения – исключения столкновений роботов между собой, столкновений со стационарными препятствиями, а также выход за пределы рабочего пространства. Величину шага дискретизации ΔS выбирали используя следующее выражение:
ΔS = η · Lmin,
где Lmin – минимальный линейный размер наименьшего по габаритам робота, функционирующего в пределах рабочей области, или препятствий, расположенных в зоне движения роботов; η – коэффициент шага дискретизации, характеризующий достижимую безопасность движения в заданной среде. Как показали результаты моделирования, при выборе величины коэффициента η в диапазоне 1,1÷1,5 обеспечивается бесконфликтное движение с сохранением возможности эффективного планирования с точки зрения гладкости, оптимальности по времени и длине маршрута. Выбор шага дискретизации в соответствии с этой рекомендацией также позволяет получить поисковое пространство с наименьшей размерностью, при которой реализуется бесконфликтное движение мобильных роботов, а значит достигается эффективность работы каждого алгоритма.
Исходя их полученных данных, при массовом применении мобильных роботов, когда коллективы насчитывают сотни мобильных устройств и практически исключается централизованное управление, наиболее перспективным видится использование методов планирования траекторий на основе нечеткой логики. При построении групп роботов меньших размеров, когда существует вышестоящий уровень управления (координации) коллектива, актуальной становятся задачи не только локального планирования. Поэтому, несмотря на сложность реализации бортовой системы планирования-управления на основе генетических алгоритмов или нейронных сетей, они часто используются и демонстрируют более высокое качество генерируемых траекторий для тактического уровня. Последние эксперименты по модификации нейросетевых алгоритмов с использованием технологий мультипоточных вычислений показали результаты, сравнимые по быстродействию и аппаратными требованиями с нечеткими системами планирования.
Метод динамического программирования наиболее затратен и требователен к ресурсам, что обусловлено необходимостью последовательного планирования траектории для каждого из роботов, поэтому его применение возможно только на стратегическом уровне при работе с грубыми первичными данными об окружающей обстановке.
Заключение
При решении задач планирования с учетом особенностей группы мобильных роботов как объекта управления (многосвязность, многомерность и стохастичность поведения) необходимо учитывать требуемый уровень детализации траекторий и выбирать наиболее эффективное решение. При грамотном выборе области применения и некоторой модификации практически любой из рассмотренных выше алгоритмов планирования траекторий может продемонстрировать требуемое качество даже при решении задач более высокого или более низкого уровней.
При выборе необходимо учитывать также и некоторые специфические особенности применяемых методов. Так генетические алгоритмы позволяют избежать проявления локальных экстремумов; нейросети могут быть реализованы с использованием нейроускорителей, а также обладают способностью быстрой адаптации с организацией пере- или дообучения в реальном времени. Основной причиной, обеспечивающей некоторые преимущества нечетких алгоритмов в задачах планирования, является их низкая требовательность к аппаратным ресурсам в сочетании с высокой скоростью отклика.
Работа по данной тематике выполнялась в рамках Программы №1 фундаментальных исследований ОЭММиПУ РАН «Научные основы робототехники и мехатроники».
Рецензенты:
Мунасыпов Р.А., д.т.н., профессор, заведующий кафедрой «Мехатронные станочные системы», ФГБОУ ВПО Уфимский государственный авиационный технический университет, 450000, Республика Башкортостан, г. Уфа;
Жернаков С.В., д.т.н., профессор, заведующий кафедрой «Кафедра электроники и биомедицинских технологий», ФГБОУ ВПО Уфимский государственный авиационный технический университет, г. Уфа.
Библиографическая ссылка
Даринцев О.В., Мигранов А.Б. ОБЛАСТИ ПРИМЕНЕНИЯ ПРИБЛИЖЕННЫХ И ИНТЕЛЛЕКТУАЛЬНЫХ МЕТОДОВ ПЛАНИРОВАНИЯ ТРЕКТОРИЙ ДЛЯ ГРУПП МОБИЛЬНЫХ РОБОТОВ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16542 (дата обращения: 26.04.2024).



