В работах [1; 2] было показано, что в качестве структурного модуля при структурно-кинематическом синтезе плоских рычажных механизмов можно использовать четырехзвенную исходную кинематическую цепь (ИКЦ). Такой подход к синтезу плоских механизмов позволяет свести задачу их структурно-кинематического синтеза к решению задачи синтеза ИКЦ, что очень удобно для автоматизации проектирования механизмов. В данной работе показано, что указанный подход можно распространить на задачу структурно-кинематического синтеза пространственных рычажных механизмов.
Представлено решение задачи синтеза пространственной ИКЦ со сферическими кинематическими парами и показано ее использование в качестве структурного модуля при структурно-кинематическом синтезе пространственных рычажных механизмов по заданным положениям входного и выходного звеньев. Метод решения задачи синтеза ИКЦ со сферическими парами основан на введении двух подвижных тел, неизменно связанных с входным и выходным звеньями, и в отыскании круговых точек в относительном движении этих тел [3].
Цель исследования: структурно-параметрический синтез пространственных рычажных механизмов.
Материал и методы исследования опираются на основы высшей математики и теории механизмов и машин.
Постановка задачи. Пусть заданы N конечноудаленных положений двух твердых тел ![]() и
и ![]() ,
, ![]() , где
, где ![]() - эйлеровы углы относительно неподвижной системы координат OXYZ систем координат Ax'y'z' и Dx²y²z², неизменно связанных с телами Q1 и Q2 соответственно.
- эйлеровы углы относительно неподвижной системы координат OXYZ систем координат Ax'y'z' и Dx²y²z², неизменно связанных с телами Q1 и Q2 соответственно.
Требуется найти точки ![]() в неподвижной системе координат,
в неподвижной системе координат, ![]() тела Q1 и
тела Q1 и 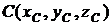 тела Q2 такие, чтобы расстояние между точками В и С во всех положениях тел Q1 и Q2 мало отличалось от некоторой постоянной величины R (рис. 1).
тела Q2 такие, чтобы расстояние между точками В и С во всех положениях тел Q1 и Q2 мало отличалось от некоторой постоянной величины R (рис. 1).
Решение задачи. Введем взвешенную разность для i-го положения тел в виде:
![]() (1)
(1)
Она является функцией десяти параметров: XA, YA, ZA, xB, yB, zB, R, xC, yC, zC. Группируя эти параметры по четыре с общим параметром R, взвешенную разность представим в трех различных формах:
![]() (2)
(2)
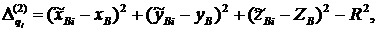 (3)
(3)
![]() (4)
(4)
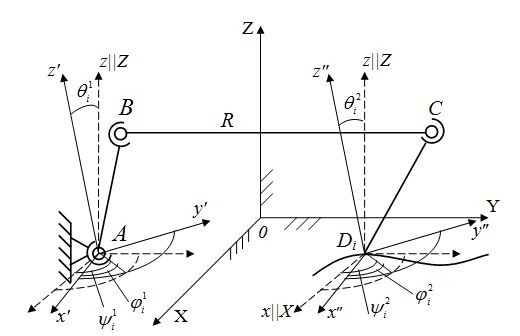
Рисунок 1. Исходная кинематическая цепь со сферическими парами.
здесь:
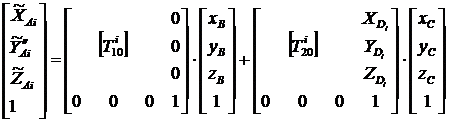 , (2/)
, (2/)
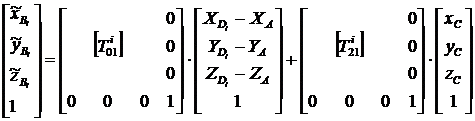 , (3/)
, (3/)
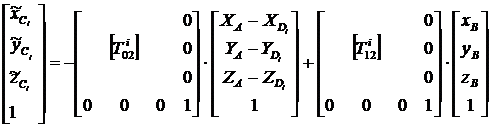 , (4/)
, (4/)
![]() - матрица перехода от k-той системы координат к j-той системе, определяемые как
- матрица перехода от k-той системы координат к j-той системе, определяемые как
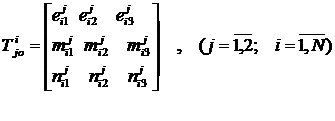 (5)
(5)
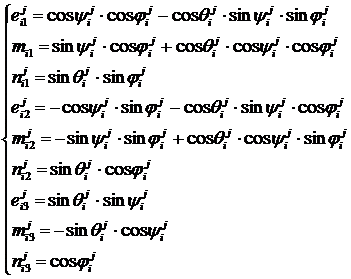 (6)
(6)
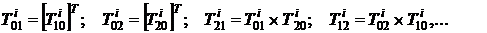 (7)
(7)
Необходимые условия минимума суммы квадратов взвешенной разности:
![]() (8)
(8)
можно записать в виде следующей системы уравнений:
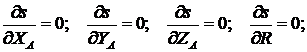 (9)
(9)
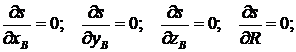 (10)
(10)
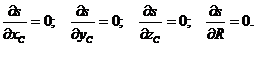 (11)
(11)
Из (9) с учетом (2) и (8) получим:
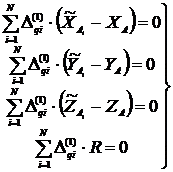 (12)
(12)
Допустим, что 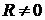 . Тогда из последнего равенства системы (12) следует, что
. Тогда из последнего равенства системы (12) следует, что
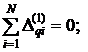 (13)
(13)
С учетом (13) система уравнений (12) принимает вид:
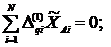
![]()
![]()
![]() (14)
(14)
Подставляя выражения для ![]() из (2) в систему (14), получим:
из (2) в систему (14), получим:
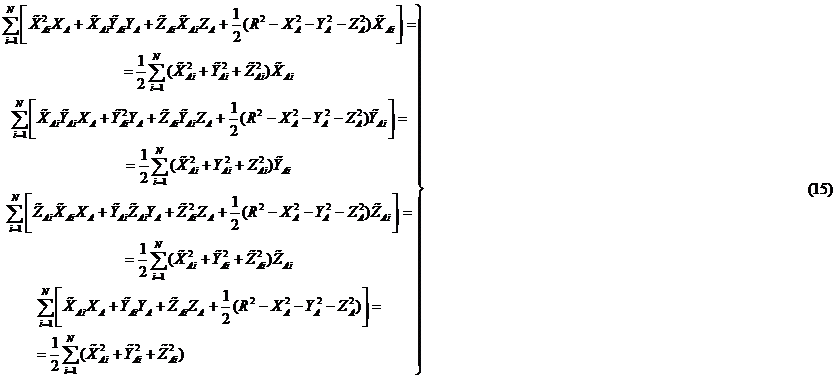
Система (15) линейна относительно переменных ![]() и
и 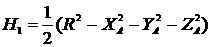 , поэтому ее можно записать в виде:
, поэтому ее можно записать в виде:
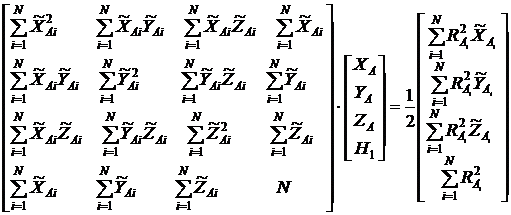 , (16)
, (16)
здесь ![]()
Решение этой системы по правилу Крамера при ![]() имеет вид:
имеет вид:
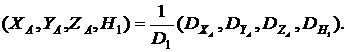 (17)
(17)
Аналогично из (10) с учетом (3) и (8) получим систему линейных уравнений относительно неизвестных ![]() :
:
 (18)
(18)
Решая эту систему по правилу Крамера при ![]() , получим:
, получим:
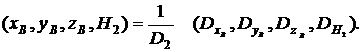 (19)
(19)
Из (11) с учетом (4) и (8) получим систему линейных уравнений относительно неизвестных xC, yC, zC, H3:
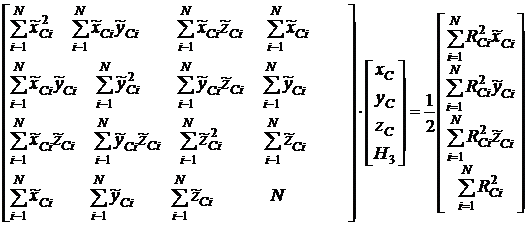 (20)
(20)
Отсюда находим xC, yC, zC, H3 при ![]() :
:
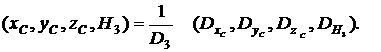 (21)
(21)
Исключая первые четыре неизвестных XA, YA, ZA, R на основе формулы (16), можно свести систему (9)-(11) к системе из шести уравнений с шестью неизвестными ![]() , которую удобно представить в виде:
, которую удобно представить в виде:
 (22)
(22)
Уравнения этой системы по виду совпадают с тремя уравнениями тринадцатой степени относительно трех неизвестных, приведенными в работе [4], хотя в данном случае имеем систему из шести уравнений относительно шести неизвестных. Решение системы (22) представляет трудоемкую задачу, поэтому гораздо эффективнее применять следующий алгоритм поиска минимума функции S:
1. Задаемся произвольно начальными точками ![]()
2. Решаем систему линейных уравнений (16) и определяем ![]()
3. Задаемся точками ![]()
4. Решаем систему уравнений (18) и определяем ![]()
5. Задаемся точками ![]()
6. Решаем систему уравнений (20) и определяем 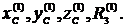
7. Далее циклически повторяем шаги (1-6), заменяя начальные точки В(0) и С(0) на найденные В(1) и С(1).
Применяя алгоритм, получим убывающую последовательность значений целевой функции ![]() имеющую предел, равный значению функции S в точке локального минимума. В результате решения задачи определяются точки
имеющую предел, равный значению функции S в точке локального минимума. В результате решения задачи определяются точки ![]() в неподвижной системе координат
в неподвижной системе координат ![]() , такие, что совмещая с ними звено ВС, получаем искомую ИКЦ в виде разомкнутой цепи ABCD.
, такие, что совмещая с ними звено ВС, получаем искомую ИКЦ в виде разомкнутой цепи ABCD.
Задавая в различных комбинациях часть искомых параметров синтеза, получим различные модификации ИКЦ.
1. Если заданы координаты точки ![]() и эйлеровы углы
и эйлеровы углы ![]() тела Q1 и координаты точки
тела Q1 и координаты точки ![]() и эйлеровы углы
и эйлеровы углы ![]() тела Q2 , то получим трехзвенную незамкнутую цепь ABCD (рис. 2).
тела Q2 , то получим трехзвенную незамкнутую цепь ABCD (рис. 2).
Необходимые условия минимума суммы S в данном случае принимают вид:
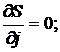 ( j = xB, yB, zB, R, xC, yC, zC);
( j = xB, yB, zB, R, xC, yC, zC);
и для нахождения минимума S можно использовать алгоритм, приведенный выше, учитывая, что параметры ![]() заданы и не требуют определения.
заданы и не требуют определения.
Если точки ![]() и
и ![]() фиксированы, то в результате синтеза ИКЦ получим пространственный четырехзвенник ABCD.
фиксированы, то в результате синтеза ИКЦ получим пространственный четырехзвенник ABCD.
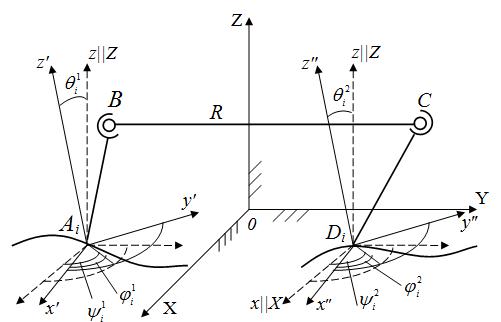
Рисунок 2. Трехзвенная кинематическая цепь.
2. Пусть заданы координаты ![]() точки С
точки С![]() Q2, координаты
Q2, координаты 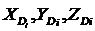 точки D тела Q2 и углы Эйлера
точки D тела Q2 и углы Эйлера ![]() тела Q1, а искомыми параметрами являются
тела Q1, а искомыми параметрами являются ![]()
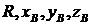 (рис. 3).
(рис. 3).
Необходимые условия минимума сумма S принимают вид:
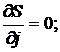 ( j = XA, YA, ZA, R, xB, yB, zB).
( j = XA, YA, ZA, R, xB, yB, zB).
Для нахождения минимума функции S можно опять использовать алгоритм, приведенный выше, учитывая, что ![]()
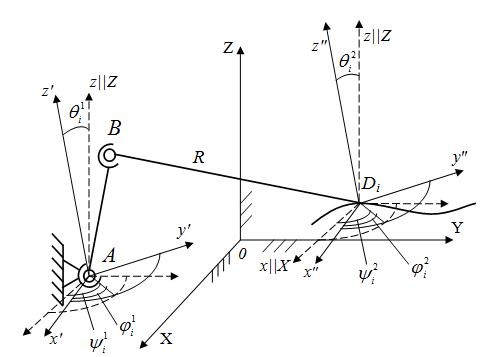
Рисунок 3. Трехзвенная кинематическая цепь.
3. Пусть заданы координаты ![]() = 0 точки В тела Q1 и координаты точки
= 0 точки В тела Q1 и координаты точки ![]() и эйлеровы углы
и эйлеровы углы ![]() тела Q2. Исходная задача сводится к определению сферы наименее удаленной от N положений фиксированной точки С тела Q2.
тела Q2. Исходная задача сводится к определению сферы наименее удаленной от N положений фиксированной точки С тела Q2.
Необходимые условия минимума суммы S:
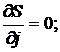 ( j = XA, YA, ZA, R, xC, yC, zC).
( j = XA, YA, ZA, R, xC, yC, zC).
Данная задача подробно исследована в работе [4]. Для ее решения можно применить и алгоритм, приведенный выше, полагая ![]() =0, но в этом частном случае алгоритм поиска минимума полностью совпадает с методом кинематической инверсии.
=0, но в этом частном случае алгоритм поиска минимума полностью совпадает с методом кинематической инверсии.
Результаты исследования и их обсуждение
Результаты исследования приведены конкретными решениями задач синтеза. Решена задача синтеза ИКЦ со сферическими кинематическими парами и их модификации, которые могут быть использованы как модули структурно-кинематического синтеза пространственных рычажных механизмов по заданным положениям входного и выходного звеньев.
Выводы
На основе задания двух подвижных тел проводится кинематический синтез механизмов по заданным положениям входного и выходного звеньев.
Рецензенты
-
Мендебаев Т.М., д.техн.н., профессор, заведующий кафедрой «Стандартизация, сертификация технологии машиностроительного производства», КазНТУ им. К.И. Сатпаева, г. Алматы.
-
Даусеитов Е.Б., д.техн.н., профессор кафедры «Прикладная механика и основы конструирования машин», КазНТУ им. К.И. Сатпаева, г. Алматы.
-
Антонов А.В., д.техн.н., профессор, декан факультета кибернетики, Обнинский институт атомной энергетики Национального исследовательского ядерного университета МИФИ, г. Обнинск.
Библиографическая ссылка
Косболов С.Б., Танжарикова Г.П., Рахматулина А.Б. ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ ПРОСТРАНСТВЕННЫХ РЫЧАЖНЫХ МЕХАНИЗМОВ НА ОСНОВЕ ИСХОДНОЙ КИНЕМАТИЧЕСКОЙ ЦЕПИ // Современные проблемы науки и образования. – 2012. – № 2. ;URL: https://science-education.ru/ru/article/view?id=6076 (дата обращения: 27.04.2024).



