Для обеспечения нормального функционирования сооружений в северных условиях необходим прогноз эволюции фронта промерзания-оттаивания грунта. Неправильный прогноз может отрицательно сказаться на состоянии фундамента здания. Фазовые переходы влаги имеют место также и в наружных конструкциях, построенных из материалов с микропорами. В осенний и весенний периоды опасны суточные колебания границы промерзания-оттаивания, вызывающие разрушение материала. Они также оказывают влияние на тепловой режим здания. Мы предлагаем новый приближенный метод моделирования таких колебаний, основанный на решении задачи теплопроводности без начальных условий.
Традиционной математической моделью явления теплопроводности в грунте с фазовым переходом является задача Стефана [5], которая для одномерной полубесконечной области имеет вид:
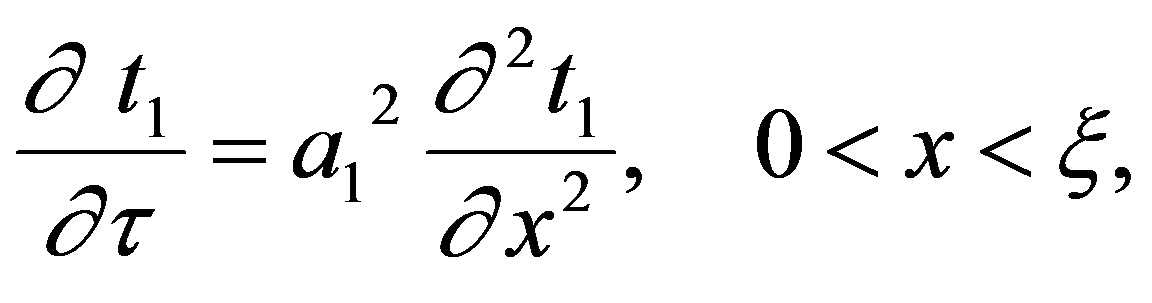 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
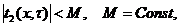 (4)
(4)
![]() (5)
(5)
где τ - время; x - пространственная координата; ξ - координата границы раздела фаз; t1 - температура в талой зоне; t2 - температура в мерзлой зоне; t* - температура фазового перехода; 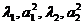 - коэффициенты теплопроводности и температуропроводности в талой и мерзлой зонах соответственно; ρ - удельная масса скелета грунта; k - скрытая теплота таяния воды; w - удельная влажность грунта.
- коэффициенты теплопроводности и температуропроводности в талой и мерзлой зонах соответственно; ρ - удельная масса скелета грунта; k - скрытая теплота таяния воды; w - удельная влажность грунта.
Условие ограниченности (4) является необходимым для обеспечения единственности решения задачи (1) - (3).
Задача вида (1) - (5) решается для определения положения границы оттаивания; она также входит в состав математических моделей, описывающих различные криогенные явления, например, морозное пучение грунта [3].
Аналитические решения этой задачи получены только для некоторых частных случаев. Для широкого класса нелинейных задач теплопроводности, включая задачу Стефана, может быть использована процедура последовательных приближений, представленная в работе [1]. Известно несколько численных схем решения задачи Стефана [5]. В научной периодике постоянно появляются работы, предлагающие новые подходы к решению этой задачи [4,6]. Разнообразие используемых методов является косвенным подтверждением того, что вопрос этот еще далеко не решен. Численное решение затруднено наличием при x=ξ особенности типа d-функции. Аппроксимация таких особенностей вносит плохо контролируемую погрешность. Во всяком случае, единого численного метода, пригодного для любых коэффициентов и краевых условий, пока не существует даже для одномерных задач.
В инженерной практике используются приближенные решения, основанные на упрощении задачи (1) - (5). Если предположить, что φ(x)=t*, то получаем так называемую однофазную задачу Стефана. Имеется в виду, что решение нужно искать только в талой зоне, так как при x>ξ при любом t температура известна t2≡t*. При f(t)=tc=const для однофазной и двухфазной (если φ(x)=const) задач получены удобные аналитические решения [5].
Дальнейшее упрощение возможно при квазистационарном подходе. Считаем, что граница x=ξ движется достаточно медленно, так что в каждый момент времени t поле температур в области 0<x<ξ можно считать стационарным. При квазистационарном решении одномерной однофазной задачи с f(τ)=tc получаем известную формулу Стефана. Если f(τ)≠const, то используются различные модификации первого и второго методов Л. С. Лейбензона, основанных также на квазистационарном подходе.
Популярность квазистационарного подхода заключается в том, что в этом случае решение краевой задачи в области 0<x<ξ имеет простой вид, а решение этой же задачи для уравнения (1) имеет вид ряда Фурье и при расчетах его использовать крайне неудобно.
Если f(τ) является периодической функцией (суточное, годовое колебание температуры поверхности грунта), то можно использовать в верхней зоне решение задачи теплопроводности без начальных условий, которое имеет замкнутый вид [5]. Некоторое усложнение в сравнении с квазистационарным методом компенсируется тем, что: 1) учитывается установившийся характер колебаний температуры, при котором начальные условия мало влияют; 2) при решении учитывается перераспределение тепла в верхней зоне.
Итак, вместо (1) - (5) решается следующая задача:
![]() (6)
(6)
t2(x,τ)=t*, ξ < x <∞, (7)
t1(0, τ)=A+B sin(wτ+ε), (8)
t1(ξ,τ)=t2(ξ,τ)=t*, (9)
где А, В, w, ε - константы.
При решении этой задачи положение границы фаз х=ξ считаем фиксированным при нахождении выражения для t1(х, τ). Закон движения границы x(t) находится из решения задачи Коши:
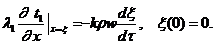 (10)
(10)
C учетом аналитического решения (6) - (9) для нахождения ξ(τ) получаем задачу:
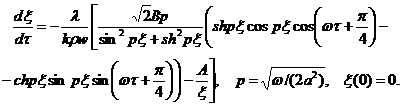 (11)
(11)
Данную методику можно применить для обоснования суточного режима отопления здания в районах с большой амплитудой суточных колебаний температуры воздуха.
Теплопотери здания через стену рассчитываются обычно по среднесуточным температурам. Для учета динамики суточных теплопотерь используются приближенные методы, основанные на квазистационарном подходе [2].
Предлагаемая методика позволяет учесть влияние нестационарного и нелинейного характера теплообмена в стене на теплопотери здания. Все строительные материалы содержат влагу, поэтому правильный теплофизический расчет для зимних условий должен учитывать, что суточные колебания температуры наружного воздуха приводят к колебанию межфазной границы ξ. Выделяемое или поглощаемое при этом джоулево тепло оказывает демпфирующее влияние, вследствие чего имеет место сдвиг фаз в колебаниях температуры наружной и внутренней поверхностей стен здания. Этот сдвиг оказывается настолько существенным, что его целесообразно учитывать при назначении суточного режима отопления.
С достаточным основанием можно считать, что колебания в наружном слое 0<x<ξ носят установившийся характер и их можно описывать задачей без начальных условий (6) - (9).
Размах колебаний величины ξ достаточно мал, поэтому задачу перемещения границы раздела фаз решается в однофазной постановке.
В слое ξ<x<Н (Н - толщина стены) влияние колебаний наружного воздуха значительно ослаблено, прежде всего фронтом фазового перехода, поэтому здесь мы принимаем квазистационарное приближение, то есть считаем, что тепловой поток при х=ξ равен тепловому потоку при х=Н. Задача (6) - (9) решается аналитически.
Расчеты показывают, что суточные колебания воздуха при наших допущениях не меняют суммарных теплопотерь здания. Однако эти колебания существенно влияют на сдвиг фаз в температурах при x=0 и x=H.
Очевидно, что этот сдвиг фазы равен сдвигу фазы температур на внешней и внутренней поверхностях стены. Сдвиг фазы ξ(τ) относительно t(τ), который главным образом определяется теплоемкостью и относительной влажностью материала, можно рассматривать как характеристику материала для выработки экономичного графика подачи тепла.
Рецензенты:
- Миронов Виктор Владимирович, д.т.н., профессор, проректор по научной и инновационной работе ТюмГАСУ, г. Тюмень.
- Чекардовский Михаил Николаевич, д.т.н., профессор, заведующий кафедрой «Теплогазоснабжения и вентиляции» ТюмГАСУ, г. Тюмень.
Библиографическая ссылка
Аксенов Б.Г., Карякина С.В., Шаповал А.Ф., Степанов О.А., Моисеев Б.В. МОДЕЛИРОВАНИЕ КОЛЕБАНИЙ ГРАНИЦЫ ПРОМЕРЗАНИЯ-ОТТАИВАНИЯ В ГРУНТАХ И НАРУЖНЫХ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЯХ // Современные проблемы науки и образования. – 2012. – № 2. ;URL: https://science-education.ru/ru/article/view?id=6088 (дата обращения: 26.04.2024).



