Введение
Течения идеального политропного газа, примыкающие к вакууму в условиях действия сил тяготения и Кориолиса, как и в [1], будут строиться в относительной цилиндрической системе координат. Соответствующая ей относительная декартова система координат имеет оси Ox, Oy, Oz, направленные соответственно на восток, север и вверх от поверхности. Будет полагаться, что точка O – начало декартовой системы координат – лежит на поверхности Земли в Северном полушарии на параллели с широтой ψ (рис. 1).
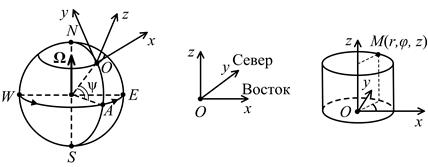
Рис. 1
Тогда в относительной декартовой системе координат постоянный вектор Ω – вектор угловой скорости Земли имеет вид: Ω=(0,Ω2, Ω3), Ω2= Ωcosψ, Ω3= Ωsinψ, где Ω=|Ω|.
Постановка задачи о распаде специального разрыва
Пусть в момент времени t = 0 трехмерная поверхность Г с уравнением
r = f(φ, z) отделяет идеальный политропный газ от вакуума. В задаче предполагается, что газ находится снаружи, а внутри полости – вакуум. Будут рассматриваться изэнтропические течения идеального политропного газа, то есть течения, у которых энтропия S=S0=const. Уравнение состояния берется в виде 
. Здесь p – давление, ρ – плотность газа, γ = const > 1 – показатель политропы газа. Отсюда следует, что скорость звука в газе 
.
В момент времени t=0 известны распределения параметров газа: 
– вектора скорости газа, где u0, v0, w0 – окружная, радиальная и вертикальная проекции вектора скорости; 
– скорости звука газа. Также предполагается, что на газ действует массовая сила с плотностью, являющейся суммой ускорения Кориолиса и ускорения свободного падения.
Функция f(φ, z), задающая поверхность Г, а также функции V0 , c0 предполагаются аналитическими. Также предполагается, что скорость звука в газе всюду больше нуля, в том числе 
.
В момент 
начинается движение газа, определяемое заданными при распределениями 
, которое в дальнейшем будем называть фоновым течением.
Кроме этого, предполагается, что в момент поверхность Г мгновенно разрушается и начинается истечение части газа в вакуум. Возмущения, возникшие в фоновом течении в результате мгновенного разрушения поверхности Г, распространяются по газу в виде волны разрежения, отделенной от фонового течения границей Г1, являющейся поверхностью слабого разрыва. С другой стороны волна разрежения примыкает к вакууму: 
, где Г0 – свободная поверхность, отделяющая волну разрежения от вакуума.
Требуется построить как фоновое течение, так и волну разрежения, а также найти законы движения Г1 и Г0.
Система уравнений, описывающая изэнтропические течения идеального политропного газа в условиях действия сил тяготения и Кориолиса, в цилиндрических координатах имеет следующий вид 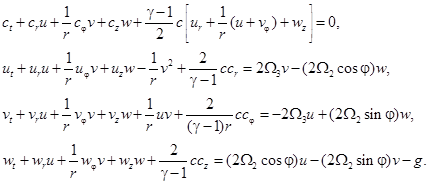[1]:
(1)
Начальные данные при t = 0 для системы (1) имеют вид:
(2)
Поскольку рассматриваемая система (1) является системой типа Ковалевской, а начальные данные – аналитические функции, то задача Коши (1), (2) по теореме Ковалевской [2] имеет при малых t единственное аналитическое решение, которое и задает фоновое течение: c = c(t, r, φ, z), 
.
По полученному фоновому течению построим закон движения поверхности слабого разрыва Г1 (
). В системе (1) введем новую независимую переменную 
, где 
– неизвестный закон движения Г1.
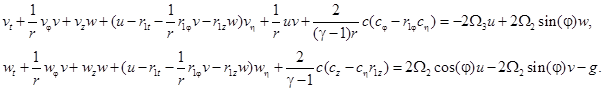
Из равенства нулю определителя перед производными по переменной η получим уравнение звуковой характеристики Г1:
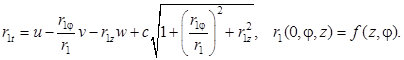(3)
Задача (3) имеет единственное аналитическое решение [3].
Имея закон движения Г1, получим значения параметров газа на ней
(4)
В дальнейшем будут предполагаться известными: фоновое течение, поверхность Г1, значения c1, V1, заданные с помощью аналитических функций.
Для построения волны разрежения, как и в [4; 5], поменяем ролями одну из независимых переменных r и одну из неизвестных функций c, то есть за независимые переменные возьмем t, c, φ, z, а за неизвестные функции – r, V. Якобиан такого преобразования 
. В результате этой замены вместо (1) получим систему:
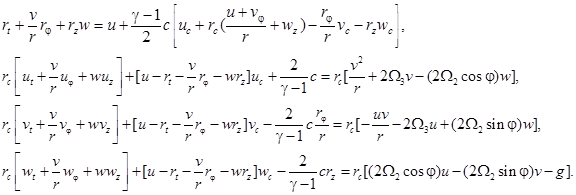(5)
Соответственно, условия (4) перейдут в
(6)
где 
— уравнение звуковой характеристики C+.
Течение в области между Г1 и Г0 (в области волны разрежения) будем строить как решение системы (5) с данными (6) на характеристике Г1. Поскольку Г1 – характеристика кратности один, то для получения единственного локально-аналитического решения необходимо задать одно дополнительное условие [4]:
(7)
Теорема. Существует t0 > 0 такое, что при 0< t ≤ t0 в некоторой окрестности Г1 существует единственное локально-аналитическое решение задачи (5)–(7) о распаде специального разрыва.
Доказательство. Доказательство теоремы состоит, как и в [6], в сведении задачи (5)–(7) к характеристической задаче Коши стандартного вида [7], для которой справедлив соответствующий аналог теоремы Ковалевской [7]. Для этого введем новую переменную: ξ=c-c1(t,φ,z), где c=c1(t,φ,z) — уравнение звуковой характеристики C+. Перепишем систему (5)
в векторном виде:
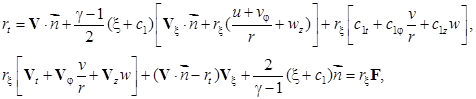(8)
где
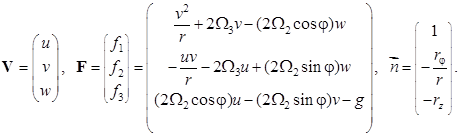
С помощью тождественных преобразований в системе (8) исключим из первого уравнения Vξ. Тогда систему (8) можно представить в виде
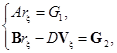(9)
где 
,
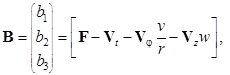
Поскольку 
и 
, то есть задача будет характеристической при 
.
Поскольку значения газодинамических параметров на C+ взяты из решения задачи (1)–(2) — из фонового течения, – необходимые условия разрешимости выполняются автоматически (см. условие (3)):
(10)
Переход к квазилинейной системе
Далее теорема доказывается сведением задачи (5)–(7) к характеристической задаче Коши стандартного вида. Для этого от системы (9) надо перейти к квазилинейной системе.
Для перехода к квазилинейной системе к неизвестным функциям r, u, v, w введем дополнительные функции r1= rt, u1= rt, v1= vt, w1= wt, r2= rφ, u2= uφ, v2= vφ, w2= wφ, r3= rz, u3= uz, v3= vz, w3= wz, а также 
. Всего получается 17 неизвестных функций.
С учетом новых неизвестных функций система (9) перепишется в виде:
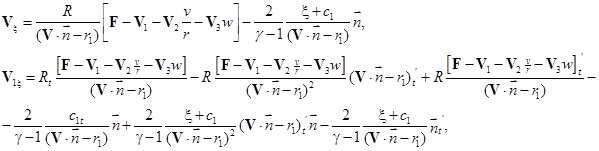
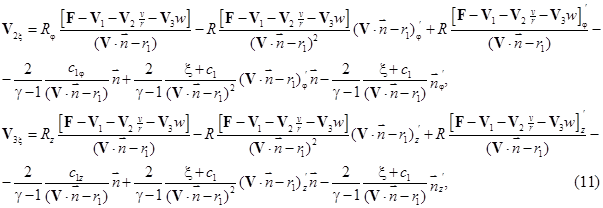
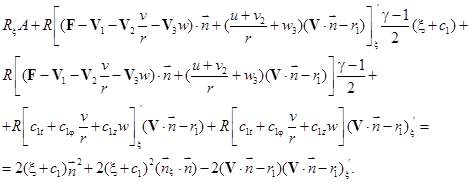
Здесь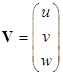 
, 
, 
, 
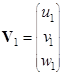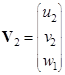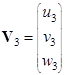. Кроме того,
Очевидно, что первые 16 уравнений полученной системы (11), записанные в нормальной форме, являются квазилинейными, то есть коэффициенты перед производными зависят только от переменных и неизвестных функций. Семнадцатое уравнение системы (11) является характеристическим и тоже квазилинейным. Подробный вид производных по переменной ξ в этом уравнении не приводится из-за громоздкости.
Постановка граничного и начальных условий для квазилинейной системы
Сначала поставим граничное условие при t = 0 для функции R. Граничное условия вертикали (7): 
Продифференцируем это равенство по переменной 
. Будем иметь 
или для неизвестной функции R
(12)
Поставим начальные условия. Значения вновь введенных неизвестных функций при 
() берутся из значений газодинамических параметров на звуковой характеристике Г1(6):
Поскольку переменные t, φ, z являются внутренними переменными этой поверхности, из начальных условий можно вычислить любую производную. Эти значения будут начальными условиями для новой квазилинейной системы, кроме неизвестной функции R.
(13)
Поскольку начальные условия (6) заданы аналитическими функциями r1 и V1, то и условия (13) будут аналитическими. Чтобы получить начальное условие при 
для функции R, в последнем уравнении системы (11) положим . Получим
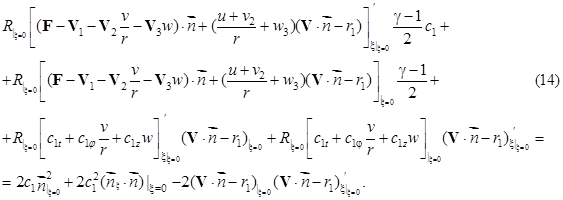
В полученное уравнение функция 
не входит, так как 
. Для простоты восприятия нижний индекс 
в дальнейшем будем опускать. Введем обозначение 
. Перенесем в левую часть равенства (14) только те слагаемые, которые содержат функции 
, 
, 
,
. В результате уравнение (14) примет вид
. (15)
С начальным условием при t = 0:
. (16)
Начальное условие (16) для функции 
получается из граничного условия (12).
Выражения Q6, L имеют вид: 
. Выражения Q1, Q2, Q3, Q4, Q5 не приводятся из-за громоздкости. Поскольку коэффициенты Q1, Q2, Q3, Q4, Q5, Q6, Q7, Q8, L при вычисляются из начальных условий, а начальные условия являются аналитическими функциями и 
, то задача (15)–(16) по теореме Ковалевской [2] имеет единственное аналитическое решение. Зная это решение, для функции R в системе (11) поставим начальное условие при
(17)
Таким образом, для системы (11) поставлены аналитические начальные условия на звуковой характеристике () (13), (17) и граничное условие (12). Следовательно, задача (11), (12), (13), (17) является характеристической задачей Коши стандартного вида и имеет единственное локально-аналитическое решение [7]. Теорема полностью доказана.
Рецензенты:
Баутин Сергей Петрович, доктор физ.-мат. наук, профессор, Уральский государственный университет путей сообщения, г. Екатеринбург.
Дерябин Сергей Львович, доктор физ.-мат. наук, профессор, Уральский государственный университет путей сообщения, г. Екатеринбург.
Кульбачинский Владимир Анатольевич, доктор физ.-мат. наук, профессор, профессор кафедры физики низких температур и сверхпроводимости, физический факультет, Московский государственный университет им. М.В. Ломоносова, г. Москва.