В типовых экзаменационных вариантах ЕГЭ по математике под редакцией А.Л. Семенова и И.В. Ященко 2011, 2012 и 2013 гг. в открытом банке задач портала «Обучающая система Дмитрия Гущина "Решу ЕГЭ"» (С6 № 484659) приводится интересная и полезная задача С6 следующего содержания: «Бесконечная десятичная дробь устроена следующим образом. Перед десятичной запятой стоит нуль. После запятой подряд выписаны члены возрастающей последовательности натуральных чисел аn. В результате получилось рациональное число, которое выражается несократимой дробью, знаменатель которой меньше 100. Найдите наименьшее возможное значение а3» [1, с. 32].
Приведено решение: «Очевидно, а3³3, причем а3=3, только если а1=1, а2=2, то есть если дробь начинается: 0,123… (четвертая цифра не ноль). Заметим, что таким образом начинается, например, число
m=10-1+2×10-2+3×10-3+…+n×10-n+… .
Найдем число m и проверим, удовлетворяет ли оно условиям задачи. Для этого запишем сумму подробнее.
m=10-1+10-2+10-3+…+ 10-n+…+
+10-2+10-3+…+ 10-n+…+ (*)
+10-3+…+ 10-n+…+
+……….
В каждой строке – сумма геометрической прогрессии со знаменателем 10-1. Получаем:
… Число m удовлетворяет условиям задачи и … а3=3» [1, с. 166].
Представление m в виде (*) предполагает, что перенос слагаемых в сумме через бесконечное число других слагаемых (переместительный закон) и произвольная расстановка скобок (сочетательный закон) не изменяет суммы бесконечного числа слагаемых.
Известно, что применение сочетательного и переместительного законов к бесконечным суммам может привести к противоречиям. Приведем примеры. Суммой ряда, по определению, называют бесконечную сумму со «стандартной» расстановкой скобок …(…((а1+а2)+а3)+…+аn)+…, точнее, предел конечных сумм, полученных согласно указанной расстановке скобок.
Если допустить справедливость выполнения сочетательного закона, то, например, суммой ряда 
является, с одной стороны,
(–1+1)+ (–1+1)+ +(–1+1)+… = 0+0+0+…=0, а с другой стороны, –1+(1–1)+(1–1)+…= –1+0+ +0+…= –1, хотя, по определению, сумма этого ряда не существует, поскольку предел частичных сумм s1= –1, s2= –1+1=0, s3= –1+1–1= –1,… не существует.
Рассмотрим ряд
Известно, что этот ряд сходится и сумма его равна 
. Представим, переставив слагаемые, сумму в виде [2, с. 254]:
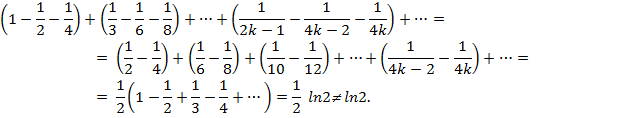
По теореме Римана из этого ряда подходящей перестановкой его членов можно получить сходящийся ряд с любой наперед заданной суммой, а также расходящийся ряд.
Вернемся к исходной задаче ЕГЭ. Полагаем, что для полноты решения, приведенного в [1], необходимо сначала доказать сходимость ряда 
, поскольку переместительный закон справедлив лишь для абсолютно сходящихся рядов, а это требует определенных знаний и навыков, хотя во введении данного сборника указано: «Задание С6 требует высокой математической культуры, но не очень много специальных знаний…».
С бесконечными суммами школьники сталкиваются при изучении суммы бесконечной геометрической прогрессии. В математических классах ученики могут знакомиться с понятием суммы числового ряда. Более тонкие вопросы, связанные со сходимостью рядов, как возможность применения переместительного и сочетательного законов, выходят далеко за рамки школьной программы. Рассуждения же по аналогии (перенос свойств с конечных сумм на бесконечные) очень часто приводят к неправильным выводам.
Есть еще один вопрос. Если задача будет решена подбором, то по каким критериям будет произведена оценка решения? Приведенные критерии не предусматривают такого варианта.
Приведем другое решение рассматриваемой задачи ЕГЭ. Естественнее начать поиск с правильных обыкновенных дробей, так как их, с заданными ограничениями на знаменатель, будет конечное число и, следовательно, возможен перебор. Если существует дробь, начинающаяся с 0,123…= m, то она меньше дроби 0,125:
Уменьшать дроби будем за счет увеличения знаменателя, оставляя числитель неизменным. Отсюда следует, что если существует дробь m, равная обыкновенной дроби со знаменателем, меньшим 100, то знаменатель ее – двузначное число и числитель не превосходит 12. Начнем поиск с обыкновенных дробей с числителем 12:
Из приведенных трех дробей нашим требованиям удовлетворяет
Дальнейший поиск прекращаем, поскольку
Второй способ уменьшения дробей достигается уменьшением числителя с сохранением знаменателя, но среди дробей
расположенных в порядке возрастания, нет искомых.
Таким образом, условию задачи с 
удовлетворяют дроби:
Желаем выпускникам больших успехов на экзамене в поисках своих решений.
Рецензенты:
Капустина Т.В., д.п.н., к.ф.-м.н., профессор кафедры математического анализа, алгебры и геометрии Елабужского института (филиала) Казанского (Приволжского) федерального университета, г. Елабуга.
Зайниев Р.М., д.п.н., к.ф.-м.н., профессор кафедры математики Набережно-Челнинского института Казанского федерального университета, г. Набережные Челны.