Введение
При вылете плазменной субстанции из ствола коаксиального магнитоплазменного ускорителя перед ее головной частью образуется отсоединенная ударная волна [6]. Произведем оценку термодинамических параметров за ударной волной. Для этого примем некоторые упрощения – субстанцию условно будем называть затупленным телом или поршнем, расчет будем производить в одномерном случае. Если перейти к системе координат связанной с поршнем, то невозмущенный газ-воздух будет двигаться на поршень со скоростью поршня. При моделировании движения газовой волны на твердую преграду данную модель можно представить как движение двух одинаковых волн на встречу друг другу [3-5].
Методика
Для решения одномерной нестационарной газодинамической задачи будем использовать уравнения сохранения массы, импульса и энергии, записанные в дивергентной форме:
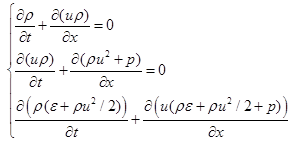. (1)
Здесь ρ – плотность газа; p – давление газа; u – скорость распространения газа; ε – внутренняя энергия газа; t,x – время и координата.
Те же уравнения (1), записанные в векторной форме, удобной для численной реализации:
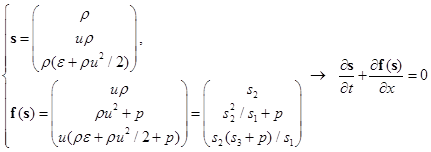, (2)
где s – вектор консервативных переменных; f(s) – вектор потока.
Описание алгоритма:
1. Замена дифференциальных уравнений в частных производных конечными разностями (2).
2. Добавление оптимального параметра регуляризации – искусственной вязкости в среде MathCAD.
3. Выбор оптимальной искусственной вязкости, используя точное известное решение (задача Сода), рис. 1, б.
4. Апробация разработанного алгоритма расчета термодинамических параметров в точке торможения (аналитически), табл.
5. Расчет динамики изменения термодинамических параметров перед плазменным поршнем при вылете из ускорителя, рис. 5.
Для численного решения системы уравнений использовался модифицированный алгоритм Лакса–Уэндроффа [1], который заключается в том, что уравнения в частных производных заменяются конечными разностями. В конечных разностях появляется неустойчивость, т.е. влияние высокочастотных шумов из-за наличия сильных ударных волн. К данному алгоритму нами была добавлена искусственная вязкость. В режиме on-line был подобран оптимальный параметр регуляризации (искусственной вязкости) для обеспечения регуляризации решения и подавления его шумовой составляющей. Формируется массив значений для каждого слоя, используя среду MathCAD:
,
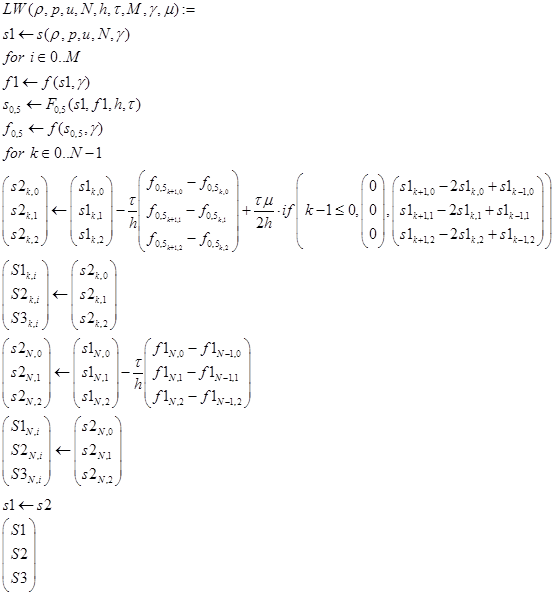где LW – функция Лакса–Уэндроффа; N=200, M=200 – число точек разбиения пространственного и временного интервалов соответственно, h, τ – шаг по пространству и времени соответственно, γ=5/3 – показатель политропы, µ – искусственная вязкость, s, f – вспомогательные функции для формирования массива значений.
Величина искусственной вязкости определялась из невязки-рассогласования (рис. 1, а). Точное известное решение задачи Сода сравнивалось с нашим алгоритмом, если рассогласования составляли не более 10 %, то коэффициент регуляризации (искусственная вязкость) считался оптимальным, рис. 1, б.
Экспериментальная часть
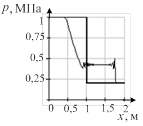
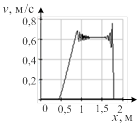
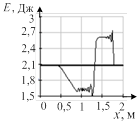
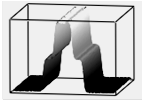
Результат расчета динамики изменения термодинамических параметров в относительных единицах приведен на рис. 2. До столкновения волн величины давления, плотности и температуры в средах были одинаковы, а скорости волн одинаковые по величине, но разные по направлению (знаку). На рисунке приведен момент времени после столкновения двух ударных волн при числе Маха, равном 1,5. Осью симметрии рисунков является фронт плазменного поршня.
Проверка работы алгоритма была проведена на расчете критических параметров – давления, плотности и температуры торможения pТ, ρТ, TТ при заданных начальных данных невозмущенного газа p0=1/γ, ρ0=1, T0=1 (в относительных единицах) и заданном числе Маха M0, рис. 4, а. Параметры торможения вычислялись по известным соотношениям [2, 8]. Давление, плотность и температура из невозмущенной среды, через скачок уплотнения, пересчитываются через ударную адиабату Гюгонио-Ренкина (ударная волна):
, 
,
.
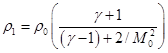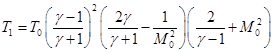а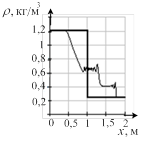
б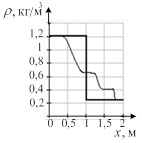
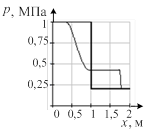
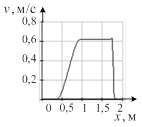
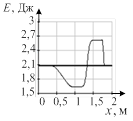
Рис. 1. Восстановленные термодинамические параметры ударной волны и волны разряжения: а) с неоптимальной вязкостью µ=10–7; б) с оптимальной вязкостью µ=10–6
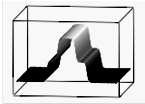
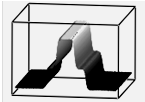
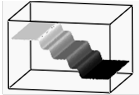
а б в г
Рис. 2. Случай двух ударных волн: а) плотность ρ; б) давление p; в) скорость v; г) энергия E
а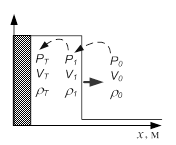
б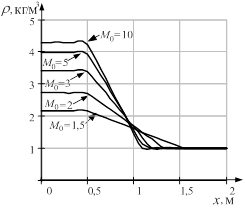
Рис. 3. Параметры ударной волны: а) критические параметры; б) распределение плотности на фронте волны при различных числах Маха M0
В нашем случае эти формулы вырождаются в простые удобные для инженерных расчетов соотношения: 
, 
, 
.
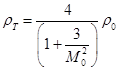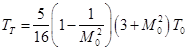Для расчета параметров торможения нужно использовать адиабату Пуассона (волна разрежения):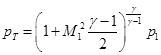 
, 
, 
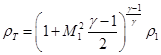, здесь M1 – числа Маха после ударной волны, определяется через число Маха в невозмущенной среде выражением: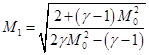
. Для инженерных расчетов получаем:
, 
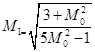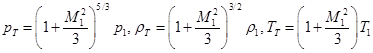. (3)
Начальные данные приведем к относительным единицам p0=1/γ=0,6, ρ0=1, T0=1.
Результаты сравнения методов сведем в таблицу.
Таблица. Результаты сравнения инженерного (И) и программного (П) расчетов
|
Число Маха M0 |
|
|
|
|
|
|
Расчет |
|
1,5 |
1,536 |
2,280 |
1,714 |
2,172 |
1,495 |
1,750 |
И |
|
1,542 |
2,287 |
1,717 |
2,175 |
1,497 |
1,752 |
П |
|
|
2 |
2,850 |
3,807 |
2,286 |
2,719 |
2,078 |
2,333 |
И |
|
2,914 |
3,893 |
2,306 |
2,744 |
2,106 |
2,364 |
П |
|
|
3 |
6,600 |
8,204 |
3,000 |
3,418 |
3,667 |
4,000 |
И |
|
6,557 |
8,151 |
2,995 |
3,413 |
3,649 |
3,980 |
П |
|
|
5 |
18,600 |
22,300 |
3,571 |
3,982 |
8,680 |
9,333 |
И |
|
18,522 |
22,206 |
3,570 |
3,980 |
8,647 |
9,298 |
П |
|
|
10 |
74,850 |
88,397 |
3,883 |
4,291 |
32,123 |
34,333 |
И |
|
75,050 |
88,643 |
3,884 |
4,291 |
32,210 |
34,426 |
П |
Приведем расстояние между ударной волной и торцом поршня S, используя формулу Лунева. Выпишем коэффициент в выражении (3):
, 
.
Как видно из табличных данных, программа дает хорошие результаты. Графическое изображение скачков уплотнения приведены на рис. 3, б. Торец поршня находится в точке x=0,5 [7]. С помощью численной схемы Лакса–Уэндроффа и введенной искусственной вязкости рассчитаем давление, плотность и температуру среды непосредственно перед поршнем по значениям скорости ударной волны, полученным из эксперимента. Экспериментальные значения координаты ударной волны L(t) (субстанции) и скорости v(t) приведены на рис. 4, а. На этом же рисунке приведены значения L(t) аппроксимированные сплайнами и сглаженные с помощью фильтра «скользящее среднее» и кривая скорости v(t), полученная взятием производной от сплайновой кривой, рис. 4, б.
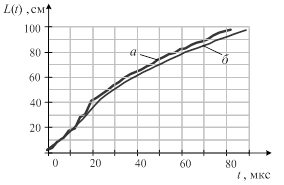
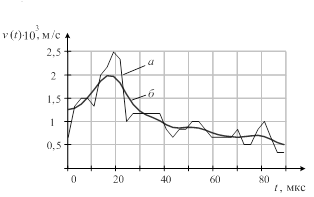
Рис. 4. Значения координаты L(t) и скорости ударной волны v(t) соответственно: а) экспериментальные значения; б) сглаженные значения
При расчете термодинамических параметров невозмущенная среда считалась одноатомным газом: постоянная политропы – 
, давление – p1=105 Па, плотность воздуха – ρ1=1,2 кг/м3, температура воздуха t=15 °C, T1=273,15+15=288,15 K, скорость звука в невозмущенной среде – c=340 м/с. На графиках приведена динамика изменения термодинамических параметров скорости ударной волны, давления, плотности и температуры, непосредственно перед плазменным поршнем, рис. 5.
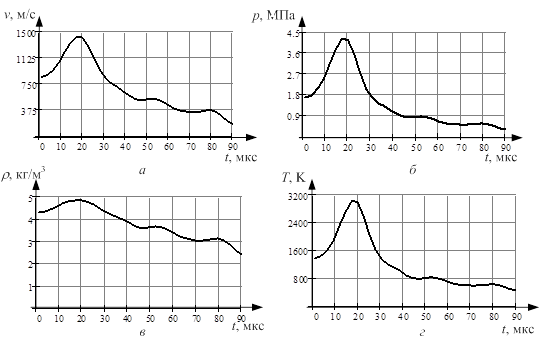
Рис. 5. Динамика изменения термодинамических параметров: а) скорость ударной волны; б) давление; в) плотность; г) температура
Прокомментируем полученный результат. При вылете плазмы из электрода-ствола со сверхзвуковой скоростью при температуре 1300…3000 К плазма представляет собой газ, распространяющийся в виде струи, которая называется недорасширенной струей. Теория позывает, что при вылете газа из сопла Лаваля [1] со сверхзвуковой скоростью первоначально газ ускоряется, а затем замедляется. Этот процесс периодически повторяется, но уже с меньшей интенсивностью. Что и наблюдается на графике (рис. 4, рис. 5, а).
Результаты
На основе модифицированного алгоритма Лакса–Уэндроффа с введением искусственной вязкости плазмы проведено моделирование параметров плазменного поршня на фронте ударной волны коаксиального магнитоплазменного устройства.
При моделировании учтены подавляющие неустойчивые высокочастотные колебания, что позволяет сузить область неоднородности и выделить только гладкие решения. Результаты расчета газодинамических параметров в точке торможения совпадают с литературными данными.
Рецензенты:
Канев Ф.Ю., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.