Введение
Повышение конкурентоспособности канатных экскаваторов связано, прежде всего, с повышением производительности за счет сохранения на всех участках рабочей траектории объема зачерпнутого грунта. Разработана конструкция рабочего органа, обеспечивающего полное наполнение ковша в процессе копания и сохранения этого объема на участках погрузки посредством соответствующего поворота ковша относительно рукояти. Кинематическое исследование предложенного механизма приведено в работе [8].
Цель исследования
Практическая реализация рабочего органа обуславливает проведение не только кинематического, но и динамического исследования процесса копания с использованием методов математического моделирования, что является основой для разработки научных основ расчета и выбора их рациональных параметров.
Предлагаемое рабочее оборудование является многоэлементным (многомассовым) и включает наряду с приводом стрелу и рукоять, на нижней части которой шарнирно закреплен ковш и два гидроцилиндра (без привода). Полости каждого из гидроцилиндров соединены между собой через гидрораспределитель, что позволяет использовать их в качестве тяг (кинематических звеньев) переменной длины. За счет введения этой дополнительной, в виде гидроцилиндров изменяемой длины, кинематической связи ковша с рукоятью (посредством одного из них) и (или) стрелой (посредством другого) реализуются усилия, обеспечивающие дополнительный поворот ковша относительно рукояти. Схема рабочего оборудования показана на рис. 1 [8].
Наиболее сложной и энергоемкой операцией, совершаемой исследуемым одноковшовым экскаватором, с точки зрения формирования внешних и внутренних нагрузок является процесс копания, вследствие чего задача по описанию его работы именно в этом режиме становится весьма актуальной.
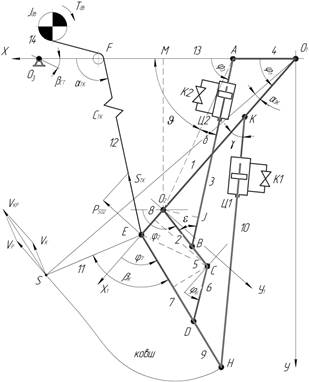
Рис. 1. Схема рабочего оборудования
На начальном этапе разработки математической модели необходимо осуществить переход от реальной конструкции к соответствующей расчетной схеме, для чего надлежит разработать некоторые допущения и методы упрощения механической системы.
В фундаментальной работе Д.П. Волкова [1] доказывается возможность значительного упрощения многомассовых эквивалентных схем при исследовании динамических нагрузок в элементах металлоконструкций и приводах одноковшовых экскаваторов. Показано, что с достаточной для практических расчетов погрешностью их можно свести до двух-трех массовых. Этот вывод многократно подтвержден, в том числе и современными исследованиями. Например, в работах [4; 10] при решении задач динамики на двух массовых схемах механизмов подъема и напора канатных экскаваторов погрешность результатов не превысила 12%.
Принимаем следующие допущения.
1. Рассматривается наиболее значимая в свете исследуемого вопроса часть траектории процесса копания, на которой осуществляется поворот рукояти относительно стрелы с одновременным поворотом ковша относительно рукояти. Нагрузка от сопротивления грунта копанию приложена к центру режущей кромки ковша.
2. Потери кинетической и потенциальной энергий учитываются механическими КПД передач и коэффициентами диссипативных потерь.
3. Разрабатываемый объем грунта условно разделен по вертикали на некоторое количество слоев с однородными, принадлежащими данному слою, свойствами по длине.
4. Эпюры напряжений и скоростей деформаций грунтовой среды в зоне действия ковша экскаватора заменяются некоторым силовым полем, которое строится по эмпирическим зависимостям типа формулы Н.Г. Домбровского – В.П. Горячкина.
5. Рабочая жидкость в гидроцилиндрах несжимаема, температура её, вязкость и плотность постоянны, утечки отсутствуют.
Правомерность подобных допущений, не искажающих физической сущности рабочих процессов землеройных машин, доказана многочисленными исследованиями, например [1; 3; 5] и др.
В соответствии с известными положениями динамики машин [5] и принятыми допущениями динамическая система рабочего органа реального экскаватора заменена эквивалентной в энергетическом отношении моделью, которая состоит из ряда сосредоточенных масс с безынерционными упругими связями. Разработанная эквивалентная схема рабочего оборудования показана на рисунке 2.
В динамической схеме к главным параметрам отнесены: массы – m; жесткости – c (податливости) упругих элементов; моменты инерции вращающихся масс – J, диссипативные коэффициенты гидроцилиндров – μ. Для этих параметров в качестве звена приведения выбран вал двигателя экскаватора.
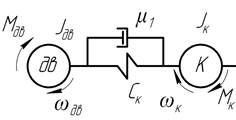
Рис. 2. Эквивалентная схема
Обобщенными координатами, определяющими положение рассматриваемой системы во времени, являются угловые перемещения: φдв – вала двигателя и φк – ковша.
Уравнение движения для каждой обобщенной координаты q можно получить через преобразование Лагранжа к уравнению энергетического баланса системы 
[5]:
, (1)
где Т – кинетическая энергия; D – диссипативная функция; П – потенциальная энергия;
W – работа внешних сил, действующих на систему; qi – обобщенная координата.
Результатом решения уравнения Лагранжа (1) для приведенной эквивалентной схемы является система уравнений:
. (2)
В уравнения (2) входят: 
, 
– крутящий момент на валу двигателя и приведенный момент сопротивления повороту ковша (с учетом поворота рукояти); с – приведенная жесткость тягового каната; 
– диссипативные коэффициенты соответствующих гидроцилиндров; 
– угол, определяющий положение передней кромки ковша (рис. 1); 
, 
– динамические моменты инерции двигателя (с учетом моментов инерции привода и барабана) и приведенный ковша (с учетом маховых масс рукояти и ковша с грузом).
Принимая во внимание, что произведение диссипативных коэффициентов на разность обобщенных скоростей двигателя 
и ковша 
, по сути, является дополнительным моментом сопротивления повороту ковша от потерь на трение по длине трубопроводов и на преодоление местных сопротивлений в соответствующих гидроцилиндрах Цi, следовательно, это произведение можно заменить на выражение [2]
, (3)
где 
– дополнительные моменты сопротивления от перемещения жидкости в гидроцилиндрах, соответственно Ц1 или Ц2 (рис. 1); 
– потери давления в гидроцилиндрах; 
– рабочая площадь гидроцилиндров; 
– плечо силы на штоке гидроцилиндров относительно точки поворота рукояти.
С учетом формулы (3) и вышеизложенного перепишем уравнения (2) в виде
(3)
где i – передаточное отношение привода барабана; а – кратность полиспастной системы.
Приведенный момент сопротивления
, (4)
где 
– момент от силы копания 
; 
– момент от сил тяжести ковша 
и грунта в ковше 
.
Согласно методике Н.Г. Домбровского [6], в методическом плане полностью идентичной методике В.П. Горячкина, результирующая сила сопротивления копанию определяется в функции от удельного сопротивления копанию 
и площади поперечного сечения стружки 
то есть
, (5)
где 
– ширина резания, равная ширине ковша; 
– толщина стружки.
Значения , которые приводятся в [6], определены в результате многочисленных экспериментальных исследований процесса копания грунтов различных по трудности разработки категорий от I до VIII экскаваторными ковшами различных геометрических параметров. Полученные значения удельных сопротивлений учитывают все внешние и внутренние силы трения, возникающие при копании и наполнении ковша грунтом, что, по сути, отражает влияние всех трех членов формулы В.П. Горячкина. Условием значимых значений является максимальное заполнение объема ковша при максимально возможной площади поперечного сечения стружки. Установлены и ограничения: ширина ковша должна быть более 0,4 м, а диапазон значений толщины стружки может находиться в пределах 0,1…0,33 ширины ковша.
Известны многочисленные попытки уточнения этой формулы путем учета физико-механических свойств грунта и материала ковша, влияния боковых стенок, углов резания и затупления зубьев и др. параметров, однако формула Н.Г. Домбровского является наиболее приемлемой для описания динамики процессов копания одноковшовым экскаватором.
Несмотря на различные подходы, общим для всех методов определения усилий копания является вывод, что определяющим параметром следует считать толщину стружки, наибольшее значение которой находится из условий максимального усилия в тяговом (подъемном) канате и устойчивости экскаватора.
Наиболее благоприятными режимом работы приводов рабочего оборудования с точки зрения динамики является работа по такой дуге копания, которая обеспечивает равномерный по толщине срез стружки [1; 6]. Этот вывод справедлив при копании по большому радиусу (рукоятью с неподвижным ковшом или с одновременным поворотом рукояти и ковша) и не относится к случаям копания только поворотом ковша [7; 9].
Применительно к рассматриваемой схеме величина определяется исходя из следующих соображений:
- заполнение объема ковша q грунтом происходит равномерно по всей длине дуги копания (траектории передней кромки ковша)
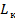, определяемой угловой координатой 
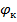и радиусом копания 
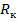; - полный угол копания 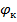складывается из двух симметричных относительно вертикальной оси частей;
- на первой части траектории
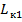копание осуществляется поворотом рукояти, а на второй 
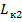одновременным совместным поворотом рукояти и ковша.
На первой части траектории копание происходит по дуге окружности радиуса 
, где 
– радиус рукояти; 
– радиус передней кромки ковша. Длина дуги при этом равна
, (6)
а на второй части траектории длина дуги описывается выражением [12]
, (7)
где 
– полярный радиус. Для рассматриваемого случая (рис. 1) определяется из треугольника SEO1 по теореме косинусов
, (8)
где 
– угол, задаваемый геометрией ковша; 
– угол поворота ковша относительно рукояти (рис. 1).
Проведенные расчеты показывают, что при заданных параметрах копания длины дуг и отличаются на малую величину, примерно на 2…4%. Это дает основание не использовать трудно решаемое выражение (7) и считать что длины дуг одинаковы. Это допущение приводит к следующему выражению для определения толщины стружки:
, (9)
где 
– коэффициент максимального наполнения ковша.
Момент от сил копания равен
. (10)
Момент от сил тяжести ковша и грунта в ковше
, (11)
где 
– масса грунта в ковше; 
– собственная масса ковша; 
– радиус центра масс ковша; 
– угловая координата радиуса .
В процессе копания масса увеличивается. Это изменение в соответствии с принятым предположением о равномерном заполнении ковша по дуге копания можно выразить зависимостью
если 
если 
(12)
где 
, 
– угловые координаты дуги копания.
Для решения задач динамики в виде уравнений (2) необходимо определиться с аналитическим описанием функции крутящего момента двигателя 
. Известны различные методы описания механической характеристики двигателя внутреннего сгорания землеройных машин. Принимаем универсальную формулу [3], где нелинейная функциональная зависимость крутящего момента на валу двигателя внутреннего сгорания 
находится по эмпирической зависимости вида
, (13)
где 
– номинальный момент; 
, 
– текущая и номинальная частоты вращения.
Входящие в формулы (2…12) кинематические и геометрические параметры механизма поворота определяются по выражениям из [8].
Заключение
Разработанная математическая модель прошла проверку и может быть использована для решения задач по оптимизации параметров механизма поворота ковша канатного экскаватора.
Рецензенты:
Хальфин М.Н., д.т.н., профессор кафедры «Подъемно-транспортные, строительные и дорожные машины» Южно-Российского государственного политехнического университета имени М.И. Платова, г.Новочеркасск.
Дьяченко А.Д., д.т.н., профессор, заведующий кафедрой «Сервис транспортных и технологических машин» Новочеркасской государственной мелиоративной академии, г.Новочеркасск.