В России прикладное математическое моделирование как дисциплина сформировалось в XX веке в трудах таких отечественных математиков, как академики М.В. Келдыш, А.Н. Тихонов, А.А. Самарский, А.А. Дородницын, Н.Н. Моисеев, Г.И. Марчук, А.А. Петров. В чём преимущество математического моделирования перед другими методами познания - эмпирическим и теоретическим?
Поскольку суть математической модели в замене оригинала на его заместителя - компьютерный образ, то это позволяет изучать не сам объект (что бывает, в частности, в эмпирических методах или очень дорого, или опасно, или неэтично), а его упрощённый образ. И поскольку моделирование состоит не только из построения компьютерного образа, но и из проведения с ним вычислительного эксперимента, то это даёт неоценимое преимущество перед мысленным экспериментом теоретического метода в проведении многих серий с богатой комбинаторикой начальных и граничных условий стартов компьютерных вычислений.
Математическое моделирование в экологии актуально ещё и по той причине, кроме вышеназванных, которую можно определить невозможностью изучать online многие экологические ситуации, т.е. в реальном масштабе времени, не только из-за того, что он может измеряться не годами и даже не десятилетиями, а веками и тысячелетиями, т.е. из-за резкого различия масштабов времени. Но, прежде всего, из-за многократного превышения природных сил над уровнем мощности технических средств современной цивилизации. Так, человеку и сейчас, кроме как в модельном мире, не по силам обуздать такое катастрофическое явление, как, например, смерч. Также математическая модель полезна и тем, что цепь событий может прокручиваться, как в кино, либо в обратном порядке, либо ускоренным образом.
В конце 60-х гг. прошлого века все громче звучали голоса, предупреждающие об угрожающих явлениях и тенденциях, которые получают планетарный масштаб и могут иметь необратимые последствия для судеб всего человечества. В докладе Римскому клубу, опубликованном в 1972 году (авторы Донелла Медоуз, Денниc Медоуз, Йорген Рандерс и Уильям Беренс), были доложены результаты моделирования роста человеческой популяции и исчерпания природных ресурсов планеты [1]. Мировая модель была построена специально для исследования пяти основных глобальных процессов:
- быстрой индустриализации;
- роста численности населения;
- увеличивающейся нехватки продуктов питания;
- истощения запасов невозобновимых ресурсов;
- деградации природной среды.
Построенная авторами доклада модель достаточно разработана, чтобы принести пользу людям, принимающим решения. Кроме того, основные тенденции, проявившиеся в поведении модели, имеют фундаментальный и общий характер, в частности:
1) если современные тенденции роста численности населения, индустриализации, загрязнения природной среды, производства продовольствия и истощения ресурсов будут продолжаться, в течение XXI века мир подойдет к пределам роста. В результате, скорее всего, произойдет неожиданный и неконтролируемый спад численности населения и резко снизится объем производства;
2) можно изменить тенденции роста и прийти к устойчивой в долгосрочной перспективе экономической и экологической стабильности. Состояние глобального равновесия можно установить на уровне, который позволяет удовлетворить основные материальные нужды каждого человека и дает каждому человеку равные возможности реализации личного потенциала.
Если народы мира выберут не первый, а второй путь, то чем раньше они начнут работать, чтобы вступить на него, тем больше у них шансов на успех.
Все составляющие доклада - численность населения, производство продовольствия, загрязнение природной среды, расход невозобновимых ресурсов - растут. Каждый год они увеличиваются по закону экспоненциального роста. Экспоненциальный рост величины означает, что за фиксированный период времени она увеличивается в фиксированное число раз.
Экспоненциальный рост - обычный процесс в биологических, финансовых и многих других системах. Экспоненциальный рост - явление динамическое. Значит, величины в этом процессе изменяются со временем. Когда множество различий величин в системе растет одновременно, и все они находятся в сложной взаимосвязи, анализ причин роста и будущего поведения системы становится очень сложным.
На протяжении 30 лет в Массачусетском технологическом институте разрабатывался новый метод динамического изучения сложных систем – метод системной динамики. В его основе лежит утверждение, что поведение системы часто зависит как от ее структуры - множества замкнутых, взаимосвязанных, нередко запаздывающих взаимодействий между составляющими элементами - так и от самих элементов. Модель мира, описанная в исследовании, построена по принципам системной динамики.
Экстраполяция существующих тенденций - проверенный временем способ заглянуть в будущее (особенно в ближайшее и особенно, если на рассматриваемые величины не слишком влияют другие тенденции, наблюдаемые в системе). Конечно, ни один из пяти исследуемых факторов нельзя назвать независимым. Каждый постоянно взаимодействует с остальными. Например, численность населения не может увеличиваться, если нет продуктов питания, производство продуктов питания растет с ростом капитала, рост капитала требует ресурсов, отработанные ресурсы увеличивают загрязнение, загрязнение среды влияет на рост численности населения и производство продовольствия. Кроме того, каждый из этих факторов через длительное время начинает испытывать воздействие обратных связей.
Учитывая реальный уровень математической подготовленности современных студентов, целью математического моделирования в экологии полагаем на первом этапе освоения основ моделирования формирование начальных навыков последовательного построения качественной дискретной модели для изучения динамики разнообразных экологических ситуаций.
Эколого-экономическая система с позиций системного подхода представима в виде конечного набора факторов - элементов, находящихся во взаимодействии друг с другом. В современном моделировании такое взаимодействие записывается с помощью когнитивной карты, которая представляет собой знаковый взвешенный ориентированный граф (орграф). Знак на дугах, ориентированных рёбрах графа, показывает характер воздействия одних факторов, расположенных в вершинах графа, на другие: «+» означает увеличение значения величины показателя фактора в вершине, куда входит дуга; «-» - уменьшение величины этого показателя в аналогичной ситуации с входящей дугой. Кроме знака, на дуге орграфа указывается её вес, т.е. коэффициент, характеризующий усиление воздействия, если он больше 1, или ослабление воздействия одного фактора на другой, если этот коэффициент меньше 1.
В минимальный набор начальных сведений по построению качественных математических моделей входит понятие обратной связи. Согласно теореме Маруямы [2; 3] обратная связь будет положительной, если все дуги контура обратной связи с положительным знаком или число отрицательных знаков на контуре – чётное; аналогично, обратная связь будет отрицательной, если количество отрицательных знаков нечётное число. Итоговый баланс, т.е. сумма контуров положительной обратной связи с учётов веса дуг и взвешивания по длине контура, сравнённая с суммой контуров отрицательной обратной связи с аналогичным учётом весов, позволяет приближённо оценить тип обратной связи в построенной модели, приводящий к неограниченному росту показателей, т.е. к неустойчивости, или ведущий к устойчивому равновесному состоянию.
В качестве примера, иллюстрирующего применение описанного математического аппарата к анализу экологической ситуации в промышленной зоне крупного города, приведём знаковый ориентированный граф из учебно-методического пособия [4] (рис. 1).
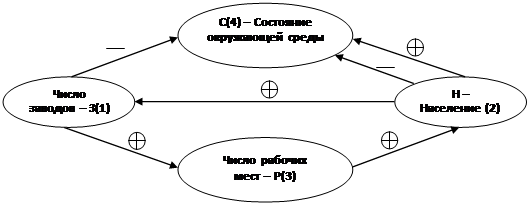
Рис. 1. Знаковый ориентированный граф
В простейшей модели, представленной на графе, легко прочитывается отрицательная обратная связь, стабилизирующая экологическую ситуацию: рост числа заводов – З(1) негативно (знак минус на дуге) влияет на состояние окружающей среды – С(4); пропорционально её ухудшению идёт уменьшение численности населения города – Н(2); уменьшение численности населения Н(2) ведёт к банкротству и закрытию части заводов – З(1); это уменьшение, поскольку дуга З(1) - С(4) несёт на себе отрицательный знак, приводит к улучшению экологической ситуации, а далее цикл повторяется. Примеры подобного применения знаковых ориентированных графов, более сложные по характеру и решающие прикладные эколого-экономические проблемы, содержатся в списке литературы [1-3]. Освоение учащимися обозначенной математической технологии позволит сделать соответствующие разделы дипломных работ более эффективными и ориентированными на современные перспективы развития экономики и системы общественного воспроизводства.
Опыт обучения студентов по дисциплинам «Социальное прогнозирование и проектирование», «Математическое моделирование социальных процессов», «Математические модели в гуманитарных науках» показал, что наиболее целесообразно начинать эти дисциплины с именно с когнитивного моделирования на ориентированных графах [4; 5]. Именно элементарная топология позволяет содержательное описание процесса или явления представить через набор взаимодействующих факторов, а затем двигаться в направлении построения дискретной системы рекуррентных уравнений, описывающих динамику процесса или изменений явления. При наличии подходящих условий и соответствующих эмпирических референтов эта система может преобразоваться или в конечно-разностные уравнения - КРУ, или в систему обыкновенных дифференциальных уравнений - ОДУ.
Рецензенты:
Губонина З.И., д.т.н, профессор, МГОУ, г. Москва.
Русак О.Н., д.т.н., профессор, МАНЭБ, г. Санкт-Петербург.
Лукьянова М.И., д.п.н., доцент, зав. кафедрой педагогики и психологии, Ульяновский институт повышения квалификации и переподготовки работников образования, г.Ульяновск.



