Точность формы и размеров прямошовных сварных труб большого диаметра (до 1420 мм) главным образом определяется минимальными их отклонениями от цилиндричности на стадии прессовой формовки. При формовке труб большого диаметра возникают искажения геометрии заготовок из-за пружинения, технологии изготовления (ребристость при пошаговой формовке) и др. Для установления влияния особенностей процесса формовки на качество изделий требуется получение расчетной модели, учитывающей параметры исходной заготовки и оборудования [6].
Наиболее производительным способом формообразования таких изделий из листовой заготовки является так называемый UOE-процесс [5]. Он включает три последовательные стадии (перехода) деформации: стадию предварительной подгибки кромок, стадию предварительной формовки u-образной заготовки и заключительную стадию.
Изготовление труб высокой точности требует получения минимальных отклонений от номинальных размеров на каждом из этих переходов. Ниже рассматривается вторая стадия предварительной формовки, для которой важно определить геометрию формующего инструмента и параметров настройки прессового оборудования с учетом конкретных механических свойств деформируемого металла, существенно влияющих на остаточные деформации (пружинение) получаемого изделия.
Одним из главных геометрических показателей изделий на стадии предварительной формовки является размер хорды a-a1 (рис. 1), который, в частности, определяет возможность размещения и позиционирования заготовки в технологическом инструменте пресса окончательной формовки и в конечном счете - геометрическую точность трубной заготовки под сварку.
а 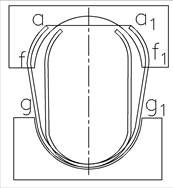 б
б 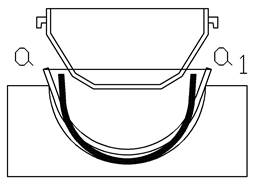
Рис. 1. Схема предварительной формовки труб: а – одношовной, б – двухшовной
Основными характеристиками, определяющими размер распружинивания a-a1, являются механические свойства материала изделия, соотношение его толщины стенки с радиусами технологического инструмента и начальная ширина исходного листа с учетом его необходимых последующих деформаций. С этой целью для стадии предварительной формовки нами разработан программный комплекс, позволяющий в диалоговом режиме выполнять расчет «пружинения» заготовки с учетом многовариантности вышеназванных факторов. В основу комплекса положены нижеследующие зависимости.
Угол пружинения определяется по формуле [3]:
![]() , (1)
, (1)
где: r - радиус пуансона;
s - толщина стенки;
α - угол формовки.
Радиус заготовки после снятия нагрузки может быть найден по зависимости [2]:
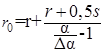 (2)
(2)
Ширина листа Bl после строжки на кромкострогальном станке определяется по зависимости [2]: для одношовной трубы ![]() (3)
(3)
и для двухшовной трубы ![]() , (4)
, (4)
где ΔP учитывает раздачу в прессе-расширителе — ΔP = 0,012…0,016;
Δf - обжатие в прессе окончательной формовки — Δf = 0,003…0,016;
ks - коэффициент, учитывающий потери металла в зоне сварки на угар, разбрызгивание и образование грата — ks = 0,4—0,5;
Δr - величина редуцирования при сварке — Δr=(8…9) мм
После подгибки кромок заготовка будет иметь вид, показанный на рис. 2.
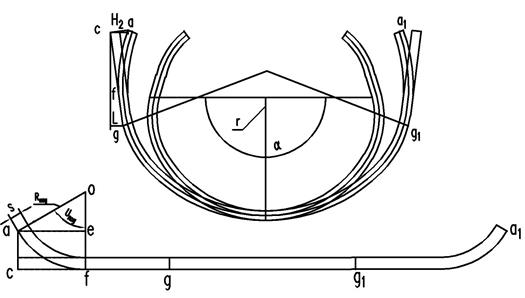
Рис. 2. Схема формовки заготовки однорадиусным пуансоном
Обозначения участков на рис. 1 соответствует обозначениям рис. 2. Длина участка gg1 находится по формуле:
gg1 = α(r+0.5S), (5)
где α - угол охвата пуансона предварительной формовки заготовкой.
Длина участка подгибки находится по формуле:
afcр=Uпод(Rпод + 0.5S), (6)
а длина участка cf будет равна:
cf= (Rпод + S)SinUпод (7)
С учетом (3)(4)(5)(6) длина участка fg будет равна:
fg=0.5(Bl - 2afcр - gg1) (8)
Угол поворота сечения g после снятия нагрузки определим по формуле (1), а радиус пружинения по формуле (2). Увеличение хорды пружинения при повороте участка cg на угол φпр= 0.5(α - Δα) будет равно:
L=2 cg Cos φпр ` (9)
Изменение хорды пружинения за счет подогнутых кромок определится по зависимости:
H2= (Rпод+S)(1 - CosUпод)Sinφпр (10)
Окончательно хорда aa1 (рис. 1) найдется по выражению:
aa1=2((R0B+S) Sinφпр) + L - 2H2 (11)
В случае двухрадиусного пуансона соответствие между участками заготовки до и после формовки показано на рис. 3.
Длины участков могут быть найдены по зависимостям:
gg1 = α1(r+0.5S), (12)
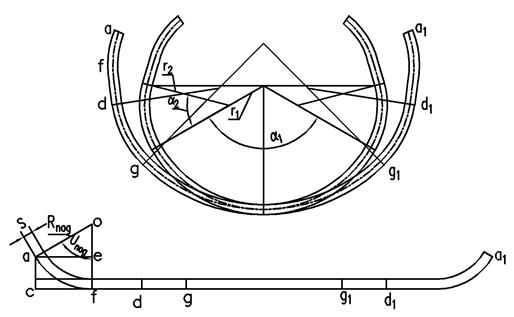
Рис. 3. Схема формовки заготовки двухрадиусным пуансоном
dg = α2(r+0.5S), (13)
fd=0.5(Bl - 2afcр - 2dg - gg1) (14)
Угол поворота сечений g и d после снятия нагрузки определим по формуле (1), а радиус пружинения участков gg1 и dg по формуле (2). Увеличение хорды пружинения при повороте участка cd на угол φпрс= 0.5(α1 – Δαс) + (α2 – Δαк) будет равно:
L=2 cd Cos φпрс, (15)
где: φпрс - суммарный угол пружинения обоих участков заготовки.
Изменение хорды пружинения за счет подогнутых кромок определится по зависимости:
H2= (Rпод+S)(1 - CosUпод)Sinφпрс (16)
Окончательно хорда aa1 (рис. 1) найдется по выражению:
aa1=2((rпр1- rпр2) Sinφпр1 + (rпр2+ S) Sinφпрс) + L - 2H2 (17)
Разработанный комплекс позволяет резко снизить трудоемкость расчетов при выборе параметров, обеспечивающих возможность окончательной формовки. Результаты расчета пружинения характерной заготовки в расчетном диалоговом окне разработанного программного комплекса приведены на рис. 4.
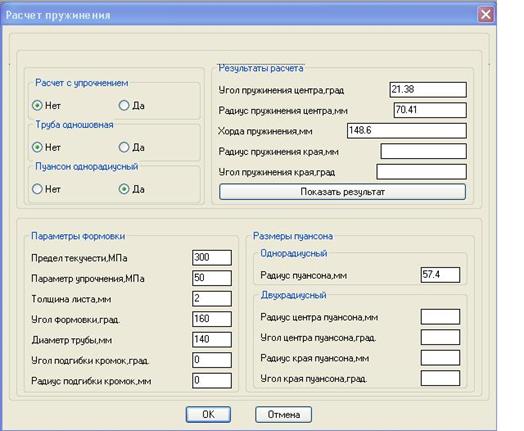
Рис. 4. Диалоговое расчетное окно программного комплекса
Для проверки расчетной методики и программного комплекса использовано сравнение с экспериментальными данными. Ввиду сложности широких испытаний на действующем оборудовании была создана физическая модель для необходимых замеров основных характеристик предварительной формовки (рис. 5).
а  б
б 
Рис. 5. Физическая модель пресса предварительной формовки:
а – общий вид установки, б – этап формовки
Для определения геометрических параметров заготовок после формовки находит свое применение обработка в «Автокаде» растровых изображений, полученных фотографированием или сканированием [4]. Обработанное в «Автокаде» изображение заготовки, полученной на установке (рис. 5), показано на рис. 6а.
а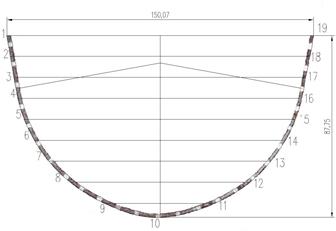 б
б 
Рис. 6. Заготовка после предварительной формовки: а – отсканированное изображение заготовки, обработанное в «Автокаде», б – схема измерения координат заготовки на КИМ
Для оценки точности использования растровых изображений можно использовать координатно-измерительные машины (рис. 6б).
Результаты замера координат точек заготовки по рис. 6 приведены в таблице 1.
Таблица 1 - Результаты замера координат точек заготовки после предварительной формовки
|
Номер точки |
«Автокад» |
КИМ |
||
|
X |
Y |
X |
Y |
|
|
1 |
0 |
0 |
0 |
0 |
|
2 |
1,71 |
10 |
1,87 |
10 |
|
3 |
3,41 |
20 |
3,75 |
20 |
|
4 |
5,46 |
30 |
5,82 |
30 |
|
5 |
8,47 |
40 |
9,01 |
40 |
|
6 |
13,25 |
50 |
14,01 |
50 |
|
7 |
20,22 |
60 |
21,19 |
60 |
|
8 |
30,40 |
70 |
31,92 |
70 |
|
9 |
46,62 |
80 |
48,81 |
80 |
|
10 |
74,54 |
87,75 |
75,08 |
86,38 |
|
11 |
101,98 |
80 |
101,63 |
80 |
|
12 |
118,28 |
70 |
118,9 |
70 |
|
13 |
128,57 |
60 |
129,49 |
60 |
|
14 |
135,44 |
50 |
136,71 |
50 |
|
15 |
140,35 |
40 |
141,57 |
40 |
|
16 |
143,36 |
30 |
144,76 |
30 |
|
17 |
145,28 |
20 |
146,84 |
20 |
|
18 |
147,23 |
10 |
148,78 |
10 |
|
19 |
150,07 |
0 |
150,53 |
0 |
Как следует из данных, приведенных в таблице 1, погрешность замеров по растровым изображениям не превышает 2% по сравнению с замерами, полученными с помощью координатно-измерительных машин.
Комплексная проверка на физической модели при варьировании в широком диапазоне основных параметров заготовки показала хорошую (в пределах 5%) сходимость значений, полученных расчетом, с результатами измерений. Это дает основания для использования полученного программного продукта для дальнейшего определения и выбора рациональных параметров технологического инструмента и настройки кинематики прессового оборудования.
Рецензенты:
Лехов О.С., д.т.н., профессор, зав. кафедрой механики Российского государственного профессионально-педагогического университета, г. Екатеринбург.
Паршин В.С., д.т.н., профессор, зав. кафедрой металлургических и роторных машин, ММИ ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.



