Введение
Практика эксплуатации информационно-управляющих систем (ИУС) в случае объектов управления с высокой ценой отказа (например, в ядерной и гидроэнергетике, ракетно-космической отрасли, системах связи и телекоммуникаций, металлургии, тяжелом машиностроении и других отраслях экономики) показывает, что значительная доля аварий и отказов технических средств обусловлены неправильными действиями операторов ИУС в нештатных ситуациях, требующих безошибочных и оперативных действий [6]. Это предопределяет необходимость рассмотрения ИУС как сложной человеко-машинной системы. Будучи ключевым звеном в этой сложной системе, человек-оператор в нештатных ситуациях обладает выраженными изменяемыми параметрами своих характеристик, что отражается на надежности ИУС в целом [7]. Поэтому задача организации мониторинга функционального состояния оператора (ФСО) в ИУС в настоящее время является актуальной.
Цель исследования
Цель исследования заключается в выделении и конкретизации содержания процедур мониторинга функционального состояния операторов информационно-управляющих систем.
Исходные предположения и допущения метода исследования
Под функциональным состоянием оператора будем понимать совокупность значений параметров психофизиологического состояния оператора (ППФСО), отражающих реакцию функциональных систем организма на внешние и внутренние воздействия различных уровней. Сущность мониторинга ФСО состоит в определении значений ППФСО и сопоставления с ними текущего ФСО с целью снижения отрицательных влияний ФСО на показатели качества функционирования ИУС. Отличительной особенностью рассматриваемых процедур мониторинга ФСО является то, что они осуществляются в штатном процессе функционирования (ПФ) ИУС. Подготовка и проведение процедур мониторинга ФСО в ПФ ИУС включает следующие этапы: формулировку целей и задач мониторинга; формирование группы подготовки и проведения процедур мониторинга; формирование согласованных групп экспертов; проведение экспертных опросов с целью получения априорной информации о характеристиках ИУС; определение критерия прекращения процедур мониторинга; планирование процедур и алгоритмов мониторинга ФСО в ПФ ИУС; осуществление процедур и алгоритмов мониторинга текущего ФСО операторов в ПФ ИУС; проведение анализа полученных данных, построение моделей ФСО в ПФ ИУС; разработку рекомендаций по воздействию на ФСО в ПФ ИУС; оценку эффективности реализованных рекомендаций, определение направлений совершенствования процедур и алгоритмов мониторинга ФСО в ПФ ИУС.
Наиболее трудоемкими и ответственными являются этапы планирования процедур и алгоритмов мониторинга ФСО и анализа полученных данных, т.к. именно эти этапы обуславливают в большей степени продолжительность мониторинга и статистическую достоверность получаемых результатов. Рассмотрим подробнее данные этапы. Планирование процедур и алгоритмов мониторинга текущего ФСО тесно связано с видом зависимости значений показателей качества функционирования (ПКФ) ИУС от ППФСО, поэтому ведущим в данном случае является этап анализа полученных данных и построения моделей ФСО человека-оператора.
Разработка модели
Необходимо построить модель зависимости ПКФ от ППФСО на основе некоторого числа измерений, проводимых в режиме реального времени при функционировании ИУС. Традиционно при исследовании искомой зависимости используются параметрические регрессионные модели вида [3]:
![]() ,
,
где ![]() – вектор независимых (предикторных) переменных, характеризующих значения показателей ППФСО;
– вектор независимых (предикторных) переменных, характеризующих значения показателей ППФСО; ![]() – вектор зависимых переменных или отклик (в случае исследования ИУС зависимыми переменными являются значения показателей качества функционирования ИУС, например, вероятность выполнения целевых задач и коэффициент готовности ИУС);
– вектор зависимых переменных или отклик (в случае исследования ИУС зависимыми переменными являются значения показателей качества функционирования ИУС, например, вероятность выполнения целевых задач и коэффициент готовности ИУС); ![]() – матрица неизвестных параметров;
– матрица неизвестных параметров; ![]() – матрица заданных линейно независимых на множестве X функций;
– матрица заданных линейно независимых на множестве X функций; ![]() – вектор случайных величин, характеризующих аддитивную помеху, воздействующую на вектор Y.
– вектор случайных величин, характеризующих аддитивную помеху, воздействующую на вектор Y.
Учитывая, что для каждого заданного значения регрессора ![]() наблюдается не одномерный, а векторный отклик
наблюдается не одномерный, а векторный отклик ![]() , то данную математическую задачу следует называть многомерной регрессией [5].
, то данную математическую задачу следует называть многомерной регрессией [5].
Однако чаще всего исследователь не в состоянии обосновать априорно вид и структуру зависимости ПКФ от ППФСО. Поэтому в данном случае целесообразно использовать непараметрические модели. Фактором, определяющим тип непараметрической модели, является принадлежность помехи e к определенному классу [2]. Анализ экспериментальных данных, полученных в результате исследований ПФ ИУС, показал, что e принадлежит к классу распределений с ограниченной дисперсией
![]() .
.
Поэтому оптимальной моделью для зависимости ПКФ ИУС от параметров ППФСО ИУС является непараметрическая оценка регрессии.
При непараметрическом оценивании регрессии наиболее часто используют так называемую оценку регрессии Надарая-Ватсона [4]:
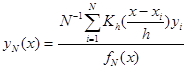 ,
,
где ![]() – непараметрическая оценка регрессии; xi, yi – соответственно наблюдаемые значения предикторной переменной и ПКФ исследуемой ИУС; N – число измерений;
– непараметрическая оценка регрессии; xi, yi – соответственно наблюдаемые значения предикторной переменной и ПКФ исследуемой ИУС; N – число измерений; ![]() – непараметрическая оценка плотности вероятности типа Розенблатта-Парзена [3]; h – ширина окна сглаживания;
– непараметрическая оценка плотности вероятности типа Розенблатта-Парзена [3]; h – ширина окна сглаживания; ![]() – ядерная функция (функция сглаживания).
– ядерная функция (функция сглаживания).
Для m-мерного случая непараметрическая оценка регрессии имеет вид
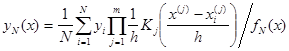 ,
,
где ![]() – j-ое значение i-ой предикторной переменной.
– j-ое значение i-ой предикторной переменной.
Качество оценки регрессии существенно зависит от неравномерности размещения точек ![]() . Для устранения этого эффекта в соответствии с [3] целесообразно использовать непараметрическое многомерное нормальное ядро, оценка которого определяется выражением
. Для устранения этого эффекта в соответствии с [3] целесообразно использовать непараметрическое многомерное нормальное ядро, оценка которого определяется выражением
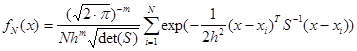 ,
,
где S – выборочная ковариационная матрица.
Особого внимания заслуживает вопрос исследования особенностей построения непараметрической оценки регрессии вблизи границ интервала наблюдения, т.к. в этом случае число наблюдений, усредняемых около границы интервала, уменьшается, и это сказывается на дисперсии или смещении. В [4] предлагается метод, позволяющий просто и эффективно решить граничную проблему (так называемый «метод складного ножа»). Показано, что непараметрическая оценка регрессии может быть представима в виде линейной комбинации ядерных оценок с шириной окна ![]()
![]() ,
,
где R и ![]() определяются видом ядра.
определяются видом ядра.
Результаты исследования и их обсуждение
Одним из требований к процедурам мониторинга является оценка достоверности полученных результатов. Для оценки регрессии оценка достоверности традиционно определяется доверительными интервалами. Обобщая теорему о максимальном абсолютном отклонении ![]() от
от ![]() , приведенную в [4], для многомерного нормального ядра можно определить вид распределения:
, приведенную в [4], для многомерного нормального ядра можно определить вид распределения:
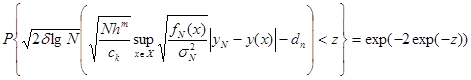 ,
,
где
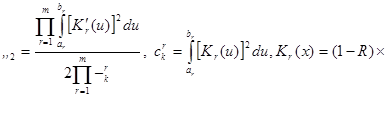
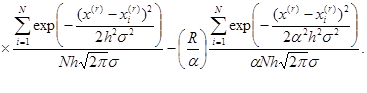
Необходимо отметить, что нецелесообразно построение оценок регрессии со значительной размерностью. Это связано с возрастанием дисперсии при увеличении размерности. Поэтому число предикторных переменных должно быть согласованно с объемом выборки. На практике приемлемой оказывается регрессия, имеющая 3-4 предикторных переменных.
Планирование процедур мониторинга реализуется с целью обеспечения максимальной достоверности оценки регрессии при заданном объеме выборки либо для обеспечения требуемой достоверности получаемых результатов при минимальном объеме выборки.
Так как для оценивания зависимости ПКФ ИУС от ППФСО используется непараметрическая оценка регрессии, то необходимо использование непараметрических методов последовательного планирования процедур и алгоритмов мониторинга. Для непараметрической оценки регрессии критерием оптимальности является g-критерий [3].
С учетом изложенного выше, непараметрическая оценка g-критерия для многомерного нормального ядра с учетом краевых эффектов определяется выражением
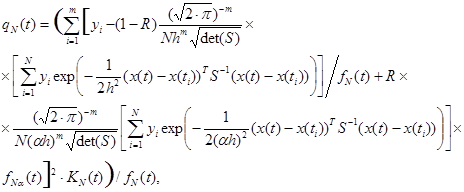
где ![]() – ядерная функция, учитывающая граничный эффект.
– ядерная функция, учитывающая граничный эффект.
Тогда оптимальный непараметрический план эксперимента определяется из решения неравенства ![]() , где C – константа, позволяющая подстраивать алгоритм планирования (увеличение константы уменьшает чувствительность алгоритма к выявлению недостаточно точных участков непараметрической оценки регрессии).
, где C – константа, позволяющая подстраивать алгоритм планирования (увеличение константы уменьшает чувствительность алгоритма к выявлению недостаточно точных участков непараметрической оценки регрессии).
Непараметрическая оценка дисперсии ![]() для многомерного нормального ядра с учетом краевых эффектов определяется статистикой
для многомерного нормального ядра с учетом краевых эффектов определяется статистикой
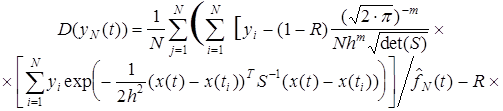
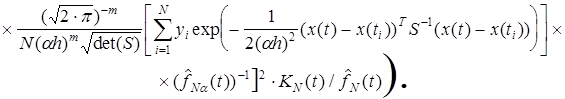
Проведенные экспериментальные исследования показали эффективность предлагаемого метода планирования и проведения процедур мониторинга ФСО. С использованием предлагаемых методов для ряда ИУС были разработаны рекомендации по коррекции ФСО, что позволило улучшить ПКФ конкретных образцов ИУС.
Выводы
Планирование процедур мониторинга текущего функционального состояния оператора тесно связано с видом зависимости значений показателей качества функционирования информационно-управляющей системы от параметров психофизиологического состояния человека-оператора. Выделены этапы анализа полученных данных и построения моделей функционального состояния человека-оператора, т.к. именно эти этапы обусловливают продолжительность мониторинга и статистическую достоверность получаемых результатов. Показано, что исследователь обычно затрудняется априорно обосновать вид и структуру зависимости показателей качества функционирования информационно-управляющей системы от параметров психофизиологического состояния оператора. В этом случае предлагается использование непараметрических моделей. Рассмотрены особенности планирования процедур мониторинга функционального состояния операторов информационно-управляющих систем. Критериями эффективности планирования являются либо максимальная достоверность оценки регрессии при заданном объеме выборки, либо требуемая достоверность при минимальном объеме выборки.
Рецензенты:
Козлов В.В., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Смагин В.А., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.



