Введение
В работах [4, 5] предложены новые виды фундаментов мелкого заложения в виде ленточных фундаментов, объединенных цилиндрическими бинарными оболочками (рис. 1).
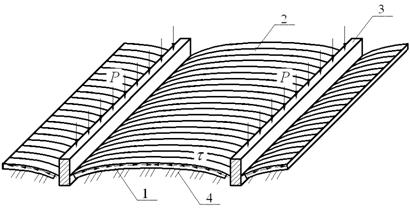
Рисунок 1. Ленточные фундаменты, объединенные цилиндрическими бинарными оболочками: 1 – оболочка; 2 – мембрана; 3 – ленточный фундамент;
4 – естественное или искусственное основание
Данные фундаменты эффективны в условиях слабых грунтов, обладающих высокой сжимаемостью, а также в условиях достаточно тонкого верхнего прочного слоя грунта, подстилаемого слабыми грунтами. В таких фундаментах мембрана работает на растяжение, а цилиндрическая оболочка испытывает совместное действие усилий растяжения и изгибающих моментов. При этом в реальных фундаментах в значительной степени реализуются силы трения на контакте «мембрана – оболочка» и «оболочка – грунт» (рис. 2), которые влияют на напряженно-деформированное состояние (НДС) системы «фундамент – грунтовое основание».
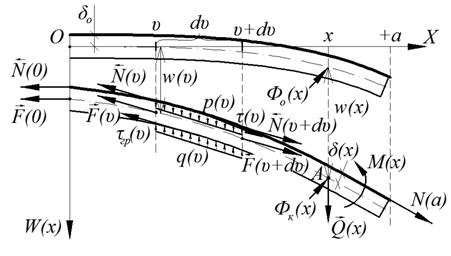
Рисунок 2. Расчетная схема для определения моментов сил при симметричном нагружении
При использовании бинарных оболочек и отсутствии трения между мембраной и оболочкой оболочка работает на изгиб, и в этом случае касательные силы трения реализуются в пределах, характерных для традиционных сплошных фундаментов с плоской подошвой, работающих на поперечный изгиб. В подавляющем числе случаев касательными силами трения при расчете плитных фундаментов пренебрегают ввиду их незначительности [1, 3]. При наличии трения между мембраной и оболочкой часть усилия растяжения будет передаваться на оболочку, что с учетом трения между оболочкой и грунтом может повлиять на НДС системы «фундамент – грунтовое основание».
Трение
между мембраной и оболочкой зависит от применяемых материалов и качества
поверхностей. Пусть 
определяет коэффициент трения между
мембраной и оболочкой, а 
– коэффициент трения между оболочкой и
грунтом, предельное значение которого ограничено прочностью грунта на сдвиг.
Обозначим
уравнение срединной линии оболочки в заданной системе координат до приложения
усилий как 
. Ее
же положение после приложения усилий как 
.
Тогда величина смещения конструкции w(x) будет равна:
.
(1)
Если предположить, что сечение оболочки не является постоянным, а задается функцией δ(x) – половина толщины оболочки в точке с координатами x, то можно восстановить вид зависимости для линии контакта мембраны и оболочки, а также оболочки и грунта.
Уравнение линии контакта «мембрана-оболочка» имеет вид:
.
(2)
Уравнение линии контакта «оболочка-грунт» имеет вид:
.
(3)
Для вывода уравнения изгиба оболочки выпишем выражения для моментов относительно точки A с координатой x, для всех сил, действующих на участке от υ до υ+dυ. Если p(υ) – давление мембраны (возможно и с присутствием внешних усилий) на бетонную оболочку на отрезке [υ, υ+dυ] с плечом x-υ, то момент этой силы равен:
.
(4)
Более
детальный анализ показывает, что в случае значительного прогиба, плечо силы 
будет
определяться расстоянием, взятым от точки A до точки приложения силы вдоль
касательной в этой точке, то есть можно записать:
, (5)
где
.
Если
предположить, что оболочка достаточно полога, тогда 
, то 
и выражение
для момента этой силы совпадает с тем, что было получено ранее.
Пусть q(υ) – давление отпора грунта на оболочку на отрезке [υ, υ+dυ] с плечом x-υ, то величина элементарного момента этой силы имеет вид:
.
(6)
Аналогично, детальный анализ, проведенный по той же схеме, дает нам:
, (7)
где
.
Момент
сил трения, возникающих за счет соприкосновения мембраны с оболочкой на отрезке
[υ, υ+dυ] определяется
величиной касательного напряжения 
и
плечом, выражение для которого можно записать в следующем виде:
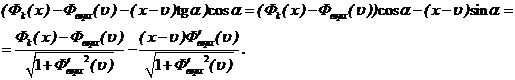(8)
После упрощения и предположения о наличии пологости оболочки, получаем:
,
.
(9)
Аналогичное
выражение для момента сил трения между оболочкой и грунтом 
с
плечом действия:
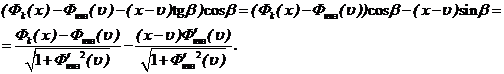(10)
Как и выше, в предположении пологости:
.
(11)
Для отыскания суммарных величин моментов вычислим интегралы по отсеченной части бинарной оболочки. Из рассмотрения баланса моментов в выделенном сечении оболочки получим искомое уравнение.
Выпишем выражения для суммарных величин моментов:
- сил, действующих нормально к поверхности практически нерастяжимой мембраны, опирающейся на бетонную оболочку и, возможно, внешних сил:
,
(12)
- сил отпора, действующих со стороны грунта на оболочку q(x):
,
(13)
- сил трения между мембраной и оболочкой τ(x):
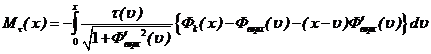, (14)
- сил трения между оболочкой и грунтом τгр(x):
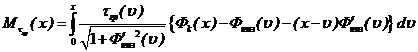. (15)
Все эти моменты компенсируются моментом, возникающим из-за наличия ненулевой изгибной жесткости оболочки:
. (16)
Уравнение баланса моментов примет вид:
.
(17)
Полученное уравнение для определения величины смещения, содержащее интегралы с переменным верхним пределом, можно упростить за счет повторного дифференцирования.
Окончательный вид уравнения деформирования пологой оболочки с учетом трениями по контакту «мембрана – оболочка» и «оболочка – грунт», имеет вид:
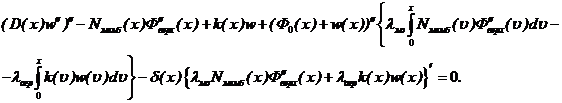(18)
Решение интегро-дифференциального уравнения деформирования бинарной оболочки в составе ленточных фундаментов на грунтовом основании (18) реализовано на языке Паскаль [6] в среде Delphi [2].
На рисунке 3 представлен интерфейс программы для расчета взаимодействия ленточных фундаментов, объединенных бинарными цилиндрическими оболочками с грунтовым (линейно-деформируемым) основанием.
Расчетом определяется осадка ленточных фундаментов и бинарных оболочек, реактивные давления под подошвой фундамента, усилие натяжения мембраны, растяжения оболочки, изгибающие моменты и поперечные силы в оболочке. Расчет производится в автоматическом режиме при вводе необходимых исходных данных по фундаменту, нагрузкам на него и свойствам грунтового основания.
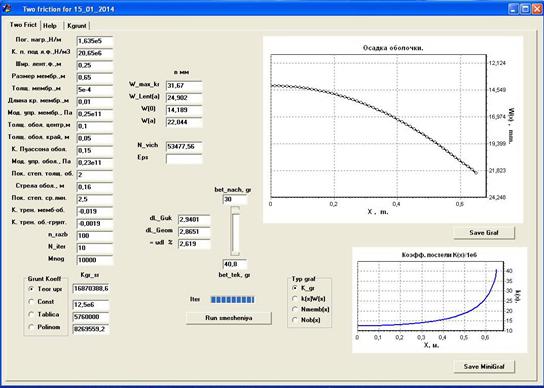
Рисунок 3. Интерфейс программы
Все искомые величины определяются на основании численного решения дифференциального уравнения (18) относительно осадки w с соответствующими граничными условиями.
На
рисунке 4 представлены зависимость осадки ленточных фундаментов от
коэффициентов трения и .
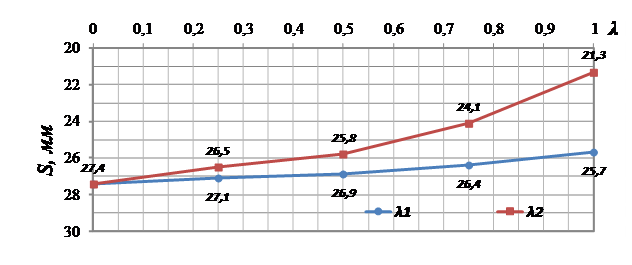
Рисунок 4. Зависимость осадки ленточных фундаментов
от коэффициентов трения и
На
рисунке 5 представлена зависимость изменения натяжения мембраны от коэффициента
трения .
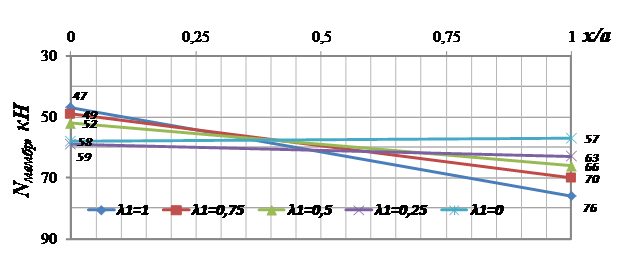
Рисунок 5. Зависимость изменения
натяжения мембраны от коэффициента трения :
x – координата точки, a – полупролет бинарной оболочки
По результатам выполненных исследований следует сделать следующие выводы:
1. Разработана расчетная схема взаимодействия ленточных фундаментов, объединенных бинарными оболочками, с грунтовым основанием, моделируемым гипотезой Винклера, с учетом сил трения на контакте «мембрана – оболочка» и «оболочка – грунт».
2. Численно реализовано аналитическое решение взаимодействия бинарных оболочек с грунтовым основанием, моделируемым гипотезой Винклера, с учетом сил трения на контакте «мембрана – оболочка» и «оболочка – грунт».
3.
В результате численного моделирования выявлено, что при геометрических размерах,
характерных для фундаментов реальных зданий и сооружений, изменение
коэффициента трения на контакте «мембрана – оболочка»
в пределах 0 <<1, влияет на изменение
осадки ленточного фундамента в пределах 6%. Изменение коэффициента трения на
контакте «оболочка – грунт» в
пределах 0 <<1 влияет на изменение осадки
ленточного фундамента в пределах 22%.
4.
При увеличении до единицы усилие растяжения
мембраны в заделке ленточного фундамента увеличивается на 33%, а в центре
уменьшается на 18% по отношению к равномерному распределению усилия растяжения,
характерного при отсутствии трения на контакте «мембрана
– оболочка», т.е.=0. λ1
Миронов В.В., д.т.н., профессор, профессор кафедры «Водоснабжение и водоотведение» ФГБОУ ВПО ТюмГАСУ, г. Тюмень.
Чекардовский М.Н., д.т.н., профессор, заведующий кафедрой «Теплогазоснабжение и вентиляция» ФГБОУ ВПО ТюмГАСУ, г. Тюмень.