Введение
При изучении курса элементарной геометрии большое значение, бесспорно, занимают задачи на построение. Трудно переоценить роль задач на построение в формировании математического мышления школьников. Однако констатирующее исследование [1-3] показало, что задачи на построение вызывают значительные трудности у школьников и студентов физико-математического факультета. Наибольшую трудность вызывают этап анализа и этап исследования в задачах такого вида. На наш взгляд, это связано с тем, что, во-первых, задачи на построение часто являются задачами повышенной трудности, так как требуют для своего решения введения дополнительных (вспомогательных) построений; во-вторых, с недостатком внимания как школьных учителей математики, так и преподавателей геометрии к задачам такого рода; в-третьих, с недостаточной разработанностью методики решения таких задач.
Некоторые вопросы методологии геометрических построений на плоскости циркулем и линейкой рассмотрены в трудах А.А. Адлера, И.И. Александрова, Г.Г. Масловой, Г.М. Олифера, Д.И. Перепелкина, Г.П. Сенникова, А.С. Смогоржевского, Н.Ф. Четверухина, С. Шатуновского, Г.Х. Воистиновой. Один из аспектов обучения решению задач на построение, в частности задач на построение практического содержания, рассмотрен нами в работах [2; 3].
Вопросы же методики обучения проведению этапа анализа и исследования в задачах на построение, введения вспомогательных линий при решении задач такого вида и многие другие вопросы, связанные с обучением решению задач на построение, до сих пор в научно-методической литературе слабо разработаны.
Таким образом, проблема обучения школьников и будущих учителей математики решению задач на построение является важной и не достаточно разработанной.
В данной статье рассматривается сущность задач на построение и методика обучения процессу поиска их решения на этапе анализа с помощью системы наводящих вопросов и разработанного правила-ориентира.
Как и в традиционной методике, задачей на построение будем считать «математическое предложение, указывающее, по каким данным, какими средствами (инструментами) и какой геометрический образ (точка, прямая, окружность, треугольник, совокупность точек и так далее) требуется найти (начертить, построить на плоскости, наметить на местности и так далее) так, чтобы этот образ удовлетворял определенным условиям» [1, с. 58].
Итак, сущность задач на построение не исчерпывается указанием данных и формулировкой того, что требуется найти. Важное значение имеет также указание на те средства, с помощью которых задача должна быть решена, на те инструменты, при помощи которых построение должно быть выполнено. В зависимости от того, какие инструменты имеются в виду, смысл одной и той же задачи коренным образом меняется.
Итак, решение задач на построение сводится к выполнению некоторых операций с помощью чертежных инструментов. Решить задачу на построение – по заданным в условии задачи элементам (точкам, прямым, окружностям и так далее) найти искомые элементы, удовлетворяющие сформулированным в условии задачи требованиям. Обычно эти требования указывают отношения, в которых должны находиться искомые элементы друг с другом или с заданными элементами.
В теории геометрических построений (в так называемой конструктивной геометрии) «инструментами» построений являются специально сформулированные (обычно в виде аксиом) соглашения, условия «конструктивности». Если для некоторого множества точек эти условия выполнены, то точки множества считаются построенными («конструктивными»). Таким образом, средства построения в строгих геометрических построениях – абстракции, а сами построения – логические операции, ссылки на те или иные аксиомы и их следствия. Можно ввести сколько угодно и каких угодно абстрактных инструментов, стоит только сформулировать соответствующую систему аксиом. Теория геометрических построений описана в работах А. Адлера, А.С. Смогоржевского, Н.Ф. Четверухина, С. Шатуновского.
Следует заметить, что не всякая задача, решенная математически, является задачей, решенной «конструктивно». Задача установления, какие элементы можно отнести к классу «конструктивных», решается с помощью аксиом инструментов.
Таким образом, решить задачу на построение с помощью тех или иных инструментов – значит свести ее к конечному числу «элементарных построений». Перечень этих элементарных построений и характеризует тот или иной комплекс инструментов.
С принципиальной точки зрения решение любой задачи на построение с помощью инструментов означает сведение ее к конечному числу элементарных операций. Однако такое сведение практически неудобно, так как делает решение более сложных задач громоздким. Чаще задачи сводятся не к самим элементарным построениям, а к типичным, часто встречающимся, задачам на построение. Эти задачи называют основными задачами на построение.
Классическая схема решения задач на построение состоит из четырех пунктов, которые принято называть этапами решения задачи на построение: анализ; построение; доказательство; исследование.
Анализ задачи – это отыскание способа ее решения, то есть составление плана: какие и в какой последовательности необходимо выполнить известные уже построения, чтобы построить искомую фигуру. Но анализ должен преследовать и вторую цель – установить полную общность найденного решения. Ошибка в анализе может приводить к потере части решения. Рассуждения в анализе проводятся по-разному, в зависимости от применяемого метода решения, но этот этап всегда должен заканчиваться формулированием плана построения.
Как уже было отмечено, цель анализа – найти искомый геометрический образ (фигуру, которую необходимо построить), используя данные в условии элементы. При этом геометрический образ может быть четырех видов: точка, прямая (отрезок), окружность, многоугольник (угол). Для построения геометрического образа достаточно построить его «узловые точки»: для прямой – любые две точки прямой; для окружности – центр и любые две точки, определяющие величину радиуса; для многоугольника – вершины многоугольника (вершина угла и любые две точки, лежащие на сторонах многоугольника) и т.п.
Итак, этап анализа является наиважнейшим этапом процесса решения задач на построение. Причем полноценный анализ должен удовлетворять нескольким требованиям:
· он должен, безусловно, позволить решить задачу, то есть должна существовать практическая возможность осуществления тех построений, которые указаны в анализе, хотя бы при некоторых соотношениях между данными в условии элементами;
· он должен быть наипростейшим из возможных способов решения данной задачи (с учетом, конечно, средств построения и запаса теоретических знаний у решающего задачу);
· он должен удовлетворять требованиям полноты, то есть должен обеспечивать все решения данной задачи, которые она вообще может иметь.
Бесспорно, что, решая задачу, уже на этапе анализа необходимо всемерно стремиться к тому, чтобы установить не какой-нибудь способ решения задачи, а наиболее полноценный, то есть удовлетворяющий трем требованиям. Однако удовлетворить этим требованиям уже на этапе анализа бывает часто трудно.
Рассмотрим методику решения задач на построение, разработанную автором.
Итак, создав на чертеже-наброске треугольники, остается выбрать из них подходящий вспомогательный треугольник и установить с его помощью способ решения задачи.
В качестве вспомогательного треугольника необходимо выбрать тот из числа созданных на чертеже-наброске треугольников, который: во-первых, содержит наибольшее число «узловых точек» искомого геометрического образа, а, во-вторых, способ построения которого наиболее простой. Соблюдая эти требования, можно будет установить наиболее простой способ решения данной задачи методом вспомогательного треугольника.
Как только выбор вспомогательного треугольника произведен, то установление с его помощью способа решения задачи обычно никаких затруднений не вызывает. Остальные точки искомого геометрического образа можно, как правило, найти, используя метод геометрических мест и данные по условию элементы.
В силу всего вышесказанного система наводящих вопросов, направляющая деятельность учащихся и студентов при проведении анализа задачи, может быть следующей.
1. Достаточно ли для проведения анализа первоначального чертежа-наброска?
2. Какому критерию допустимости геометрических преобразований соответствуют элементы, данные в условии (критерии рассмотрены в работе [1])?
3. Какой метод (методы) преобразования фигуры в силу этого критерия можно выбрать?
4. Каким образом теперь дополнить чертеж-набросок, учитывая выбранный метод преобразования?
5. Какие треугольники на чертеже-наброске образовались?
6. Какой из этих треугольников выбрать в качестве вспомогательного для решения данной задачи?
7. Как построить этот вспомогательный треугольник (вспомнить основную задачу)?
8. Сколько «узловых точек» искомой фигуры будет определено построением вспомогательного треугольника?
9. Какие «узловые точки» искомой фигуры остались неопределенными?
10. Какие элементы из числа данных в условии задачи не потребовались для построения вспомогательного треугольника?
11. Как построить остальные «узловые точки» искомой фигуры, предполагая вспомогательный треугольник построенным?
12. Все ли «узловые точки» теперь определены?
Следует отметить, что в данной статье автор приводит только обобщенную систему наводящих вопросов и обобщенное правило-ориентир. Система наводящих вопросов и правило-ориентир для каждого из классов задач на построение (основные задачи, простые задачи на построение, сложные задачи на построение, не требующие введения дополнительных линий, сложные задачи на построение, требующие введения дополнительных линий) описаны в работе [1].
Полученная система наводящих вопросов приводит к обобщенному правилу-ориентиру.
ПРАВИЛО-ОРИЕНТИР
Чтобы решить задачу на построение, необходимо:
1. Выполнить чертеж-набросок по условию задачи в предположении, что задача решена и искомая фигура построена (используя правила построения чертежа-наброска).
2. Установить, какие «узловые точки» необходимо «знать» для построения искомой фигуры (для отрезка достаточно знать два его конца, для прямой - любые две точки этой прямой, для многоугольника – все вершины этого многоугольника, для окружности - центр и любые две точки, определяющие величину радиуса этой окружности).
3. Выяснить, все ли элементы, данные в условии, изображены на чертеже-наброске. Если какие-либо элементы изображены неявно, задача требует для своего решения введения дополнительных построений; в этом случае перейти к пункту 8.
4. Найти на чертеже-наброске все элементы: точки, углы, отрезки и тому подобное, которые не даны непосредственно на чертеже-наброске, но легко определяются, используя данные в условии элементы и соотношения, связывающие эти данные (при этом полезно названия элементов сопровождать их различными определениями и выявлением их существенных свойств).
5. Найти такую часть искомой фигуры на чертеже-наброске (точка, угол, отрезок, дуга, треугольник), которая:
а) включает в себя «узловые точки» искомой фигуры;
б) может быть построена по известным элементам;
в) дает возможность построить искомую фигуру (ее «узловые точки»).
Целесообразнее всего в качестве такой части выбрать, если он присутствует на чертеже-наброске, треугольник, у которого хотя бы одна вершина совпадает с «узловыми точками» искомой фигуры.
6. Выяснить, какие «узловые точки» искомой фигуры остались еще неопределенными, и как они могут быть построены, выясняя их положение по свойствам, вытекающим из связей с известными элементами.
Для отыскания каждой точки можно использовать метод геометрических мест. Суть его такова: найти две линии, на пересечении которых и лежит данная точка.
7. Если положение остальных «узловых точек» не определяется, выяснить, используя критерий, достаточно ли для проведения анализа чертежа-наброска.
8. Необходимо ввести дополнительные линии, если данных на чертеже-наброске не достаточно:
а) не все элементы, данные в условии, изображены на чертеже-наброске явно;
б) нет построенных треугольников на чертеже-наброске.
9. Определить вид задания элементов в условии задачи и выбрать, используя критерии допустимости геометрических преобразований, необходимый метод (методы) геометрического преобразования фигур.
10. Дополнить чертеж-набросок, используя выбранный метод (методы) преобразования фигур, и проверить, полезна ли построенная дополнительная линия (линии) для решения, путем применения пунктов 4-6.
11. Выбрать вспомогательный треугольник из числа всех образовавшихся после преобразования чертежа-наброска строимых треугольников. В качестве вспомогательного треугольника необходимо выбрать такой треугольник, у которого:
а) наибольшее число вершин совпадает с «узловыми точками» искомой фигуры;
б) способ построения которого самый простой.
12. Вернуться к пункту 6.
Рассмотрим решение задачи.
Задача 1. Построить прямоугольный треугольник по его гипотенузе и сумме катетов.
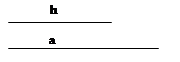
Дано: отрезки с и р (рис. 1а).
Построить: прямоугольный треугольник.
Анализ:
Пусть треугольник построен – АВС: АВ = с, <С = 90°, АС + ВС = р (рис. 1б).
Задача требует введения дополнительных линий, так как на чертеже-наброске явно не изображен отрезок р, равный сумме катетов искомого треугольника.
 A
A 
рис. 1а рис. 1б
В условии задачи все данные заданы по величине, причем отрезок р не изображен явно; части, составляющие его, образуют ломаную. Следовательно, можно применить метод спрямления, для этого дополним чертеж-набросок (описание данного метода и критериев применимости его автором описан в работе [1]).
Это можно сделать двумя способами:
1) отрезок ВС повернуть на 90° в положение СВ1 (рис. 1в).
Соединим точки В и В1, и получим треугольник АВВ1, который можно построить по двум сторонам: АВ = с, АВ1 = р и <АВ1В = 45°, противолежащему стороне АВ (основная задача). В данном треугольнике две вершины: А и В совпадают с «узловыми точками» искомой фигуры;
2) отрезок АС повернуть на 90° в положение СА1 (рис. 1г).
Соединим точки А и А1, и получим треугольник АВА1, который можно построить по двум сторонам: АВ = с, ВА1 = р и <АА1В = 45°. В данном случае две вершины А и В совпадают с «узловыми точками» искомой фигуры.
Так как в обоих случаях число вершин вспомогательного треугольника, совпавших с «узловыми точками», одинаковое (2), то для решения можно выбрать любой из этих треугольников, решения будут равноправными. Выберем, например, в качестве вспомогательного треугольник АВВ1.
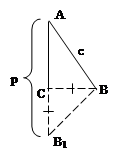

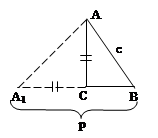
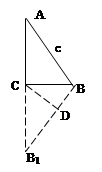
рис. 1в рис. 1г рис. 1д
Осталось выяснить, как можно построить третью «узловую точку» – С.
На чертеже-наброске (рис. 1в) треугольник ВВ1С равнобедренный по построению. Следовательно, если провести медиану СD к основанию ВВ1, то она по свойству равнобедренного треугольника будет также являться и высотой (рис. 1д).
Таким образом, понятно построение точки С:
1) строим серединный перпендикуляр к стороне ВВ1;
2) найдем точку пересечения построенного перпендикуляра с прямой АВ1 – точка С.
Все «узловые точки» искомой фигуры, таким образом, определены. Отсюда понятно построение искомого прямоугольного треугольника.
В заключение отметим, что предложенная методика проведения анализа в задачах на построение с помощью системы наводящих вопросов и правила-ориентира способствует лучшему усвоению процесса поиска решения задач в целом и на построение в частности.
Рецензенты:Гусев В.А., д.п.н., профессор, заведующий кафедрой теории и методики обучения математике Московского педагогического государственного университета, г. Москва.
Михайлов П.Н., д.ф.-м.н., профессор, ученый секретарь ГАНУ «Институт прикладных исследований республики Башкортостан», г. Стерлитамак.



