Введение

Работа посвящена исследованию смешанной задачи для гиперболического уравнения с оператором Бесселя с нелокальным интегральным условием второго рода.

Смешанные задачи для гиперболических уравнений с интегральными нелокальными условиями рассматривались в работах Д.Г. Гордезиани и Г.А. Авалишвили [3], Л.С. Пулькиной [6; 7], А. Бузиани [9] и других авторов. Классические методы не всегда применимы к исследованию нелокальных задач с интегральными условиями, поэтому вопрос разработки методов исследования таких задач остается актуальным и в настоящее время.

Результаты настоящей работы являются продолжением исследований смешанных задач с нелокальными интегральными условиями для гиперболических уравнений [4; 5; 7].

Постановка смешанной задачи с интегральным условием второго рода

Пусть – прямоугольная область в координатной плоскости Oxt, .

В области D рассмотрим В-гиперболическое уравнение вида

, (1)

где – оператор Бесселя, – заданное действительное число.

Требуется найти функцию , удовлетворяющую условиям:

, (2)

, , (3)

, , (4)

, , , (5)

, , (6)

где и – заданные, достаточно гладкие функции.

Единственность решения смешанной задачи (2)-(6)

Теорема 1. Смешанная задача (2)-(6) с интегральным условием (6) не может иметь более одного решения.

Доказательство. Докажем теорему методом от противного. Пусть и - два предполагаемых решения задачи (2)-(6). Тогда их разность удовлетворяет условиям (2)-(4) задачи (2)-(6), однородным начальным условиям

, ()

и однородному интегральному условию

. ()

Нетрудно проверить, что имеет место тождество

.

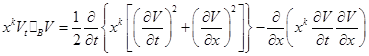Полагая в этом тождестве , с учетом того, что является решением уравнения (1), получим

.

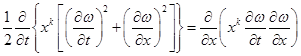Интегрируя последнее тождество по x на отрезке , имеем

, (7)

где

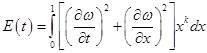. (8)

Умножая уравнение (1) на и интегрируя его по x на отрезке , получим:

. (9)

Заменим в условии () на его значение из (9), в результате чего будем иметь

. (10)

Полагая здесь , получим уравнение , общее решение которого имеет вид , а значит .

В силу начальных условий (): и , и, следовательно, , поэтому согласно () , а, значит, из (8) и (9) получаем

.

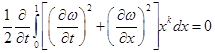Таким образом:

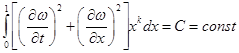. (11)

Полагая в (11) , с учетом начальных условий (), получаем , а значит

,

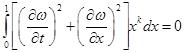откуда следует: и , т.е., . Из этого равенства и начальных условий () следует, что . Таким образом, получили, что и . Теорема доказана.

Построение частных решений уравнения (1) в прямоугольной области

Сначала построим систему частных решений уравнения (1), удовлетворяющих условиям

, (12)

, , (13)

, , (14)

, . (15)

Частное решение уравнения (1) ищем в виде

, (16)

где X и T – пока неопределенные функции. Их найдем из требования, чтобы функция (16) удовлетворяла условиям (12)-(15). С этой целью подставим ее в уравнение (1) и граничные условия (14) и (15).

, (17)

, (18)

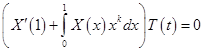. (19)

Разделяя переменные в уравнении (17) и сокращая на T равенства (18) и (19), получим обыкновенные дифференциальные уравнения и условия относительно неопределенных функций

, (20)

, (21)

, (22)

. (23)

Найдем общее решение уравнения (21), т.е. уравнения . Умножим это уравнение на и произведем замену переменных по формулам 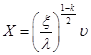, . В результате уравнение приводится к уравнению Бесселя

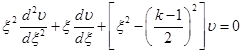. (24)

Пусть – нецелое число. Тогда общее решение этого уравнения имеет вид [2]

, (25)

где – функции Бесселя первого рода.

Возвращаясь к старым переменным в (25), имеем

, (26)

где – произвольные постоянные. Их найдем из требования, чтобы общее решение (26) удовлетворяло условиям (22) и (23). С этой целью подставим его в эти условия.

В силу известной формулы дифференцирования функции Бесселя [8]

.

Также в силу известной при асимптотической формулы функции Бесселя [1] при : , а при : .

Полагая в общем решении (26) , получим . Здесь также положим , так как собственные функции определяются с точностью до постоянного множителя. Таким образом, решение уравнения (21), удовлетворяющее условию (22), имеет вид

. (27)

Подставим (27) в условие (23): , откуда .

В результате подстановки имеем

. (28)

Известно [2], что

. (29)

Вычисляя интеграл в (28) с помощью формул (29) и Ньютона-Лейбница, получим: . Отсюда и из (28) имеем: или

. (30)

Пусть – положительные корни уравнения (30), расположенные в порядке возрастания. Тогда числа определяют собственные значения спектральной задачи. Полагая в (27) , получим соответствующие собственные функции

(31)

Докажем, что система функций (31) ортогональна в промежутке [0,1] с весом . Функция (27) является решением уравнения (21), т.е.

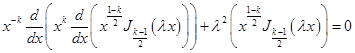. (32)

Умножая равенство (32) на , получим

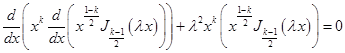
или

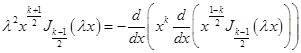. (33)

Полагая в этом равенстве и , имеем

,

.

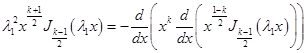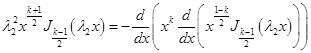Умножим первое из этих равенств на , а второе на , после чего вычтем первое равенство из второго. В результате получим после несложных преобразований

(34)

.

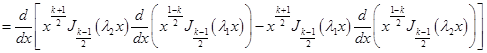Вычисляя в равенстве (34) внутренние производные, получим

.

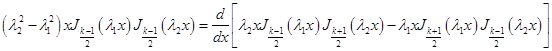Интегрируя это равенство по x на отрезке [0,1], получаем

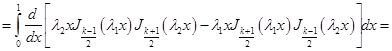
. (35)

Таким образом, доказано, что система функций 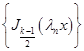ортогональна с весом x в промежутке [0,1]. Отсюда следует, что система функций (31) ортогональна с весом в промежутке [0,1].

Полагая в уравнении (20) , получим Общее решение этого уравнения имеет вид

Таким образом, система частных решений уравнения (1), удовлетворяющих условиям (12)-(15), определяется по формуле

(36)

а окончательное решение поставленной задачи имеет вид

(37)

где коэффициенты разложения определяются по формулам

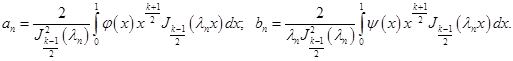
Рецензенты:

Игнатьев Ю.Г., д.ф.-м.н., профессор, заведующий кафедрой высшей математики и математического моделирования Института математики и механики им. Н.И. Лобачевского, Казанский (Приволжский) федеральный университет, г. Казань.

Сушков С.В., д.ф..-м.н., профессор, заведующий кафедрой теории относительности и гравитации Института физики, Казанский (Приволжский) федеральный университет, г.Казань.