Метаметодика, как современное научное педагогическое направление, строится на основе интеграции предметных методик с целью выделения специфики каждой. Ее построение предполагает выход конкретных методик на философский уровень через установление связей между методиками конкретных дисциплин как в содержательном (через установление связи значений понятий, обозначенных одним и тем же термином в разных предметах), так и деятельностном аспектах. Целостность образовательного процесса, интеграция учебных предметов обеспечивается метаметодическим подходом. Метаметодика понимается как интеграция предметных методик с сохранением специфики каждой и учетом субъектного опыта учащихся [4]. Формирование метапредметных умений и навыков исследовательской деятельности является приоритетным направлением совершенствования физико-математического образования на современном этапе.
Одним из кардинальных изменений физического образования становится его методологическая направленность. Необходимость изучения научной методологии вызвана не только научно-техническим прогрессом, но и коренным изменением характера научных знаний, самого процесса познания и взаимоотношения знания и познания. Резко повысился методологический уровень знаний, усложнился процесс научного познания, изменилось соотношение между исследованием и изложением научных знаний: они частично проникают друг в друга. Сегодня необходимо добиваться, чтобы для учащихся наука была не перечнем открытий, не суммой формул, а способом мышления в процессе познания окружающего мира, логическим подходом к решению проблем [3].
Цель исследования. Обсуждение и поиск путей решения проблемы отбора содержания физических задач в рамках метаметодической модели обучения в вопросах истории и методологии науки. Развитие задачного подхода в метаметодике на основе концепции «образование как учебная модель науки», а также исследование дидактических функций задач в плане формирования межпредметных понятий и метапредметных умений с использованием современных методов математического и компьютерного моделирования в учебно-иссле-довательской деятельности.
Методы исследования. В работе применялись общетеоретические и экспериментальные методы педагогических исследований. Проектирование методической системы обучения физике носит общетеоретический (прогностический) характер. В связи с этим решалась проблема экспериментальной проверки полученного результата (метаметодической модели обучения физике) в ходе опытно-экспериментальной работы авторов в школе и вузе, апробации результатов педагогических исследований на международных и всероссийских научно-практических конференциях, проводимых в РГПУ им. А.И. Герцена и СПбГУКиТ.
Результаты исследования и их обсуждение
В теории и методике обучения физике решение задач рассматривается преимущественно как метод обучения и как средство закрепления теоретического материала, развития мышления и творческих способностей обучаемых в условиях реализации межпредметных связей математических и естественно-научных дисциплин. Дидактические функции задач не потеряли своего значения и в метаметодике учебных исследований.
Математика продолжает активно развиваться и, будучи самой фундаментальной из наук, все равно (а может, именно поэтому) имеет много практических применений. Интересно, что, несмотря на бурное развитие в последние двести лет, задачи математики не стали более заумными. Ну... скажем так, - не все стали более заумными. Конечно, многое меняется, новые понятия вводятся на базе старых, все стало сложнее, чем в XIX веке. Но при этом по-прежнему есть задачи, которые можно объяснить на пальцах школьнику, если уж не решения, то формулировку [6].
История теории протекания началась с нескольких задач, которые поставили перед математиками физики-экспериментаторы, а именно - с того, что они действительно наблюдали в природе. В данном случае можно говорить о межпредметных понятиях: теория, эксперимент и модель, а также о понятиях, сводимых к межпредметным: перколяция, кластер и фрактал.
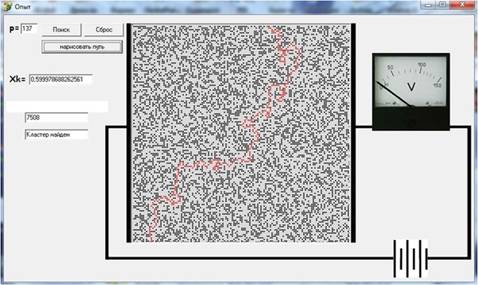
Рис. 1. Компьютерная модель задачи о перколяции.
Американские физики в 1974 г. провели опыт, в котором они использовали обычную экранную сетку. Сетка имела квадратную форму и содержала 137x137 узлов с расстоянием 6,35 мм между соседними узлами. К двум противоположным концам сетки были припаяны два электрода. В опыте определялся критический параметр разрыва цепи (появления соединяющего кластера на квадратной решетке). Компьютерная модель в цикле занимательных физических задач обсуждается в статье [2] (рис. 1).
Похожие формы наблюдали в реальных ситуациях. Вот, скажем, лесные пожары: когда у вас выгорает кусок леса, то граница его становится фракталом, причем экспериментально установлено, что обычно это фракталы размерности 4/3. То же самое с фронтами эрозии или просачиванием жидкости через пористую среду [6].
Теорема о размерности фрактала в задачах перколяции доказана Венделеном Вернером, лауреатом премии Филдса 2006 года. При решении физической задачи оказалось, что первыми ее поставили математики, просто про это успели забыть. Более того, ее поставили в журнале для школьников и учителей математики, американском родственнике «Кванта» - в журнале «American Mathematical Monthly», в первый год ее издания - 1894, более века назад. Этот журнал и сейчас популярен, его издает Математическая ассоциация Америки - объединение учителей и просто любителей математики. Там есть примерно такая же серия, как «Задачник «Кванта», только иногда предлагаются задачи, где решение неизвестно. Порой они оказываются очень сложными и ведут к интересным математическим теориям - так, например, случилось и с задачей о росте групп, поставленной Джоном Милнором в 1968 году и решенной Р.И. Григорчуком в 1984 году [6].
Другая интересная черта перколяции в том, что она связана со многими другими явлениями, даже из классической науки, которую проходят в школе. Есть случайный процесс, который упоминается в курсах биологии и физики, - броуновское движение. Роберт Браун, шотландский ботаник, открывший ядро клетки, в 1827 году увидел в микроскоп хаотическое движение маленьких частичек внутри зернышек пыльцы. И он тогда очень серьезно к этому подошел. До него многие наблюдали это движение, например швед Ян Ингенхауз, но Браун серьезно подошел к исследованиям и правильно поставил вопрос.
Дискретную модель диффузии можно моделировать на решетке. И в пределе, если смотреть издалека и если брать очень маленькие молекулы, это будет непрерывный процесс, который называют броуновским движением или процессом Винера. И опять же, вне зависимости от того, какую мы жидкость возьмем и на какой решетке смоделируем, траектории будут одни и те же. И что самое интересное - есть универсальность даже на уровне связи с перколяцией: у траекторий броуновского движения граница тоже будет размерности 4/3, и это будет та же самая кривая, что для кластера перколяции [6].
Модельный характер всех наших знаний приводит к сближению физических и математических моделей. Характерной чертой научной деятельности является исключительная трудность, а порой и невозможность отделения физической и математической модели при рассмотрении достаточно сложных реальных явлений.
Вспомним точку зрения выдающегося математика В.И. Арнольда: «Математика, подобно физике, - экспериментальная наука, отличающаяся от физики лишь тем, что в математике эксперименты очень дешевы … Математика является экспериментальной наукой – частью теоретической физики и членом семейства естественных наук. Основные принципы построения и преподавания всех этих наук применимы и к математике… Умение составлять адекватные математические модели реальных ситуаций должно составлять неотъемлемую часть математического образования… При всем огромном социальном значении вычислений (и computer science), сила математики не в них, и преподавание математики не должно сводиться к вычислительным рецептам» [1].
В начале ХХ века внимание многих ученых было привлечено к различным задачам физики твердого тела. Их интересовало, можно ли предсказывать теплоемкость твердых тел на основе простых представлений о движении и взаимодействии отдельных частиц, как в кинетической теории газов. Проблема хаотизации колебаний атомов в нелинейном кристалле (термализация) восходит к работам П. Дебая (1914).
Позднее, в 50-х годах, Э. Ферми были инициированы вычислительные эксперименты в физике твердого тела на одной из первых ЭВМ. Дж. Паста и С. Улам рассчитывали динамику 64 связанных осцилляторов с нелинейными силами взаимодействия. Вместо термализации энергии обнаруживались солитонные решения в нелинейной среде. Кроме того, наблюдался парадокс возврата системы к начальному состоянию. Совокупность изучаемых вопросов численного моделирования стали называть проблемой Ферми – Паста - Улама (ФПУ) [7].
Актуальность изучения вопросов физики нелинейных явлений связана с тем, что идеи, методы и результаты физики открытых систем, в частности нелинейной динамики, служат фундаментом педагогической и научной деятельности специалистов разного профиля - физиков и математиков, химиков и биологов, экономистов и социологов.
Одним из центральных в современной физике является представление о нелинейных явлениях, в частности о механизмах рассеяния носителей заряда в физике конденсированного состояния. В этой связи необходимо понимание того, что в идеально-периодической структуре (идеальный кристалл) электронная волна распространяется без рассеяния, и последнее возникает на структурных неоднородностях [7].
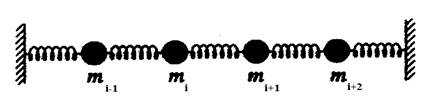
Рис. 2. Историческая задача вычислительной физики.
Для формирования понятий и представлений в физике конденсированного состояния, изучения численных методов математического и компьютерного моделирования может быть полезна известная механическая модель-цепочка Ферми – Паста - Улама с системой дифференциальных ньютоновских уравнений: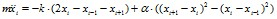 
, 
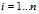и однородными граничными условиями 
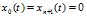(рис. 2).
Очевидно, размерность многомерного фазового пространства (пространства координат и импульсов) исторических задач вычислительной физики ограничивалась техническими возможностями первых ЭВМ. Сегодня использование современного программного и математического обеспечения в учебном компьютерном эксперименте позволяет «качать» сотни связанных осцилляторов, наблюдая нелинейные волновые процессы и спектры колебаний средствами интерактивной компьютерной графики (с помощью ИКГ-систем) (рис. 3). Оптимальная техника программирования с использованием численных методов, функций символьных преобразований в системах компьютерной математики (например, в программе Maple) обеспечивает минимальный размер файла программы вычислительного эксперимента, текст которой может состоять из нескольких строк, написанных на удобном алгоритмическом языке.
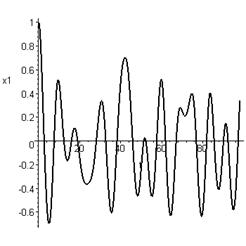
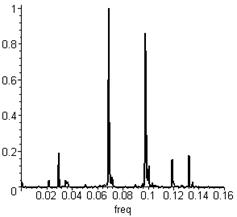
Рис. 3. Спектральный анализ колебаний в цепочке связанных осцилляторов.
Изучая межпредметные связи физики и математики в контексте метаметодики учебных исследований, уместно вспомнить А. Пуанкаре: «все законы выводятся из опыта. Но для их выражения нужен специальный язык. Обиходный язык слишком беден, кроме того, он слишком неопределенен для выражения столь богатых содержанием точных и тонких соотношений. Таково первое основание, по которому физик не может обойтись без математики; она дает ему единственный язык, на котором он в состоянии изъясняться». Чтобы вывести закон из опыта, необходимо обобщать. Какими критериями следует руководствоваться при проведении этих обобщений? Как отмечает А. Пуанкаре, «руководителем может быть только аналогия… Но кто же научил нас познанию истинных, глубоких аналогий, таких, которые не видит глаз, но которые отгадывает разум? Этому научил нас математический ум, который пренебрегает содержанием, чтобы иметь дело только с чистой формой. Это он научил нас называть одним и тем же именем все сущности, отличающиеся только своим содержанием»
[5].
Заключение
В системе современных знаний физика продолжает формировать стиль научного мышления, задает его нормы, т.е. остается лидером современного естествознания. Овладение основами физического мышления должно осуществляться в определенных формах и методах обучения. Речь идет о вооружении учащихся знанием истории и методологии науки, сознательного использования метапредметных умений и навыков исследовательской деятельности.
Педагогические исследования показывают, что материал, вызывающий положительные эмоции, усваивается легче, чем безразличный и скучный. Как считал А.Эйнштейн, «где только возможно, изучение должно стать переживанием, и этот принцип будет проведен в жизнь будущей реформой школы». Исторические задачи с компьютерным экспериментом, физические парадоксы как раз и являются тем эффективным средством изучения учебного материала, который вызывает определенные эмоциональные, этические и эстетические переживания [3].
Заметим, что для развития навыков научно-исследовательской деятельности при изучении истории физических задач можно эффективно использовать и современные, актуальные проблемы с метапредметными понятиями. Полученные решения могут содержать существенные научные результаты [3; 7; 8]. К тому же выбираемая проблема должна лежать на стыке двух или даже нескольких областей знания. Это связано с дидактическим требованием доступности: научные проблемы в рамках развитых областей знаний - физики или математики, как правило, сложны и недоступны для решения на образовательном уровне.
Рецензенты:
Горбунова И.Б., д.п.н., профессор кафедры информатизации образования, главный научный сотрудник учебно-методической лаборатории «Музыкально-компьютерные технологии» ФГБОУ «Российский государственный педагогический университет им. А.И. Герцена», г.Санкт-Петербург.
Смирнов Н.В., д.ф.-м.н., доцент, профессор кафедры моделирования экономических систем факультета прикладной математики процессов управления Санкт-Петербургского государственного университета, г. Санкт-Петербург.