В целом ряде прикладных задач используется дисперсия реакции линейного динамического объекта (ЛДО) на включение стационарного случайного воздействия (ССВ) с известной дисперсией 
и нормированной корреляционной функцией (НКФ) 
. Искомая дисперсия определяется известным способом [1–3]:
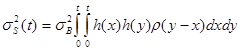, (1)
где 
– импульсная характеристика (ИХ) ЛДО.
Для произвольного ЛДО и произвольной экспоненциально-косинусной НКФ дисперсия (1) приобретает форму табличных интегралов. Однако получаемые выражения для ЛДО второго порядка и выше, а также НКФ, имеющие вид сложнее простой экспоненты, имеют настолько сложный конечный вид, что не позволяют в общем виде исследовать свойства дисперсии и, в частности, быстро оценить её предельные значения.
Цель исследования – получение упрощенных оценок дисперсий реакции ЛДО на включение ССВ.
Метод исследования
В основе метода исследования лежит способ представления (1) для экспоненциально-косинусных НКФ с аргументом под знаком модуля [2]:
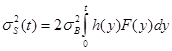, (2)
где
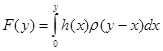. (3)
Функционал 
есть свертка функций 
и 
и совпадает по форме с реакцией ЛДО на детерминированный сигнал вида . Такое совпадение позволяет сравнительно просто оценить (3) сверху и затем использовать полученную оценку для оценки дисперсии (2).
В работах [3, 4] описан метод получения оценки предельных значений реакции ЛДО, на ограниченное по динамическому диапазону детерминированное воздействие. Форма записи анализируемой реакции несколько отличается от , но данный метод полностью применим и к (3), который также следует рассматривать как площадь, ограниченную произведением функций и 
. Второй сомножитель в следует считать функцией , взятой с обратным знаком аргумента 
, и смещенной в точку 
, для которой определяется значение (3). Предлагаемое представление упрощает нахождение такого вида НКФ, который максимизирует (3) для данной ИХ. В зависимости от поведения ИХ процедуру определения оценки дисперсии целесообразно рассмотреть отдельно для знакопеременных и знакопостоянных ИХ.
Результаты исследования и их обсуждение
Рассмотрим реакцию ЛДО со знакопостоянной ИХ на воздействие ССВ со знакопостоянной НКФ. В этом случае функционал (3) приобретает максимально возможное значение при 
, что значительно упрощает нахождение оценки предельно возможного значения дисперсии (2). Теперь, зная максимизирующий вид НКФ ССВ, дисперсию реакции определим непосредственно по (2) и окончательно получим:
, (4)
где 
– переходная характеристика ЛДО,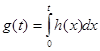 
.
Для ЛДО со знакопеременной ИХ реакцию следует оценивать по интервалам знакопостоянства ИХ. Любая пара нулей 
знакопеременной ИХ задает границы интервалов её знакопостоянства. Первый интервал знакопостоянства ограничен слева 
, независимо от значения 
.
На основе подхода, изложенного в [3, 4], можно утверждать, что для знакопеременной ИХ предельное значение (3) достигается в случае, если 
принимает значение 
или 
в пределах текущих интервалов знакопостоянства ИХ. При этом в точке 
всегда 
. На рисунке 1 пунктиром показаны максимизирующие НКФ для значений 
, соответствующих различным интервалам знакопостоянства ИХ.
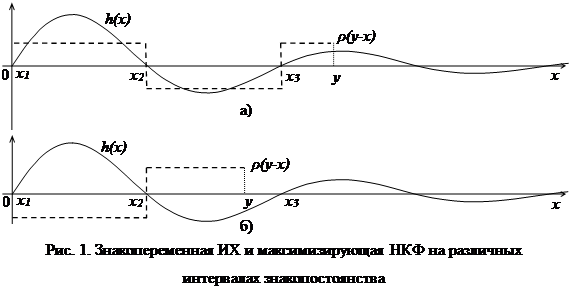
Тогда на произвольном 
-м интервале знакопостоянства ИХ функционал (3) примет значение:
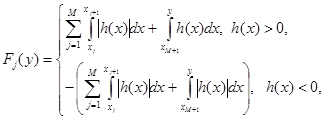(5)
где 
– число полных интервалов знакопостоянства ИХ на интервале от 0 до .
В конце текущего интервала знакопостоянства ИХ, т.е. при 
, функционал (3) от максимизирующей НКФ достигнет максимально возможного значения по модулю:
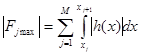. (6)
Таким образом (6) есть оценка сверху функционала (3) по модулю на произвольном -м интервале знакопостоянства ИХ, при этом знак 
совпадает со знаком :
, 
.
Теперь дисперсию (2) определяем по интервалам знакопостоянства ИХ, где вместо используем соответствующие интервалам оценки 
. Тогда (2) преобразуется к виду:
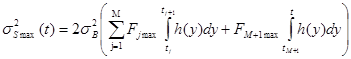, (7)
где – число полных интервалов знакопостоянства ИХ на интервале от 0 до 
;
– нули ИХ, границы интервалов знакопостоянства ИХ.
Для ЛДО со знакопеременной ИХ оценка (7) подлежит уточнению следующим образом. На первом интервале знакопостоянства 
функционал (3) принимает максимальное значение при и максимальное текущее значение дисперсии совпадет с (4). В конце интервала
, (8)
где 
– второй (или первый для ИХ с 
) нуль ИХ и одновременно верхняя граница первого интервала знакопостоянства ИХ. В то же время согласно (7) на первом интервале знакопостоянства текущее значение оценки дисперсии примет вид 
, а в конце интервала
. (9)
Двукратное завышение оценки дисперсии (9) объясняется тем, что на интервалах знакопостоянства функционал (3) оценивается предельно возможным значением, принятым за постоянное на всем интервале.
Если потребовать, чтобы в точке оценка не превышала (8) тогда (7) преобразуется к виду
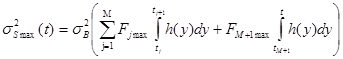. (10)
Поскольку знаки оценки (6) функционала (3) и всегда совпадают, то (10) имеет вид монотонно нарастающей функции без локальных максимумов и минимумов. Определение оценки (10) не требует громоздких выкладок, позволяет достаточно просто и инвариантно к НКФ оценить сверху дисперсию реакции для любого ЛДО.
На рисунке 2 представлен пример оценки (а) дисперсии (б) реакции ЛДО со знакопеременной ИХ 
(
) на включение ССВ с НКФ вида 
, 
, 
.
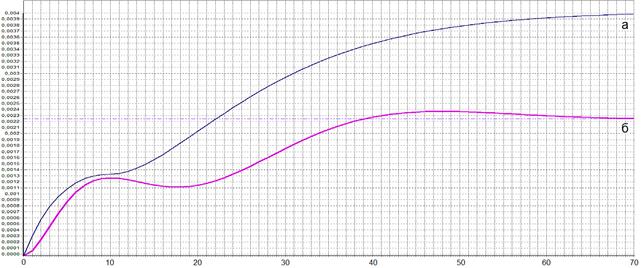
Рис. 2
Общий вид дисперсии реакции:
, (11)
где 
– коэффициенты, зависящие от параметров 
, 
, 
.
ИХ имеет два интервала знакопостоянства, разделенных нулем 
. Функционал (3) на первом и втором интервалах знакопостоянства примет значение 
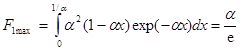и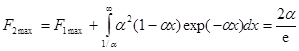 
соответственно. Тогда оценка дисперсии по двум интервалам знакопостоянства примет вид:
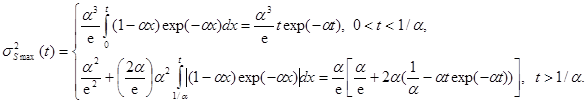(12)
Оценка (12) представляет собой монотонно нарастающую функцию без локальных максимумов и минимумов, ограниченную значением 
. Оценка (12) значительно проще дисперсии (11).
Заключение
Для ЛДО со знакопостоянной ИХ искомая оценка с точностью до постоянного множителя равна квадрату переходной характеристики. Для ЛДО со знакопеременной ИХ искомая оценка содержит взвешенные суммы интегралов от ИХ на интервалах знакопостоянства. Весовые коэффициенты представляют собой сумму интегралов от модулей ИХ по интервалам знакопостоянства. Полученные оценки имеют значительно более простой вид, чем исходное выражение и дают возможность быстро оценить предельные границы диапазона дисперсии выходной реакции ЛДО для ССВ с произвольной НКФ.
Рецензенты:
Ширапов Д.Ш., д.ф.-м.н., профессор, заведующий кафедрой «Электронно-вычислительные системы» ФГБОУ ВПО «Восточно-Сибирский государственный университет технологий и управления», г. Улан-Удэ.
Мижидон А.Д., д.т.н., профессор, заведующий кафедрой «Прикладная математика», ФГБОУ ВПО «Восточно-Сибирский государственный университет технологий и управления», г. Улан-Удэ.
Лубенцов В.Ф., д.т.н., профессор, зам. директора по научной работе, профессор кафедры «Информационные системы, Электропривод и автоматика», Невинномысский технологический институт ГОУ ВПО «Северо-Кавказский государственный технический университет», г. Невинномысск.