К производительности электронных вычислительных машин, работающих в режимах реального времени, предъявляются высокие требования. Этими требованиями обусловливаются усилия электронщиков и математиков, направленные на разработку новых высокопроизводительных вычислительных систем. Вот некоторые направления приложения сил: создание новых вычислительных архитектур (применяются распараллеливание и конвейеризация вычислительных процессов), поиск и отбор среди известных численных методов тех, которые допускают распараллеливание и конвейеризацию, построение плотных расписаний и т.д.
В частности, для выполнения первого этапа решения систем линейных уравнений, разработана систолическая система (матрица) Джентльмена-Кунга, приводящая матрицу исходной системы к треугольному виду [1]. Для решения системы уравнений с верхней треугольной матрицей (второй этап) используется систолическая структура, реализующая обратный ход метода Гаусса [1]. Вычислительными элементами матрицы Джентльмена-Кунга являются, устройства Cordic, которые осуществляют преобразования вращения. Это обеспечивает вычислительному процессу наибольшую вычислительную устойчивость (преобразования вращения нечувствительны к ошибкам округления), чего нельзя сказать об обратном ходе метода Гаусса. Вычисления здесь ведутся по формуле
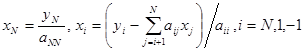 .
.
Выражение ![]() следует читать так: i изменяется от
следует читать так: i изменяется от ![]() до 1 с шагом –1. Моделирование и анализ погрешностей обратного хода метода Гаусса для систем с двухдиагональной матрицей можно найти [4, стр. 27]. Вычисление суммы
до 1 с шагом –1. Моделирование и анализ погрешностей обратного хода метода Гаусса для систем с двухдиагональной матрицей можно найти [4, стр. 27]. Вычисление суммы ![]() представляет собой вычисление скалярного произведения i-ой строчки матрицы А на вектор х. Оценку точности вычисления скалярного произведения векторов с обычной точностью, можно найти в [5, стр. 249, (5.16)]
представляет собой вычисление скалярного произведения i-ой строчки матрицы А на вектор х. Оценку точности вычисления скалярного произведения векторов с обычной точностью, можно найти в [5, стр. 249, (5.16)]
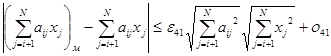 , где
, где![]() (Частичные суммы скалярного произведения продвигаются по систолической структуре, реализующей обратный ход метода Гаусса, от одного вычислительного элемента к другому с обычной точностью).
(Частичные суммы скалярного произведения продвигаются по систолической структуре, реализующей обратный ход метода Гаусса, от одного вычислительного элемента к другому с обычной точностью).
Погрешности, характеризуемые произведением 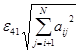 , относят к эквивалентному возмущению матрицы системы А. Из последних соотношений видно (см. на число (i – 1)), что вычисления обратного хода метода Гаусса обусловлены хуже, чем исходная задача. Следует отметить, что если скалярное произведение вычислять с расширенной точностью, то обратный ход метода Гаусса приобретает устойчивость, в этом случае
, относят к эквивалентному возмущению матрицы системы А. Из последних соотношений видно (см. на число (i – 1)), что вычисления обратного хода метода Гаусса обусловлены хуже, чем исходная задача. Следует отметить, что если скалярное произведение вычислять с расширенной точностью, то обратный ход метода Гаусса приобретает устойчивость, в этом случае ![]() , [5, стр. 249, (5.16)].
, [5, стр. 249, (5.16)].
Со своей стороны математики-вычислители стараются разработать новые аппаратурно-ориентированные алгоритмы, отвечающие указанным выше требованиям.
Ниже предлагается метод решения систем линейных уравнений с верхней треугольной матрицей, в котором используются так называемые локальные матрицы вращения (изменяющие только смежные компоненты вектора):
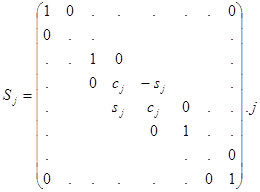
а также локальные матрицы перестановки строк

Последние описывают продвижение обрабатываемых данных по вычислительной структуре (систолической матрице).
Описание метода ортогонального обратного хода
Пусть матрица А системы уравнений ![]() имеет треугольный вид. Составим расширенную систему
имеет треугольный вид. Составим расширенную систему ![]() , введем обозначение
, введем обозначение ![]() и перейдем к изложению алгоритма.
и перейдем к изложению алгоритма.
Предварительный (нулевой) шаг. Вычислим ![]() по формуле
по формуле ![]() .
.
Шаг 1. Подберем пару чисел ![]() такую, чтобы (N – 1)-я компонента N-ого столбца матрицы
такую, чтобы (N – 1)-я компонента N-ого столбца матрицы ![]() обратилась ноль. Здесь
обратилась ноль. Здесь ![]() – локальное преобразование вращения, определенное парой
– локальное преобразование вращения, определенное парой ![]() . При этом матрица
. При этом матрица ![]() примет вид
примет вид
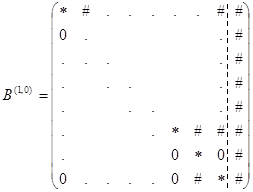
Употребляемые здесь знаки имеют следующие значения: 0 – обязательно нулевой элемент, ![]() – обязательно ненулевой элемент, # – элемент, значение которого мы не оговариваем. Произведем перестановку N-ой и (N – 1)-ой строк матрицы
– обязательно ненулевой элемент, # – элемент, значение которого мы не оговариваем. Произведем перестановку N-ой и (N – 1)-ой строк матрицы ![]() :
: ![]() , в результате получим
, в результате получим
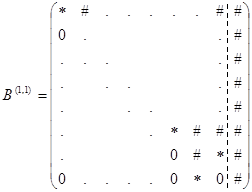 .
.
Вычислим ![]() по формуле
по формуле ![]() .
.
Шаг 2. Подберем пару чисел ![]() такую, чтобы (N – 2)-я компонента N-ого столбца матрицы
такую, чтобы (N – 2)-я компонента N-ого столбца матрицы ![]() приняла нулевое значение, при этом матрица
приняла нулевое значение, при этом матрица ![]() примет вид.
примет вид.
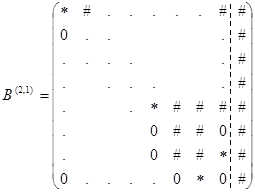
Произведем перестановку (N – 1)-ой и (N – 2)-ой строк матрицы ![]() :
: ![]() , в результате получим
, в результате получим
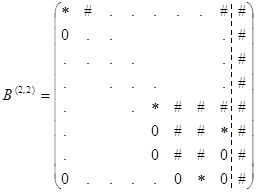 .
.
Шаг 3. Определим пары чисел ![]()
![]() так, чтобы (N – 1)-я компонента (N – 1)-ого столбца и (N – 3)-я компонента N-ого столбца матрицы
так, чтобы (N – 1)-я компонента (N – 1)-ого столбца и (N – 3)-я компонента N-ого столбца матрицы ![]() приняли нулевое значение, при этом матрица
приняли нулевое значение, при этом матрица ![]() примет вид
примет вид
 .
.
Поменяем местами строки N-ю с (N – 1)-ой и (N – 2)-ю с (N – 3)-ой: ![]() , в результате получим
, в результате получим
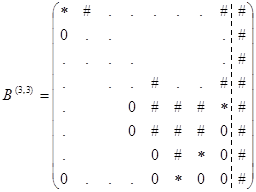
Затем вычислим ![]() .
.
Шаг 4. Определим пары чисел ![]()
![]() так, чтобы (N – 2)-я компонента (N – 1)-ого столбца и (N – 4)-я компонента N-ого столбца матрицы
так, чтобы (N – 2)-я компонента (N – 1)-ого столбца и (N – 4)-я компонента N-ого столбца матрицы ![]() приняли нулевое значение, при этом матрица
приняли нулевое значение, при этом матрица ![]() примет вид
примет вид
 .
.
Поменяем местами строки: (N – 1)-ю с (N – 2)-ой и (N – 3)-я с (N – 4)-я: ![]() , в результате получим матрицу
, в результате получим матрицу
 .
.
Шаг i (i = 5, N – 1). Подберем пары чисел ![]() где
где ![]()
![]()
![]() , такие, чтобы элементы
, такие, чтобы элементы ![]() матрицы
матрицы ![]() приняли нулевое значение (здесь
приняли нулевое значение (здесь ![]() – целая часть частного от деления (i + 1) на 2), при этом матрица
– целая часть частного от деления (i + 1) на 2), при этом матрица ![]() , если i нечетно, примет вид
, если i нечетно, примет вид
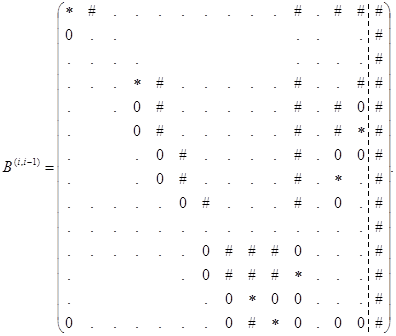
Осуществим перестановку строк: ![]() , в результате получим матрицу
, в результате получим матрицу

Отсюда видно, что ![]() .
.
Если i четно, то матрица ![]() примет вид
примет вид
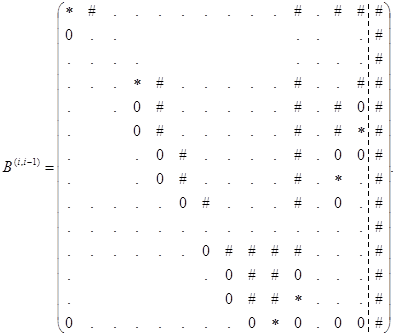
Осуществим перестановку строк: ![]() , в результате получим матрицу
, в результате получим матрицу
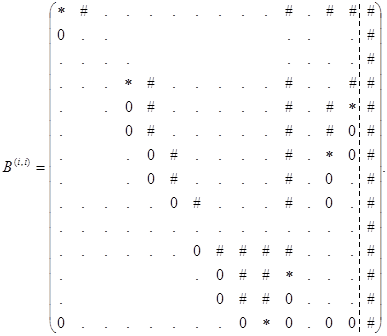
Шаг i (i = N, 2(N – 1) – 1). Подберем пары чисел ![]() где
где ![]()
![]() ,
,![]() ,
,![]() , такие, чтобы элементы
, такие, чтобы элементы ![]() матрицы
матрицы ![]() приняли нулевое значение (здесь
приняли нулевое значение (здесь ![]() – целая часть частного от деления (i+1) на 2), при этом матрица
– целая часть частного от деления (i+1) на 2), при этом матрица ![]() , если i нечетно, примет вид
, если i нечетно, примет вид

Осуществим перестановку строк: ![]() в результате получим матрицу
в результате получим матрицу
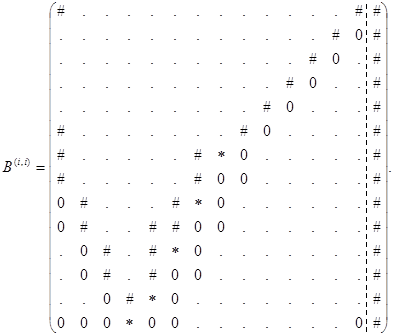
Отсюда видно, что ![]() .
.
Если i четно, то матрица ![]() примет вид
примет вид

Осуществим перестановку строк: ![]() , в результате получим матрицу
, в результате получим матрицу
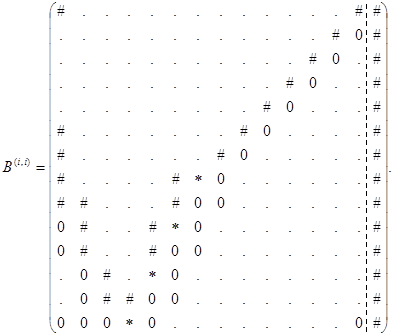
Замечание 1. Применение формулы ![]() основано на том факте, что при нечетном i в N-ой строке все элементы расширенной матрицы
основано на том факте, что при нечетном i в N-ой строке все элементы расширенной матрицы ![]() за исключением
за исключением ![]() и, возможно,
и, возможно, ![]() равны нулю (матрица А невырождена).
равны нулю (матрица А невырождена).
Замечание 2. Более наглядный и простой вывод формул без указания перестановок строк дан в [2].
Перейдем к упрощенному описанию систолической структуры, реализующей предложенный метод, и вычислительных элементов (ВЭ), входящих в ее состав. Эта структура состоит из ВЭ трех типов.
Первый ВЭ. Он имеет один вход, два выхода и внутренний регистр (ВР) для хранения вычисленного результата (обозначение ![]() ). Будем предполагать, что на регистре имеется вычисленный результат – у, а на его вход поступает число х (х,у – компоненты двумерного вектора
). Будем предполагать, что на регистре имеется вычисленный результат – у, а на его вход поступает число х (х,у – компоненты двумерного вектора ![]() , тогда функционирование ВЭ можно описать следующим образом: на первый и второй выходы поступают c и s, на ВР – у, где с,s и у определяются соотношениями
, тогда функционирование ВЭ можно описать следующим образом: на первый и второй выходы поступают c и s, на ВР – у, где с,s и у определяются соотношениями ![]() ,
, ![]() ,
, ![]() .
.
Второй ВЭ. Он имеет три входа, один выход и внутренний регистр (ВР) для хранения вычисленного результата (обозначение ![]() ). Будем предполагать, что на регистре имеется вычисленный результат – v, а на его первый вход поступает число u, на второй и третий – с и s (u,v – компоненты двумерного вектора
). Будем предполагать, что на регистре имеется вычисленный результат – v, а на его первый вход поступает число u, на второй и третий – с и s (u,v – компоненты двумерного вектора ![]() , тогда функционирование ВЭ можно описать следующим образом: на выход поступает u на ВР – v, где u и v определяются соотношениями
, тогда функционирование ВЭ можно описать следующим образом: на выход поступает u на ВР – v, где u и v определяются соотношениями ![]() ,
, ![]() .
.
Третий ВЭ. Он имеет два входа и один выход (обозначение ![]() ). На входы ВР поступают два числа: у и а, соответственно. На выход
). На входы ВР поступают два числа: у и а, соответственно. На выход ![]() .
.
Более подробное описание работы представленных ВЭ можно найти в [3–10].
Ниже на рис. 1 представлена систолическая структура, реализующая, описанный выше метод.
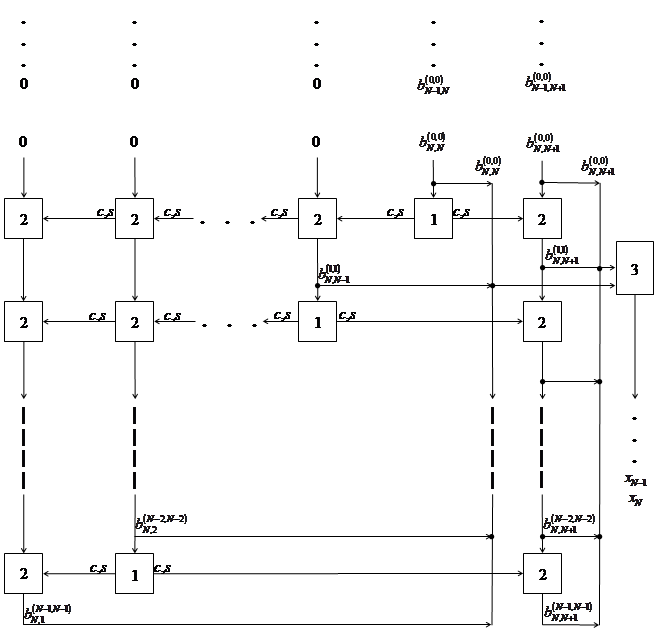
Рис. 1. Систолическая структура ортогонального обратного хода
Обсуждение результатов
После выполнения первого этапа система уравнений с верхней треугольной матрицей поступает на систолическую структуру, реализующую процедуру обратного хода (число обусловленности матрицы не вычисляется). Такой подход к решению системы уравнений может быть принятым, если априори известно, что решаемая система принадлежит классу невырожденных задач, а ее обусловленность позволяет получить приемлемое по точности решение.
Поскольку процедура обратного хода метода Гаусса ухудшает точность вычислений, выполнение второго этапа этим способом может привести к серьезному ухудшению точности полученного решения, особенно, если исходная задача имеет уже достаточно большое число обусловленности. Предлагаемый в статье метод обратного хода является методом трансформационного типа и поэтому свободен от этого недостатка и обеспечивает результату наибольшую точность.
Очевидно, если выход систолической системы Джентльмена-Кунга [1] соединить с входом представленной систолической структуры, то мы получим сквозной единый конвейер, работающий на частоте ![]() , где
, где ![]() – продолжительность операции сложения на сумматоре.
– продолжительность операции сложения на сумматоре.
Рецензенты:
Лебедев К.А., д.ф.-м.н., профессор кафедры вычислительной математики и информатики ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;
Уртенов М.А.Х., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.



