Постановка задачи. Среди задач об осесимметричном деформировании упругих оболочек вращения аналитическое решение допускают лишь простейшие – обычно относящиеся к оболочкам правильной формы [4]. Зачастую необходимо применение численных методов: конечно-разностных (и связанных с ними) или вариационных (методы Ритца, Бубнова-Галеркина, конечных элементов (МКЭ), вариационно-разностные). Наиболее распространенными являются вариационные методы, основанные на вариационном принципе Лагранже, в первую очередь – МКЭ [1]. Обычно они связаны с определением трех кинематических переменных: продольного и поперечного перемещений ![]() ,
, ![]() и угла поворота
и угла поворота ![]() . Возможно осуществить некоторое преобразование уравнений, при котором вместо
. Возможно осуществить некоторое преобразование уравнений, при котором вместо ![]() ,
, ![]() определяются радиальное и осевое перемещения
определяются радиальное и осевое перемещения ![]() ,
, ![]() . Это дает ряд преимуществ, в том числе: более простое описание геометрии, менее строгие требования к гладкости дуги меридиана, аддитивность переменных в нелинейной задаче и др. Порядок системы, однако, при этом не изменяется. В то же время в статически-определимых задачах, когда несамоуравновешенная нагрузка априорно известна, удается выразить осевой усилие через известные величины, получить системы 4-го порядка относительно
. Это дает ряд преимуществ, в том числе: более простое описание геометрии, менее строгие требования к гладкости дуги меридиана, аддитивность переменных в нелинейной задаче и др. Порядок системы, однако, при этом не изменяется. В то же время в статически-определимых задачах, когда несамоуравновешенная нагрузка априорно известна, удается выразить осевой усилие через известные величины, получить системы 4-го порядка относительно ![]() ,
, ![]() и отдельно формулу для
и отдельно формулу для ![]() (подобный прием используется при выводе уравнений Мейснера [4]).Полученная система, как и исходная система уравнений, обладает всеми необходимыми свойствами, чтобы сформулировать эквивалентный ей вариационный принцип. Любой вариационный метод, основанный на нем, приводит к разрешающей алгебраической системе меньшей размерности, что позволяет существенно уменьшить вычислительные затраты. Такой подход применим фактически к любому корректному варианту теории оболочек: классическому (типа Лява [4]), с учетом сдвига (типа Тимошенко) [2], [3] поперечного обжатия и перекрестных слагаемых в соотношениях упругости, для оболочек сложной внутренней структуры [5], анизотропных и т.д. Конкретная реализация ниже осуществлена на примере простейших уравнений типа Тимошенко.
(подобный прием используется при выводе уравнений Мейснера [4]).Полученная система, как и исходная система уравнений, обладает всеми необходимыми свойствами, чтобы сформулировать эквивалентный ей вариационный принцип. Любой вариационный метод, основанный на нем, приводит к разрешающей алгебраической системе меньшей размерности, что позволяет существенно уменьшить вычислительные затраты. Такой подход применим фактически к любому корректному варианту теории оболочек: классическому (типа Лява [4]), с учетом сдвига (типа Тимошенко) [2], [3] поперечного обжатия и перекрестных слагаемых в соотношениях упругости, для оболочек сложной внутренней структуры [5], анизотропных и т.д. Конкретная реализация ниже осуществлена на примере простейших уравнений типа Тимошенко.
Вывод вариационного уравнения
Запишем в наиболее общем матричном виде уравнения осесимметричного деформирования оболочки вращения, согласующиеся с любым вариантом теории:
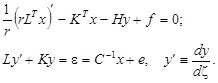 (1)
(1)
Здесь ![]() – радиус и меридиональная координата;
– радиус и меридиональная координата; ![]() – векторы обобщенных усилий, перемещений и деформаций;
– векторы обобщенных усилий, перемещений и деформаций; ![]() – векторы распределенных нагрузок и навязанных деформаций (вызванных, например, начальными напряжениями);
– векторы распределенных нагрузок и навязанных деформаций (вызванных, например, начальными напряжениями); ![]() – матрица жесткости;
– матрица жесткости; ![]() – матрица присоединенной жесткости (при наличии упругого подвеса);
– матрица присоединенной жесткости (при наличии упругого подвеса);![]() – некоторые геометрические матрицы. Символ
– некоторые геометрические матрицы. Символ ![]() означает транспонирование. Будем считать, что на краях заданы нулевые кинематические граничные условия или для некоторых компонент в общем случае – ненулевые граничные условия:
означает транспонирование. Будем считать, что на краях заданы нулевые кинематические граничные условия или для некоторых компонент в общем случае – ненулевые граничные условия:
![]() (2)
(2)
Системе (1) совместно с граничными условиями (2) соответствует вариационный принцип Лагранжа, который формулируется следующим образом. Среди всех векторов ![]() , удовлетворяющих кинематическим граничным условиям, решением задачи является тот, который доставляет функционалу
, удовлетворяющих кинематическим граничным условиям, решением задачи является тот, который доставляет функционалу ![]() минимальное значение:
минимальное значение:
![]() (3)
(3)
где
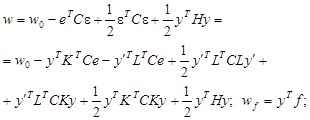 (4)
(4)
![]() – (5)
– (5)
удельная внутренняя энергия, удельная работа распределенной нагрузки, работа краевых сил. Слагаемое ![]() в формуле для
в формуле для ![]() является постоянным и может быть исключено из рассмотрения. Выражение под знаком интеграла в (3) может быть переписано в виде:
является постоянным и может быть исключено из рассмотрения. Выражение под знаком интеграла в (3) может быть переписано в виде:
![]()
где
![]() (6)
(6)
Конкретизируем вид матриц для простейших уравнений типа Тимошенко. Предварительно введем обозначения для недостающих геометрических, а также физических характеристик: ![]() – осевая координата;
– осевая координата; ![]() – угол между ортами
– угол между ортами ![]() и
и ![]()
![]() ;
; ![]() – радиусы меридиональной и широтной кривизн;
– радиусы меридиональной и широтной кривизн; ![]() – толщина;
– толщина; ![]() – модуль Юнга;
– модуль Юнга;![]() – коэффициент Пуассона. Будем считать, что заданы продольная, поперечная и моментная распределенные нагрузки
– коэффициент Пуассона. Будем считать, что заданы продольная, поперечная и моментная распределенные нагрузки ![]() , полная осевая сила
, полная осевая сила ![]() на краю
на краю![]() и, возможно, другие краевые усилия. Неизвестными являются меридиональные и окружные растягивающие усилия
и, возможно, другие краевые усилия. Неизвестными являются меридиональные и окружные растягивающие усилия ![]() и изгибающие моменты
и изгибающие моменты ![]() , соответствующие им деформации растяжения
, соответствующие им деформации растяжения![]() и изгиба
и изгиба ![]() , перерезывающее усилие
, перерезывающее усилие ![]() , сдвиг
, сдвиг ![]() , перемещения
, перемещения ![]() , поворот
, поворот ![]() . Они подчиняются известным уравнениям [2], для которых матрицы и векторы, входящие в (1), равны
. Они подчиняются известным уравнениям [2], для которых матрицы и векторы, входящие в (1), равны
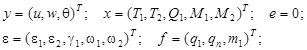
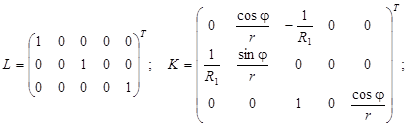
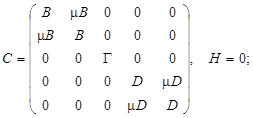 (7)
(7)
![]() (8)
(8)
Традиционное вариационное уравнение вытекает из (3), где использованы формулы (5), (6) и, согласно (7), вычислено
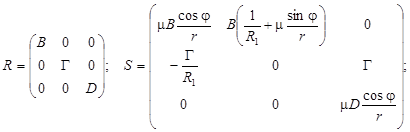 (9)
(9)
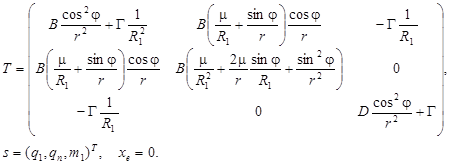
Для построения уравнений пониженной размерности введем осевые и меридиональные усилия, перемещения и внешние распределенные нагрузки:
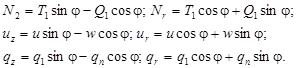 (10)
(10)
Это позволяет записать два уравнения равновесия:
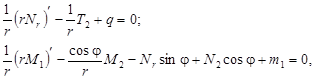
а из третьего уравнения
![]()
и условия ![]() вычислить осевое усилие
вычислить осевое усилие
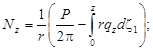 (11)
(11)
в простейшем случае, при ![]()
![]()
Далее, свяжем новые перемещения с компонентами деформаций:
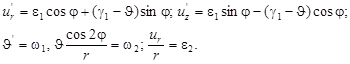
Наконец, соотношения упругости перепишем в виде
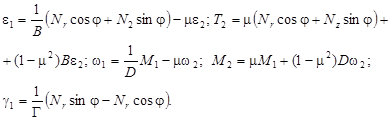
Подставив в уравнения равновесия и в выражения для производных от перемещений все выписанные формулы, получим систему уравнений относительно двух усилий и двух перемещений:
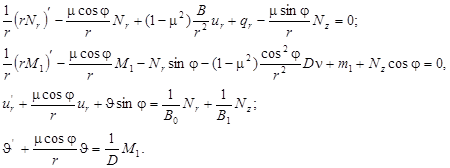 (12)
(12)
и отдельно формулу для перемещения ![]() (для определенности будем считать, что
(для определенности будем считать, что ![]() ), выраженного через них
), выраженного через них
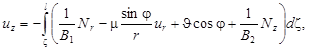 (13)
(13)
где обозначено
![]() (14)
(14)
Система (12) записывается в виде (1) при
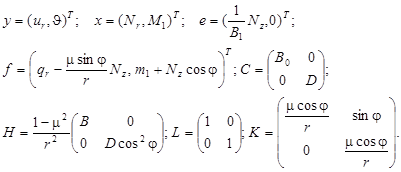 (15)
(15)
Следовательно, ей соответствует вариационный принцип (3), в котором использованы формулы (5), (6), и, согласно (15), вычислено
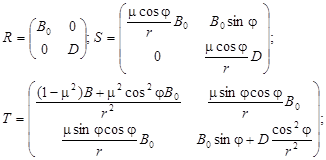
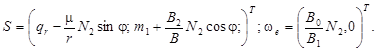 (16)
(16)
Обсуждение результатов и выводы
Таким образом, задача об осесимметричном деформировании оболочки вращения свелась к модифицированному вариационному уравнению, имеющему ту же структуру, что и традиционное, но пониженную размерность. Отметим условный характер присущих ему понятий: внутренняя энергия, упругий подвес и т.д. – которые в данном случае являются характеристиками уравнений, но не исходной конструкции как таковой. Подчеркнем, что например, при использовании традиционного метода конечных элементов с переменными ![]() исключение узловых значений
исключение узловых значений ![]() не позволяет прийти к модифицированным конечно-элементным уравнениям. Наконец, укажем ряд дополнительных преимуществ полученного модифицированного уравнения, кроме тех, которые связаны с выбором переменных в неподвижных осях (они указаны в начале статьи) и пониженной размерности. К ним относится значительно лучшая обусловленность матриц и возможность непрерывного перехода к теории типа Лява, связанная с тем фактом, что все компоненты матриц остаются конечными при
не позволяет прийти к модифицированным конечно-элементным уравнениям. Наконец, укажем ряд дополнительных преимуществ полученного модифицированного уравнения, кроме тех, которые связаны с выбором переменных в неподвижных осях (они указаны в начале статьи) и пониженной размерности. К ним относится значительно лучшая обусловленность матриц и возможность непрерывного перехода к теории типа Лява, связанная с тем фактом, что все компоненты матриц остаются конечными при ![]() (кроме тех точек, где
(кроме тех точек, где ![]() ).
).
Рецензенты:
Картузов Е.И., д.т.н., профессор кафедры теоретической механики Санкт-Петербургского Государственного морского технического университета, г. Санкт-Петербург;
Сорокин С.В., д.т.н., профессор кафедры сопротивления материалов Санкт-Петербургского Государственного морского технического университета, г. Санкт-Петербург.



