Ярким отражением математизации наук, т. е. процесса проникновения идей и методов математики в самые различные области знания, стала междисциплинарная интеграция математики и естественных, технических, экономических и других наук.
Как и у каждой науки, у математики славное прошлое и замечательное будущее. Научные исследования в области физики, химии, биологии, экологии, социологии, экономики, психологии и многих других наук не обходятся без применения математических методов. Поэтому большое значение для будущего специалиста в той или иной сфере деятельности имеет наличие у него исследовательской компетентности в области приложения математики.
Между школьной и высшей математикой имеется большая пропасть. К сожалению, в настоящее время в российском образовании все обучение математике и его содержание в первую очередь нацелено на подготовку к ЕГЭ. Цели обучения математике разнообразны. В них представлены такие направления, как развитие и воспитание личности учащегося в соответствии с потребностями общества, умение применять математические методы для практических нужд, подготовка для продолжения обучения в магистратуре и аспирантуре, в том числе по педагогическим и по физико-математическим специальностям. Взгляды на содержание обучения у разных педагогов могут сильно отличаться.
Изучение в вузе курса математики является важнейшим средством в решении проблемы формирования целостного научного мировоззрения молодых специалистов. Научное мировоззрение является системой взглядов на природу и общественные явления, основанной на данных науки. Работа преподавателей по формированию целостного научного мировоззрения у студентов должна быть направлена как на вооружение их научным пониманием окружающей действительности, так и на превращение этих знаний во внутренние убеждения каждого студента. Математика в процессе обучения студентов несет значительную мировоззренческую нагрузку: абстрактность математики и ее дедуктивный метод исследования позволяют один и тот же математический результат, одни и те же математические понятия применять к изучению самых разнообразных по своему конкретному содержанию явлений [1].
Рассмотрим вузовскую математику. Студенты математических специальностей изучают математику, подразделяя ее на алгебру, геометрию и математический анализ.
В течение всей своей трехвековой истории математический анализ занимал в математике ведущее положение. Его методами решали труднейшие практические задачи, он был объектом бесчисленных теоретических исследований. Именно средствами математического анализа строятся математические модели и производятся операции над этими моделями (дифференциальное и интегральное исчисление).
Попытки ввести начальные сведения из математического анализа в практику школьного математического образования предпринимаются издавна и ведутся с возрастающей настойчивостью. Часто бывает очень трудно разъяснить смысл вводимых понятий и операций и формализовать представление о рассматриваемом понятии, например о бесконечно малых величинах или понятии предела, с которым невозможно связать никакой регулярный алгоритм его вычисления. Понятие предела принципиально неалгоритмично, но оно оказывается основным в математическом анализе и широко используется при вычислениях.
В конце XVIII – начале XIX вв. возникла новая область научных знаний – дифференциальная геометрия, которая обосновывает приложение анализа к геометрии. Основателями этой области стали Л. Эйлер и его предшественники. Эйлер рассматривал выделение вопросов дифференциальной геометрии с двух точек зрения: первая связана с формированием математического анализа и рассмотрением его приложений к геометрии, а вторая – с решением задач картографии и геодезии (т.е. с потребностями практики). Основные результаты, полученные Эйлером в этой области, можно разделить на три группы:
1) результаты по теории кривых на плоскости;
2) результаты по теории кривых в пространстве;
3) результаты по теории поверхностей [2].
Ученики и последователи Эйлера стали прекрасными преподавателями математики, организаторами математического образования в России, авторами руководств по различным вопросам математики (в том числе и по приложениям дифференциального исчисления к геометрии), в которых были реализованы его основные методические идеи.
Первая из них – идея сближения содержания математического образования с современной математикой. Начиная с Л. Эйлера, в учебные курсы математики оперативно стали включаться новейшие достижения науки. Многие из его классических математических сочинений, например по приложению дифференциального исчисления к геометрии, были написаны столь доходчиво и живо, что в течение длительного времени использовались в качестве учебных руководств для университетов. Заложенная им традиция патронажа математики как науки над соответствующим учебным курсом обеспечивала научно-содержательные условия эффективного развития математического образования.
Вначале дифференциальная геометрия была составной частью учебного курса «Математический анализ». В настоящее время это отдельная дисциплина, которая читается студентам направлений подготовки «Математика» и «Математика и компьютерные науки».
Одним из разделов геометрии является многомерная геометрия, которая позволяет от геометрии плоскости и трехмерного пространства перейти к п-мерной евклидовой геометрии. Поэтому важно включать разделы многомерной геометрии в перечень курсов по выбору для подготовки квалифицированных специалистов-бакалавров по направлению «Математика».
Вторая идея – вычленение в математическом образовании основных дисциплин – арифметики, геометрии, тригонометрии, алгебры, математического анализа. Это привело к доминированию тенденции разумной минимизации количества математических дисциплин и избавлению от полиструктурности учебных математических курсов. В русле этой идеи идет их постепенное очищение от чужеродного материала.
Третья идея – построение учебных курсов по математике на основе прогрессивных для того времени таких дидактических принципов, как системность, научность, доступность изложения материала, учет возрастных особенностей учащихся.
Рассмотрим учебные планы направления подготовки «Математика». В этих планах присутствуют связные дисциплины: математический анализ и геометрия. В целях этих дисциплин просматривается «формирование систематических знаний в области математического анализа (дифференциальной геометрии и топологии), о его месте и роли в системе математических наук, приложениях в естественных науках» [5].
Компетенции, формируемые в результате изучения этих дисциплин:
1) общекультурные (ОК):
а) фундаментальная подготовка в области фундаментальной математики и компьютерных наук, готовность к использованию полученных знаний в профессиональной деятельности (ОК-11);
б) способность к анализу и синтезу информации, полученной из любых источников (ОК-14);
2) профессиональные (ПК):
а) глубокое понимание сути точности фундаментального знания (ПК-13);
б) выделение главных смысловых аспектов в доказательствах (ПК-16) [5].
Как видим, обе дисциплины ориентируют на учебно-воспитательный и научно-методический виды профессиональной деятельности, их изучение способствует решению типовых задач профессиональной деятельности.
Дифференциальная геометрия изучает линии и поверхности в трехмерном пространстве методами дифференциального и интегрального исчисления, т.е. с использованием таких понятий, как «производная», «дифференциал», «интеграл». Другими словами, основой дифференциальной геометрии являются:
1) аналитическая геометрия;
2) линейная (векторная) алгебра;
3) математический анализ.
Поэтому преподавателю, читающему дисциплину «Математический анализ», важно знать структуру дисциплины, умело выделяя в разделах основные, базовые понятия.
Преподавание дифференциальной геометрии и топологии создает базу для изучения алгебры, геометрии и математического анализа, предполагает достаточно хорошее освоение классических результатов вышеперечисленных предметов. В то же время нельзя изучить дифференциальную геометрию, не изучив математический анализ, который является основой всей вузовской математики.
Организуя учебные занятия по дисциплинам профиля, нужно учитывать их порядок, последовательность, отражать научно-методические основы дисциплины. Аудиторная работа включает лекции, практические занятия, самостоятельную работу, творческие индивидуальные задания.
Рассмотрим пример. Хорошо прослеживается связь между математическими дисциплинами при изучении раздела «Дифференциальное и интегральное исчисление», который является основой всей математики. Этот раздел изучается не только студентами-педагогами, но и в большей степени он необходим студентам технических вузов и прикладных направлений подготовки.
В курсе математического анализа решаются геометрические задачи на нахождение наибольших и наименьших значений величин. В обязательной программе это не выделяется ни в алгебре, ни в геометрии, хотя его большая роль в формировании ряда личностных качеств студента и его мировоззрения неоспорима. Этот курс углубляет знания студентов по математике, способствует повышению качества их математической подготовки, ярче и глубже отражает достижения и проблемы современной математики, содействует профессиональной ориентации студентов в области математики. При этом необходимо дать будущему учителю возможность познакомиться с интереснейшими задачами и их решениями по истории математики, помочь в приобретении навыков решения геометрических задач не только с применением производной, но и методами элементарной математики.
Покажем на конкретном примере связь между указанными дисциплинами. Рассмотрим вариант лекции [3]. В курсе математического анализа изучаются частные производные и их геометрический смысл. Показывается, что касательная плоскость имеет уравнение вида: 
. Если уравнение поверхности задано в виде 
, то уравнение касательной плоскости примет вид: 
. Нормаль к поверхности имеет вид: 
, а если уравнение поверхности задано в виде, то 
.
В дифференциальной же геометрии пространственную кривую можно задать и параметрическими уравнениями 
или векторным уравнением 
. Это уравнение задает 
как вектор-функцию скалярного аргумента 
, т.е. 
Соответствующую кривую называют годографом вектора .
Уравнения касательной к кривой 
в точке 
имеют вид: 
, где 
— производные функций 
в точке 
.
Как видим, между математическим анализом и геометрией есть много общего. И студентам необходимо показывать эту связь как можно чаще.
Покажем еще на одном примере. Рассмотрим дугу кривой без кратных и особых точек, заданную параметрическими уравнениями: 
и 
. Если в каждой точке провести касательную, то вследствие того, что дуга искривлена, эта касательная с перемещением точки касания будет вращаться. Степень искривленности (или кривизну) в различных точках можно выразить некоторым числом.
Кривизной кривой в точке М назовем предел, к которому стремится средняя кривизна дуги ММ1, когда точка М1 вдоль по кривой стремится к М.
Кривизна окружности есть величина, обратная радиусу окружности 
, так как 
.
Формула для вычисления кривизны кривой: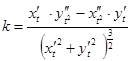 
. Если кривая задана явным уравнением 
, тогда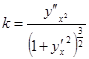 
, если же полярным уравнением, то ее кривизна: 
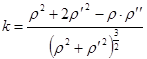. Радиус кривизны вычисляется по формуле: 
.
Так, в курсе математического анализа рассматриваются кривые, исследуются графики функций на выпуклость, которая определяется с помощью второй производной. Поэтому предполагается, что студенты должны знать основные понятия. В этом случае сразу можно подвести студентов к тому, что есть такое понятие, как «кривизна кривой (изгиб)».
В дифференциальной геометрии рассматривается в пространстве линия 
, отнесенная к натуральному параметру s. Линия имеет уравнение: 
.
В каждой точке М линии определены три взаимно-перпендикулярные прямые: касательная, главная нормаль и бинормаль. При движении точки М по линии эти три прямые вращаются с некоторой скоростью, зависящей от самой линии . Скорость вращения касательной 
называется кривизной линии в точке М и обозначается 
, а скорость вращения бинормали называется кручением линии в точке М и обозначается 
.
В векторной форме кривизна вычисляется по формуле: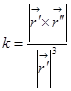 
. Кручение 
.
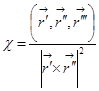Практические занятия в учебном процессе имеют, наверное, большее значение, чем лекции. Основная цель этих занятий – отработка теоретического материала, формирование умений по применению теоретических знаний на практике. Они являются наиболее активной формой общения с преподавателем. На этих занятиях закрепляется изученный на лекциях материал, решаются конкретные задачи. В начале практических занятий рекомендуется проведение небольшой проверочной работы, например математического диктанта по знанию основных определений, теоретических фактов, формул, необходимых на данном занятии.
Большое значение имеет и самостоятельная деятельность студентов, формы которой необходимо продумать заранее и нацеливать на ее выполнение с первых занятий.
Задачи, показывающие связь между математическим анализом и геометрией, приучают студентов логически рассуждать, развивают умения анализировать, синтезировать, конкретизировать, обобщать, т.е. способствуют развитию логического мышления и пространственных представлений у обучаемых, строгости суждения, графической культуры. Эти задачи заставляют студентов обстоятельнее и глубже разобраться в известных им сведениях как по математическому анализу, так и по геометрии, а также побуждают дать им практическое применение.
Самостоятельным творческим исследованием является написание курсовых работ. Работа со специальной литературой позволяет развивать творческий потенциал, познавательный интерес, интеллектуальную инициативу, умение самостоятельно ориентироваться в обширной научной литературе. Это также способствует освоению студентами логики и методологии научного поиска, что является обязательным компонентом общенаучной и инструментальной компетенций.
Например, рассмотрим тему курсовой работы «Элементы многомерной геометрии».
Цель данной работы: рассмотреть подробно аксиоматику Вейля многомерного евклидова пространства на базе линейной алгебры.
План
1. Рассмотреть основные факты линейной алгебры.
2. Дать построение многомерного евклидова пространства.
3. Изучить плоскости произвольных размерностей в многомерном евклидовом пространстве.
Также предлагается литература для написания курсовой работы.
Даже по указанной теме можно проследить связь между математическими дисциплинами.
По аналогичной теме может быть предложена и выпускная квалификационная работа.
Рецензенты:
Егорова Г.И., д.п.н., профессор, заведующая кафедрой химии и химической технологии федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Тюменский государственный нефтегазовый университет» филиал в г. Тобольске, г. Тобольск.
Маллабоев У., д.ф.-м.н., профессор кафедры физики, математики и методик преподавания федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Тюменский государственный университет» филиал в г. Тобольске, г. Тобольск.