Основной целью высшего образования становится подготовка выпускника не просто знающего, но умеющего распорядиться этим знанием, то есть подготовка профессионала, обладающего критическим мышлением, способного среди множества решений выбирать наиболее оптимальное, аргументировано опровергая ложные; профессионала, готового к самообразованию, самоопределению, саморазвитию [4].
Стремительно меняющиеся требования к выпускнику вуза, большой объем информации, необходимой для усвоения к концу обучения, вынуждают использовать в вузовском образовании различные методы активного обучения [1,2,3]. Активные методы обучения – методы, стимулирующие познавательную деятельность обучающихся, они строятся в основном на диалоге, предполагающем свободный обмен мнениями о путях разрешения той или иной проблемы, характеризуются высоким уровнем активности студентов и способствуют развитию у них элементов критического мышления.
Именно такое обучение сейчас общепринято считать «наилучшей практикой обучения» [5]. Исследования показывают, что именно на активных занятиях – если они ориентированы на достижение конкретных целей и хорошо организованы – учащиеся часто усваивают материал наиболее полно и с пользой для себя.
В последнее время все большее число преподавателей приходит к пониманию необходимости перехода от репродуктивных методов преподавания к продуктивным, от передачи студентам готовых знаний к активному вовлечению их в учебно-познавательную деятельность по конструированию новых знаний.
Необходимость совершенствования образовательной деятельности в вузе отражена в Федеральных государственных образовательных стандартах третьего поколения. Предлагается «…широкое использование в учебном процессе активных и интерактивных форм проведения занятий (компьютерные симуляции, деловые и ролевые игры, разбор конкретных ситуаций, психологические и иные тренинги) в сочетании с внеаудиторной работой с целью формирования и развития профессиональных навыков обучающихся» [11]. Таким образом, перед преподавателями высшей школы ставятся вполне конкретные задачи – перевести часть занятий, ранее осуществлявшихся в традиционной форме, в активные. В связи с этим каждого преподавателя вуза сейчас волнуют вопросы, связанные с необходимостью самостоятельно разрабатывать свои занятия в активных формах с учетом специфики учебного курса в рамках той или иной специальности [7,8,9].
Рассмотрим возможности организации занятий в активных формах на примере изучения темы «Элементы теории множеств» в рамках учебной дисциплины «Математика» для студентов направлений «Начальное образование» и «Начальное и дошкольное образование».
Как известно, готовность к деятельности является первичным фундаментальным условием ее успешного выполнения [12]. Одним из основных факторов, определяющих готовность студентов к изучению новой темы, является наличие у них устойчивой мотивации предстоящей учебно-познавательной деятельности. Основное назначение этого этапа заключается в формировании у каждого студента личной потребности в последующей деятельности, связанной с открытием субъективно нового для него содержания [6,10]. Эффективными методическими приемами, которые могут быть использованы на данном этапе, как показала практика, являются работа с ключевыми понятиями, работа с утверждениями (либо с вопросами).
В первом случае, в начале занятия студентам предлагается ряд ключевых понятий новой темы: множество, элемент множества, конечные и бесконечные множества, пустое множество, способы задания множеств, отношения между множествами, операции над множествами. Каждое понятие необходимо охарактеризовать и попытаться сформулировать соответствующее определение. Работа может быть организована в форме коллективной дискуссии, либо студенческая группа разбивается на подгруппы по 4–5 человек, в каждой из которых ведется обсуждение с последующей комментированной защитой своего мнения. В случае ограниченности во времени стадия обсуждения может быть пропущена, и после рассмотрения ключевых понятий можно сразу переходить к следующему этапу – этапу непосредственного получения новой информации.
Во втором случае, перед изучением темы студентам предлагается ряд утверждений, которые необходимо оценить с позиции «истинно» – «ложно»:
1. Множество действительных корней уравнения ![]() есть
есть
а) конечное множество, б) бесконечное множество, в) пустое множество.
2. Если ![]() ,
, ![]() , то
, то
а) А![]() В,
В,
б) В![]() А,
А,
в) А=В.
3. Если А![]() В, В
В, В![]() С, то А
С, то А![]() С.
С.
4. Если Х – множество двузначных чисел, У – множество четных чисел, то
а) 21 Є К∩М;
б) 32 Є К ∩ М;
в) 32 Є К U М;
г) 7 Є К ∩ М;
д) 7 Є К U М;
е) 135 Є К U М.
5. Если А = {x / x![]() N, x< 5}, B = {x / x
N, x< 5}, B = {x / x![]() N, x> 7}, то
N, x> 7}, то
а)А U В= {x / x![]() N, x< 5},
N, x< 5},
б) А ∩ В=Ø,
в) А \ В={x / x![]() N, x< 5},
N, x< 5},
г) В \ А= Ø
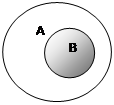
6. На диаграмме Эйлера – Венна закрашенная область соответствует разности множеств В и А.
Третий вариант отличается от второго формулировкой заданий:
1. А – множество многоугольников. Принадлежит ли этому множеству:
а) восьмиугольник;
б) отрезок;
в) параллелограмм;
г) параллелепипед;
д) круг;
е) полукруг?
2. Для каких из следующих пар множеств имеет место отношение
1) А![]() В,
В,
2) В![]() А,
А,
3) А=В:
а) А = {a, b, c, d}, B = {a, c, d};
б) А = {a, b}, B = {a, c, d};
в) А = Ø, В = Ø;
г) А = Ø, В = {a, b, c};
д) А = Ø, В = {Ø};
е) A = {{a}, a, Ø}, B = {a}?
3. В каком отношении находятся множества B и D, если:
а) B = [3; 5], D = [4; 6];
б) B = (7; ∞), D = [8; 12);
в) B = (-∞; 0], D = [0; 7];
г) B = (-5; -1), D = (-1; 6)?
4. Множество М есть объединение множества двузначных натуральных чисел и множества натуральных чисел от 1 до 7. Принадлежат ли множеству М числа 14, 99, 100, 5, 7, 10?
На данный момент студенты не обладают знаниями, необходимыми для ответа на все поставленные вопросы. Поэтому переход к следующему этапу – этапу непосредственного получения новой информации – приобретает для них особую значимость.
Изучение новой темы также может быть организовано разными способами. Если на начальной стадии были использованы описанные выше приемы, то усвоение новых знаний сопровождается поиском ответов на поставленные ранее вопросы, что способствует более осознанному усвоению информации.
На данном этапе может быть использован прием «чтения с пометками», который заключается в одновременном прочтении и анализе текста лекции. Результаты анализа могут быть зафиксированы на полях значками «+» (новая информация), «v» (известная информация), «-» (информация, противоречащая представлениям студента) и т.д.
Студентам могут быть выданы раздаточные материалы, содержащие теоретическую информацию, которую необходимо разделить по смысловым блокам. Результаты такого анализа целесообразно структурировать с использованием опорных материалов (таблиц, схем, рисунков и пр.). Применение графических форм в ходе усвоения математических знаний позволяет студентам наглядно представить изучаемый материал, сконцентрировать внимание на самом существенном, главном, глубже разобраться в новой информации и легче ее запомнить.
Формирование у студентов навыков самостоятельной работы с опорными материалами осуществляется поэтапно. Овладев методикой их составления, студенты смогут легко справляться с большими объемами информации, анализировать ее, группировать и классифицировать, устанавливать закономерности и делать самостоятельные выводы. Ниже приведен пример опорного конспекта, который может быть использован при изучении темы «Элементы теории множеств» (рисунок).
Перестройка полученных студентами знаний, приспособление их к решению задач осуществляются на этапе закрепления полученных знаний. Прежде чем в сознании студента возникнут устойчивые интеллектуальные структуры, необходимо активно поработать с элементами учебного материала. С этой целью студентам может быть предложено задание на составление вопросов и заданий по изученной теме. Студенты объединяются в группы, каждая из которых выбирает один их блоков информации (например, понятие и виды множеств, отношения между множествами, операции над множествами) и составляет вопросы и задания на воспроизведение и понимание информации. Далее, в ходе взаимного опроса, полученные знания студентов уточняются и расширяются.
Совершенствование содержания, усвоенного на предыдущих этапах обучения, осуществляется на этапе применения полученных знаний. Функциональное назначение данного этапа заключается в формировании умений и навыков решения задач на применение полученных знаний в различных учебных и практических ситуациях. Так, студентам может быть предложено задание заполнить таблицу на установление связей между основными понятиями теории множеств, изучаемыми в высшем и начальном курсе математики:
|
Основные понятия теории множеств |
Трактовка понятий в математике |
Трактовка понятий в начальном курсе математике |
Примеры заданий из учебников начального курса математики |
|
|
|
|
|
Организованная таким образом работа не только активизирует познавательную учебную деятельность студентов, но и способствует профессиональному становлению будущего учителя начальных классов.
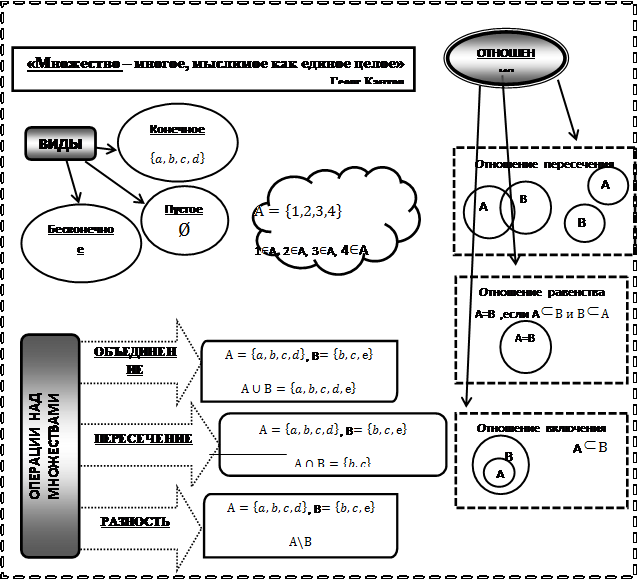
Опорный материал «Теория множеств»
Таким образом, активные формы работы студентов могут быть использованы на различных этапах усвоения студентами математических знаний. Целенаправленное и систематическое их применение в учебном процессе дает возможность создания продуктивной образовательной среды, способствующей развитию критического мышления студентов, стимулирующей их к самостоятельному приобретению новых знаний, предоставляющей возможность постоянного самообразования, самораскрытия и самореализации личности.
Рецензенты:
Вострокнутов И.Е., д.п.н., профессор кафедры физико-математического образования Арзамасского филиала Нижегородского государственного университета, г. Арзамас;
Фролов И.В., д.п.н., профессор, заведующий кафедрой физико-математического образования Арзамасского филиала Нижегородского государственного университета, г. Арзамас.



