В работе обосновывается и рассматривается вопрос об изменении последовательности в структуре изложения заявленной темы.
В традиционном курсе физики [5], а также в курсе физики с нетрадиционной схемой построения [6] обычно явления, связанные с волновыми процессами (интерференция, дифракция, поляризация), рассматриваются для конкретных примеров. При этом глубокая логика рассматриваемых явлений не всегда выявляется. Например, в [6] раздел III «Волновые свойства фотонов» начинается с рассмотрения опыта Юнга, интерференции в тонких пленах, колец Ньютона.
Вероятно, методически более приемлемо вначале рассматривать общий подход к анализу подобных явлений, а затем перейти к отдельным примерам.
Интерференция световых волн – это явление перераспределения светового потока в пространстве при наложении когерентных колебаний одинакового направления, в результате чего в одних точках наблюдаются максимумы, а в других — минимумы интенсивности света.
Механические волны и электромагнитные волны описываются одинаковыми волновыми уравнениями, поэтому при описании явления интерференции волн любого вида можно использовать общий математический аппарат.
Основной задачей изучения волн является выяснение закона изменения во времени и пространстве физических величин, однозначно характеризующих тот или иной тип волнового движения. Зависимость такой физической величины (введем в общем случае обозначение ξ) от пространственных координат и времени (![]() ) называется уравнением волны. Простейшим типом волн являются синусоидальные (гармонические) волны, при которых для всех точек среды, охваченной волновым процессом (движением), значения колеблющейся физической величины изменяются по гармоническому закону с одинаковой частотой ω.
) называется уравнением волны. Простейшим типом волн являются синусоидальные (гармонические) волны, при которых для всех точек среды, охваченной волновым процессом (движением), значения колеблющейся физической величины изменяются по гармоническому закону с одинаковой частотой ω.
В общем случае, например, для плоских волн (волновые поверхности имеют вид плоскостей, параллельных некоторой плоскости CD и перпендикулярных направлению распространения волны), распространяющихся вправо и влево от плоскости CD (от источника волн) вдоль оси X, уравнения волн имеют вид:
ξ = ![]() , (1)
, (1)
ξ = ![]() ,
,
где x0 – координата плоскости источника волн.![]()
Используя формулу Эйлера
![]() , (2)
, (2)
где ![]() – мнимая единица, уравнение плоской волны можно записать в следующем виде [7]:
– мнимая единица, уравнение плоской волны можно записать в следующем виде [7]:
![]() (3)
(3)
Здесь: ![]() — волновой вектор,
— волновой вектор, ![]() – радиус-вектор, определяющий положение рассматриваемой точки;
– радиус-вектор, определяющий положение рассматриваемой точки; ![]() – комплексная амплитуда волны.
– комплексная амплитуда волны.
![]() , (4)
, (4)
где: А — вещественная амплитуда волны; ![]() , α – начальная фаза колебаний в начале координат (т.е. в точке r = 0). В выражении (3) физический смысл имеет только вещественная часть, которую обозначают символом Re.
, α – начальная фаза колебаний в начале координат (т.е. в точке r = 0). В выражении (3) физический смысл имеет только вещественная часть, которую обозначают символом Re.
![]()
Используя выражение, подобное (3), например, для плоской волны, распространяющейся вдоль положительного направления оси OX, можно выполнить следующие математические операции.
![]() (5)
(5)
(При выводе выражения (5) принято во внимание, что (![]() ) = k∙x).
) = k∙x).
Отсюда
![]()
и, следовательно, вещественная (действительная) часть
![]()
![]() (6)
(6)
![]()
Расчет картины интерференции волн в линейных средах основан на принципе суперпозиции, согласно которому результирующее волновое поле, создаваемое несколькими источниками, равно сумме полей, создаваемых каждым из источников. Согласно принципу суперпозиции комплексная амплитуда результирующего поля равна сумме комплексных амплитуд всех интерферирующих волн.
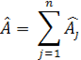 (7)
(7)
Рассмотрим явления, наблюдаемые при сложении волн от нескольких источников, колеблющихся с определенной фазой относительно друг друга.
Рассмотрим общий случай сложения распространяющихся в одном направлении монохроматических плоских световых волн с изменяющимися амплитудами и фазами. Запишем выражения для системы плоских монохроматических волн с одинаковыми частотами ![]() . Предположим, что амплитуда волн убывает от волны к волне с постоянным коэффициентом K (K<1), тогда можно записать:
. Предположим, что амплитуда волн убывает от волны к волне с постоянным коэффициентом K (K<1), тогда можно записать:
![]() (8)
(8)
…………………….
![]()
…………………….
![]()
Здесь: Ej – напряженность электрического поля световой волны в точке с координатой x в некоторый момент времени t; δ – разность фаз между волнами j и (j – 1) порядка; n – общее число интерферирующих волн; с = 3∙108 м/с – скорость света в вакууме (воздухе). (В общем случае E зависит от координат и от времени.)
Используя (8), согласно принципу суперпозиции запишем:
![]() (9)
(9)
Применяя преобразования записанной суммы, можно получить:
![]() (10)
(10)
(Соотношение (10) получено с использованием метода определения суммы n членов геометрической прогрессии в выражении (9), где знаменатель прогрессии ![]() .) Интенсивность I результирующей волны пропорциональна квадрату амплитуды E0 результирующих колебаний:
.) Интенсивность I результирующей волны пропорциональна квадрату амплитуды E0 результирующих колебаний: ![]() , (здесь
, (здесь ![]() — величина, комплексно сопряженная с E0).
— величина, комплексно сопряженная с E0).
Используя (10), запишем (принимая n→∞, как это часто реализуется на практике):
![]() или (11)
или (11)
![]()
Исследуя функцию (11) на экстремум, получим, что максимум ![]() и, соответственно, максимум интенсивности результирующей волны имеет место при значении δ = 2mπ, а минимум — при значении δ = (2m+1)π (где m = 0; 1; 2; …).
и, соответственно, максимум интенсивности результирующей волны имеет место при значении δ = 2mπ, а минимум — при значении δ = (2m+1)π (где m = 0; 1; 2; …).
Рассмотрим теперь сложение распространяющихся в одном направлении волн с одинаковыми амплитудами и частотами. В этом случае согласно принципу суперпозиции напряженность E результирующего поля световой волны определяется выражением:
![]() (12)
(12)
Используя преобразования записанной суммы, получим:
![]()
Интенсивность I результирующей волны пропорциональна квадрату амплитуды E0 результирующих колебаний:
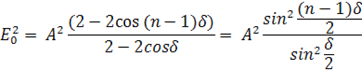 (13)
(13)
Следовательно, интенсивность в точках, соответствующих интерференционному максимуму, зависит от разности фаз δ. Условия для максимума и минимума интенсивности результирующей световой волны найдем, исследуя выражение (13) на экстремум.
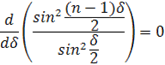 (14)
(14)
Проведем некоторые математические преобразования.
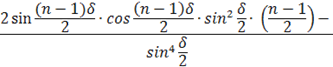 (15)
(15)
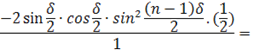
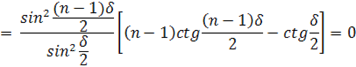
Из (15) условие для интерференционных максимумов определим исходя из равенства:
![]() (16)
(16)
Используя (16), выражение (13) можно представить в виде:
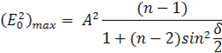 (17)
(17)
Главные максимумы возникают при значении ![]() , т.е. при
, т.е. при
![]() , (18)
, (18)
где порядок интерференционного максимума m = 0, 1, 2 …
Из выражения (15) условие минимума интенсивности в результате интерференции световых волн определим из равенства:
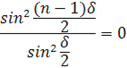 (19)
(19)
или
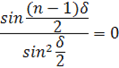
Условие интерференционных минимумов
![]() (20)
(20)
Здесь порядок интерференционного минимума m = 1, 2, 3, … , но m ≠ 0, n, 2n и т.д.
(При указанных значениях m получаем максимум функции (13), раскрыв неопределенность).
Анализируя условия (18) и (20), можно заключить, что между соседними главными максимумами (j-го и (j+1)-ого порядков) располагается (n – 1) минимум. И так как функция (13) непрерывна, то, кроме главных, будет еще (n – 2) побочных максимума. Положение побочных максимумов, интенсивность которых много меньше интенсивности главных максимумов, определяется следующим условием:
Разность фаз ![]() , где m’ – номер побочного максимума, отсчитанный от соответствующего главного максимума.
, где m’ – номер побочного максимума, отсчитанный от соответствующего главного максимума.
На рисунке представлен график функции (13) в случае интерференции волн с одинаковым частотами (график выполнен для значения n= 7).
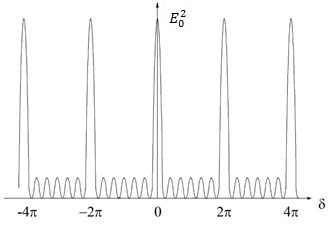
Результаты анализа сложения волн с одинаковыми амплитудами и частотами позволяют сделать следующие выводы:
1) положение главных максимумов не зависит от числа интерферирующих волн;
2) ширина главных максимумов ![]() убывает с увеличением числа n интерферирующих волн, при этом возрастают четкость и яркость интерференционной картины.
убывает с увеличением числа n интерферирующих волн, при этом возрастают четкость и яркость интерференционной картины.
Рассматривая общий случай сложения волн с закономерно изменяющимися амплитудами и фазами, мы получили выражение (11), в которое входит коэффициент K, характеризующий изменение амплитуд.
Если амплитуды интерферирующих волн убывают медленно (K ≈ 1), то согласно (11) в точках максимума интенсивность пропорциональна ![]() .
.
При K → 1 интенсивность возрастает, а картина интерференции волн будет иметь вид ярких узких полос на темном фоне.
Если K<<1, то амплитуда интерферирующих волн убывает быстро, и мы можем рассматривать практически интерференцию двух волн [4] .
![]()
Мы рассматриваем интерференционные явления, создаваемые источниками, которые возбуждают волны, находящиеся в фазе друг относительно друга, или волны с некоторым определенным соотношением фаз. Это когерентные источники.
Методы получения когерентных источников света известны [1, 3]. Например, когерентные источники света можно получить, если осветить одним точечным источником света два или более отверстия или несколько щелей. Кроме того, например, в интерферометре Майкельсона когерентные источники света создаются с помощью полупрозрачных зеркал. Если плечи интерферометра одинаковы, то в фокальной плоскости зрительной трубы будет наблюдаться четкая интерференционная картина. Но в случае, когда плечи интерферометра имеют разную длину, интерференционная картина может вообще исчезнуть, если разность хода лучей (примерно одинаковой интенсивности, которые распространяются после разделения пластинкой в разных «плечах» интерферометра, а затем снова встречаются) превысит некоторую величину ![]() , соответствующую разности времен
, соответствующую разности времен ![]() .
.
Величину ![]() называют длиной когерентности, а
называют длиной когерентности, а ![]() – временем когерентности.
– временем когерентности.
С помощью спектрометра высокой разрешающей способности можно проанализировать свет от источника в интерферометре и обнаружить четкую линию с шириной ![]() , которая связана с временем когерентности согласно [4], соотношением:
, которая связана с временем когерентности согласно [4], соотношением:
![]() (21)
(21)
Для источника монохроматического света (лазер, свечение атомов) полагают, что средняя частота излучения ![]() меняется в интервале от значения
меняется в интервале от значения ![]() до значения
до значения ![]() . Тогда в соответствии с (21) две синусоидальные волны, разнесенные по частоте на величину
. Тогда в соответствии с (21) две синусоидальные волны, разнесенные по частоте на величину ![]() , будут оставаться в фазе в течение времени
, будут оставаться в фазе в течение времени ![]() .
.
Наиболее узким линиям атомных спектров соответствует время когерентности ![]() с.
с.
Пространственная когерентность связана с конечными размерами реальных источников света. Например, из опытов по наблюдению интерференции света с использованием зеркал Френеля можно сделать следующие выводы.
Источник света S (в виде узкой щели) дает монохроматическое излучение. При отражении от двух зеркал падающая волна разбивается на две когерентные волны, которые интерферируют (получаем интерференционную картину в виде чередующихся светлых и темных полос).
Исчезновение интерференционной картины с увеличением ширины щели (полосы вначале уширяются, а потом вообще исчезают) связано с нарушением условия пространственной когерентности. Мнимые источники (мнимые изображения щели S в зеркалах 1 и 2) содержат множество светящихся точек, попарно когерентных, дающих на экране систему интерференционных полос, сдвинутых относительно друг друга.
Интерференционные полосы на экране исчезнут, когда максимумы одной интерференционной картины точно совпадут с минимумами другой. Тогда условие сохранения пространственной когерентности можно записать в виде ![]() . Здесь
. Здесь ![]() – сдвиг интерференционных полос, образованных источниками S1 и S2, относительно системы полос от соответствующих источников
– сдвиг интерференционных полос, образованных источниками S1 и S2, относительно системы полос от соответствующих источников ![]() ;
; ![]() – расстояние между соседними полосами, полученными от определенной пары когерентных источников.
– расстояние между соседними полосами, полученными от определенной пары когерентных источников.
Например, используя известные методы расчета интерференционных картин (в расположении Юнга, в опытах с зеркалами Френеля и бипризмой Френеля) [1, 2, 7], запишем известное соотношение ![]() λ, где L – расстояние от источников (мнимых) до экрана наблюдения; d – расстояние между источниками; λ – длина волны монохроматического излучения.
λ, где L – расстояние от источников (мнимых) до экрана наблюдения; d – расстояние между источниками; λ – длина волны монохроматического излучения.
Введя угол α – угол, под которым видны когерентные источники света из точки, где наблюдается интерференция, примем ввиду малости этого угла, что ![]() . Если рассматривать распределение интенсивности света на экране, полученное от крайних точек щели, сдвиг кривых Δy равен ширине щели b. Тогда можно получить условие пространственной когерентности в виде b∙α << λ.
. Если рассматривать распределение интенсивности света на экране, полученное от крайних точек щели, сдвиг кривых Δy равен ширине щели b. Тогда можно получить условие пространственной когерентности в виде b∙α << λ.
При выборе требуемых условий для наблюдения интерференции света нужно учесть, что увеличение яркости интерференционных полос за счет увеличения размеров источника (ширина щели b) приводит к уменьшению размеров интерференционного поля.
Сравним интерференционную картину в случае двухлучевой интерференции и в случае многолучевой интерференции.
Оценим характер интерференционной картины в случае наложения большого числа когерентных волн. Для ее наблюдения применяются специальные интерференционные приборы – эталон Фабри—Перо, пластинка Люммера—Герке, дифракционная решетка.
При падении, например, на эталон Фабри—Перо расходящегося пучка монохроматического света от источника на экране наблюдается система интерференционных полос (колец) равного наклона. Имеет место усиление всех интерферирующих волн, приходящих в точки экрана в одинаковой фазе. Результирующая амплитуда в интерференционных максимумах
![]() ,
,
где: ![]() – амплитуда j –той волны, N – число интерферирующих волн.
– амплитуда j –той волны, N – число интерферирующих волн.
Интерференционные максимумы оказываются значительно более узкими и яркими, чем в случае двухлучевой интерференции. Например, при интерференции волн с одинаковыми амплитудами A0 запишем ![]() .
.
Энергия результирующих колебаний и освещенность экрана в области интерференционных максимумов пропорциональны квадрату числа интерферирующих волн; суммарная энергия этих волн пропорциональна ![]() , т.е. числу интерферирующих волн.
, т.е. числу интерферирующих волн.
Общая энергия колебаний во всех точках экрана пропорциональна N, так как по закону сохранения и превращения энергии она должна равняться суммарной энергии всех N интерферирующих волн. Таким образом, возрастание яркости интерференционных максимумов с увеличением числа N интерферирующих волн должно сопровождаться их одновременным сужением и соответствующим расширением площади слабо освещенных участков картины.
Рецензенты:
Румбешта Е.А., д.п.н., профессор, кафедра физики Томского государственного педагогического университета, г. Томск;
Улеников О.Н., д.ф.-м.н., профессор, кафедра теоретической физики Томского государственного университета, г. Томск.



