В работе проводится исследование краевой задачи со свободными границами, описывающей динамику температурного поля при деструкции тканей плоскопараллельными аппликаторами. Рассмотрена задача криодеструкции, когда присутствует замороженная область и определению подлежат функция ![]() , и неизвестные границы
, и неизвестные границы ![]() . Для решения задачи в работе применяются методы нелинейных интегральных, интегро-дифференциальных уравнений, метод Ротэ, метод эквивалентной линеаризации, а также проведена конечномерная аппроксимация.
. Для решения задачи в работе применяются методы нелинейных интегральных, интегро-дифференциальных уравнений, метод Ротэ, метод эквивалентной линеаризации, а также проведена конечномерная аппроксимация.
Получено точное аналитическое решение соответствующей стационарной задачи, которое определяет очень важные для хирурга максимальные размеры замораживания, криопоражения и теплового возмущения.
Конечномерной аппроксимацией решение полученной системы сведено к решению системы нелинейных алгебраических уравнений.
1. Постановка задачи
В различных областях медицины при деструкции тканей применяются достаточно протяженные плоские аппликаторы. Определение динамики температурного поля в этом случае сводится к решению следующей задачи со свободными границами для нелинейных эволюционных уравнений [1, 2, 6]:
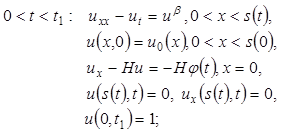 (1)
(1)
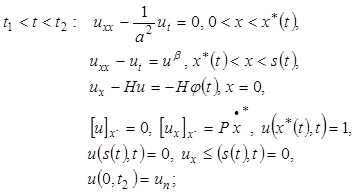 (2)
(2)
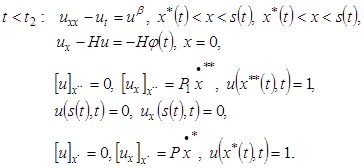 (3)
(3)
В задаче (1)–(3) искомыми являются температурное поле ![]() и границы
и границы ![]() остальные параметры и функции известные,
остальные параметры и функции известные, ![]() .
.
Аналитическое решение стационарной задачи (1)–(3) имеет вид [6]:
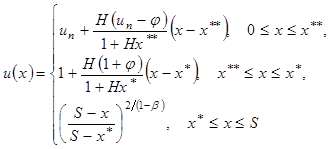 (4)
(4)
где
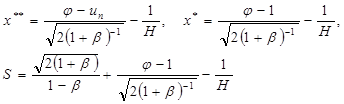 (5)
(5)
2. Задача криодеструкции биологической ткани
Если ![]() , то при
, то при ![]() будет возникать замороженная область биоткани
будет возникать замороженная область биоткани ![]() . В этом случае метод Ротэ для задачи (1)–(3) приводит к системе краевых задач со свободными границами
. В этом случае метод Ротэ для задачи (1)–(3) приводит к системе краевых задач со свободными границами ![]() и
и ![]() :
:
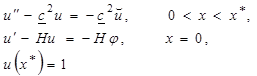 (6)
(6)
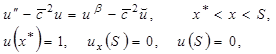 (7)
(7)
![]() . (8)
. (8)
С помощью функций Грина ![]() и
и ![]()
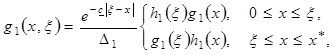 (9)
(9)
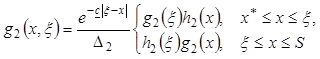
определяемые как решение краевых задач:
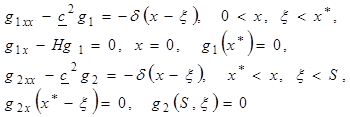 (10)
(10)
В (9)
![]()
![]() (11)
(11)
![]() .
.
С помощью функций Грина (9) и формул Грина [3, 4]:
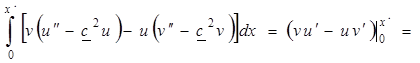
![]() ; (12)
; (12)
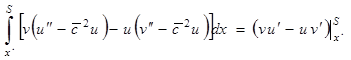
(6)–(8) сводится к решению нелинейного интегрального уравнения типа Гаммерштейна, системе двух нелинейных уравнений относительно ![]() и
и ![]() и квадратуре:
и квадратуре:
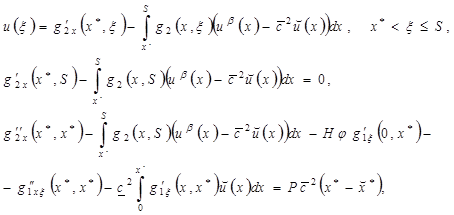 (13)
(13)
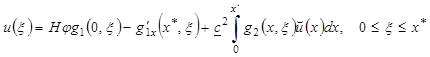 (14)
(14)
Конечномерная аппроксимация уравнений (13), (14) позволяет свести задачу к нелинейной алгебре относительно узловых значений ![]() и чисел
и чисел ![]() и
и ![]() .
.
Так как задача не содержит явно времени ![]() , то с определенной погрешностью в качестве ее приближенного решения можно принять:
, то с определенной погрешностью в качестве ее приближенного решения можно принять:
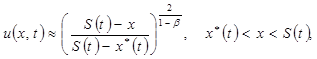 (15)
(15)
где ![]() — решение задачи Коши:
— решение задачи Коши:
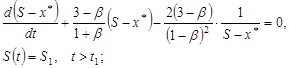 (16)
(16)
Конечномерная аппроксимация квадратуры (14) и замена уравнений (16) разностными в данном случае приводят к системе нелинейных уравнений относительно узловых значений ![]() и чисел
и чисел ![]() и
и ![]() :
:
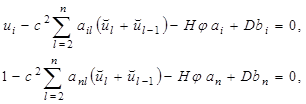 (17)
(17)
![]()
где
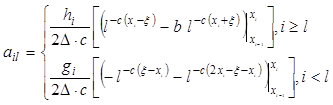
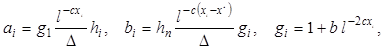
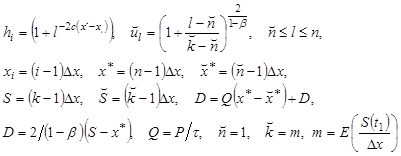 (18)
(18)
Приближенное решение задачи (1)–(2) будем искать в виде соответствующего стационарного решения, считая ![]() и
и ![]() :
:
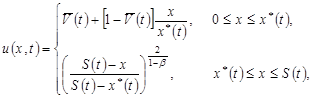 (19)
(19)
![]() .
.
Краевые условия при ![]() выполняются автоматически. Дифференциальные уравнения и краевые условия удовлетворимы в смысле общих тепловых балансов с учетом условия сопряжения [4, 5]:
выполняются автоматически. Дифференциальные уравнения и краевые условия удовлетворимы в смысле общих тепловых балансов с учетом условия сопряжения [4, 5]:
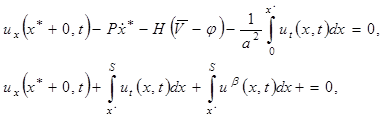 (20)
(20)
Полагая ![]() , после вычисления производных и интегралов для определения
, после вычисления производных и интегралов для определения ![]() и
и ![]() приходим к задаче Коши:
приходим к задаче Коши:
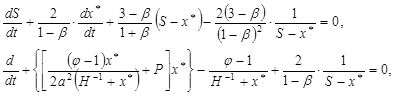 (21)
(21)
Заменяя производные конечными разностями, получаем систему нелинейных уравнений относительно ![]() и
и ![]() на данном временном слое:
на данном временном слое:
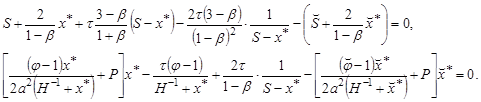
Приведенные алгоритмы получения приближенных решений реализованы на ЭВМ. Результаты численных расчетов сведены в таблицы.
|
|
|||||
|
|
1 |
1 |
2 |
2 |
|
|
|
2 |
3 |
2 |
3 |
|
|
|
1.89 |
2.05 |
1.50 |
1.66 |
|
|
|
3.08 |
3.24 |
2.12 |
2.30 |
|
|
|
|||||
|
|
1 |
1 |
2 |
2 |
|
|
|
2 |
3 |
2 |
3 |
|
|
|
2.48 |
2.64 |
1.91 |
2.08 |
|
|
|
3.71 |
3.87 |
2.33 |
2.72 |
|
Рецензенты:
Шхануков-Лафишев М.Х., д.ф.-м.н., профессор, ФГБУН Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН, г. Нальчик;
Ашабоков Б.А., д.ф.-м.н., профессор Высокогорного Геофизического Институт, г. Нальчик.



