В настоящее время, проблема повышения качества высшего образования выходит на первый план. Это связано со многими обстоятельствами, среди которых отметим реформу Российской системы образования, необходимость развития инновационных отраслей промышленности, переход к новым стандартам обучения и др.
Так, например, главной целевой установкой в реализации современных образовательных стандартов поколения 3+ являются компетенции, полученные учащимися в ходе обучения [3,4]. Заявленный компетентностный подход предусматривает иную роль обучаемого в учебном процессе. Резко возрастает значимость самостоятельного освоения материала, периодического контроля знаний, мотивации к образованию, коммуникационных навыков и т.д. Все эти вопросы нуждаются в углубленном изучении, детальной проработке [2,5].
По сути дела, в системе высшего образования наблюдается явно выраженный парадокс. С одной стороны, сама технология обучения остается традиционной, групповой в силу соображений экономической эффективности, наличия готовых методик, сложившейся управленческой структуры вузов и т.п. С другой стороны, время требует развития индивидуального обучения, самообразования, обширных, в том числе и международных коммуникаций.
В этой связи, интересным представляется ответ на вопрос: «Насколько исчерпан потенциал традиционного обучения учащихся в учебных группах?». Многие преподаватели могут констатировать тот факт, что учебные группы часто различаются между собой по критерию «достигнутый результат», хотя, зачастую, начальный потенциал обучающихся различается незначительно. Очевидно, что это явление определяется рядом показателей, характеризующий группу с точки зрения ее сплоченности, психологической совместимости, направленности на результат, наличия лидеров и т.д.
В связи с этим, весьма актуальной представляется задача промоделировать процесс обучения в группе, с учетом ряда предположений и ограничений, чтобы выявить наиболее общие закономерности и сделать вывод о потенциале группового метода обучения.
В данной статье представлены основания для разработки имитационной модели, реализующей высказанные выше соображения.
Рассматриваемая модель относится к группе микромоделей, описывающих процесс обучения на уровне конкретного индивидуума. Поскольку в этом процессе существенную роль играют индивидуальные характеристики обучающегося, а также превалируют субъективные оценки качества обучения, модель содержит ряд существенных упрощающих предположений, которые формулируются ниже.
Будем считать, что существует некоторая переменная Ji(t) характеризующая текущий уровень знаний i-ого студента в функции времени. Введем также величину Ii(t), представляющую объем информации, предлагаемой для освоения. Понятно, что Ji(t)≤Ii(t) для всех студентов без исключения. Отношение: К=<Ji(t)>/<Ii(t)>, где угловые скобки обозначают усреднение по времени обучения, характеризует эффективность обучения, которую легко перевести в оценку.
Изменение во времени величины Ji(t) в первом приближении можно описать дифференциальным уравнением вида:
(1)
где первое слагаемое справа учитывает «утрату» знаний за счет забывания, перенасыщения информацией и т.д., второе слагаемое – наоборот, приобретение знаний, передаваемых извне (от преподавателя, в процессе самообучения или обучения в группе).
Коэффициент µ определяет порядок «утраты» (забывания) информации и зависит от времени и набора индивидуальных характеристик γi обучающегося. Параметр α определяет степень усвоения информации и эффективность «переработки» ее в знания. Он также зависит как от времени, так и от набора индивидуальных характеристик учащегося.
Введем ряд предположений относительно величин, входящих в уравнение (1). Величину Ii(t) представим в виде:
(2)
где первая составляющая – информация, передаваемая от преподавателя в соответствии с расписанием занятий, второе слагаемое – информация, приобретенная в процессе самостоятельной работы, последнее слагаемое представляет информацию, полученную при общении с другим обучающимся в процессе взаимного обучения в группе.
Учтем также, что:
(3)
Иначе говоря, ученик в процессе самостоятельной работы не может получить информацию больше той, что предназначена для усвоения. А в процессе общения с другим учащимся он может, максимум, получить информацию, равную разности текущих уровней знаний того и другого.
Заметим также, что в первом приближении мы не вводим зависимости Ip от индекса i, то есть, все учащиеся получают одинаковый объем информации от преподавателя (нет индивидуального обучения).
Относительно функций µi(t,γi) и αi(t,γi) могут быть выдвинуты различные предположения. Простейший вид таких функций – линейные функции вида:
где введены обозначения: tact - время активной работы, представляющее собой сумму времени работы преподавателя, времени самостоятельной работы и времени обучения в группе, δi- параметр накопления интеллектуальной усталости (вообще говоря, зависящий от индивидуальных характеристик личности учащегося).
Смысл этих выражений понятен: с увеличением времени активной интеллектуальной деятельности за счет возрастающей утомляемости коэффициент утраты информации возрастает, а коэффициент усвоения – убывает. При этом мы считает, что параметр усталости δ в том и другом выражении одинаковый (хотя это и не обязательно так, но в первом приближении такое предположение представляется оправданным).
Что касается значений µi0, αi0 и δi, то их, опять же, в первом приближении можно считать не зависящими от времени и полагать, что они полностью определяются набором индивидуальных характеристик учащегося, например, регрессионными уравнениями вида:
где wi – коэффициенты регрессии. Точно такими же соотношениями определяются коэффициенты αi0 (и, возможно, δi), только коэффициенты регрессии, конечно, будут другими.
Индивидуальные параметры учащегося γi – это достаточно известные в теории обучения характеристики: уровень интеллекта, мотивация, внимательность, концентрация на задаче и т.п. Их следует перед моделированием для конкретного контингента учащихся определять по результатам соответствующих тестов. Заметим, что если это сделать затруднительно, то можно в процессе моделирования их разыграть в соответствии с нормальным распределением, в котором в качестве параметров (медианы и среднеквадратичного отклонения) использовать некоторые средние данные по контингенту обучения, полученные, например, по результатам вступительных экзаменов (или результатам ЕГЭ). Это достаточно корректно, поскольку хорошо известно, что распределение большинства индивидуальных способностей хорошо описывается именно таким распределением Гаусса.
По результатам тестов уже прошедших обучение групп (или из других источников) следует также определить и коэффициенты регрессионных уравнений, описывающих влияние этих индивидуальных характеристик на базовые параметры µi0, αi0 и δi.
Перед тем, как описать конкретную организацию процесса моделирования, сделаем несколько существенных замечаний.
Первое замечание касается выбора единицы измерения времени, поскольку этот выбор зависит от задачи моделирования. Если стоит задача рассмотреть процесс усвоения информации в течение семестра (части семестра), то удобно в качестве такой единицы избрать академический час (45 минут), а все моделирование проводить в течение недели (или двух, если в институте принято двухнедельное расписание). В этом случае можно базовые параметры µi0, αi0 и δi смело считать постоянными и, более того, постоянным можно считать и функцию I(t).
Если же стоит задача рассмотреть весь процесс обучения за все время обучения (4 года или более), то в качестве единицы времени следует выбрать учебную неделю (а, возможно, и семестр). Очевидно, что в этом случае, как базовые параметры, так и функцию I(t) уже нельзя считать постоянными величинами.
Положим I(t)= const, а также посчитаем постоянными все базовые параметры µi0, αi0 и δi. В этом случае уравнение (1) легко интегрируется:
При t<<1/µ 
, то есть, знания накапливаются пропорционально времени обучения (при условии αI>J0µ), что вполне логично: «забывание» мало и сообщается информация, превышающая первоначальный уровень знаний.
При t>>1/µ 
, что тоже логично: при очень больших временах обучения первоначальный уровень знаний J0 уже не имеет значения и достигнутый уровень зависит от баланса параметров усвоения и утраты информации. Заметим, что из очевидного J(t)/I(t)≤1 следует ограничения на усредненные значения: <α>≤<µ>. Это, впрочем, не означает, что локально, в определенные моменты времени α(t) не может быть больше µ(t).
Итак, в целом, весь процесс обучения можно описать следующим образом. Преподаватель дает определенную информацию за единицу времени всем учащимся в одинаковом объеме, но усваивается она по-разному, в соответствии с конкретным значением коэффициента αi, зависящим от индивидуальных особенностей и прилагаемых усилий данного учащегося. Учащиеся, у которых этот коэффициент мал (или велик коэффициент утраты информации), могут увеличить свой уровень освоения информации либо за счет дополнительных самостоятельных занятий, либо получая дополнительные знания от учащихся, имеющих более высокий по сравнению с ними уровень знаний. К каким именно товарищам по группе обратится данный учащийся, зависит от, условно говоря, «коэффициента симпатии», который также нуждается в определении по результатам тестов на совместимость. Для идентификации подобных коэффициентов существуют свои методики, например, методы соционики [1].
Предполагается, что периодически учащиеся каким-то образом оценивают свой уровень освоения информации (либо сами, либо с помощью текущего контроля, организованного преподавателем). Если он достаточен (по мнению учащегося, а это мнение, вообще говоря, может отличаться от мнения преподавателя), учащийся прекращает занятия и переходит в состояние отдыха, в котором информации может только утрачиваться. Если уровень освоения недостаточен, то учащийся выбирает, заниматься ли самостоятельно или обратиться за помощью.
При моделировании принципиальным является деление всего времени на активное и время отдыха: в активное время производится усвоение новых знаний, правда, с частичной утратой, так как забывание происходит непрерывно. Во время же отдыха знания могут только утрачиваться. В активной фазе время работы с преподавателем определяется учебным планом и расписанием, а время самостоятельной работы и работы с партнером по обучению должно вычисляться.
В первом приближении для такого вычисления можно использовать следующие простые соотношения:
Здесь введением коэффициентов А и В учтено, что эффективность самообучения и обучения в группе отличается от обучения с преподавателем. Ряд проведенных наблюдений дает для А значение на уровне 2-3, то есть, самообучение требует для освоения того же материала в два-три раза больше времени, чем при непосредственном обучении преподавателя. Что касается коэффициента В, то авторами, на основании проведенных экспериментов, сделано предположение, что он того же порядка.
Таким образом, представленный алгоритм может быть реализован в виде многоагентной модели в среде имитационного моделирования (GPSS, Arena, AnyLogic и др.) с целью получения конкретных количественных и качественных характеристик, позволяющих оценить потенциал учебной группы с точки зрения эффективного достижения целей образования.
На рис.1. приведена блок-схема процесса моделирования.
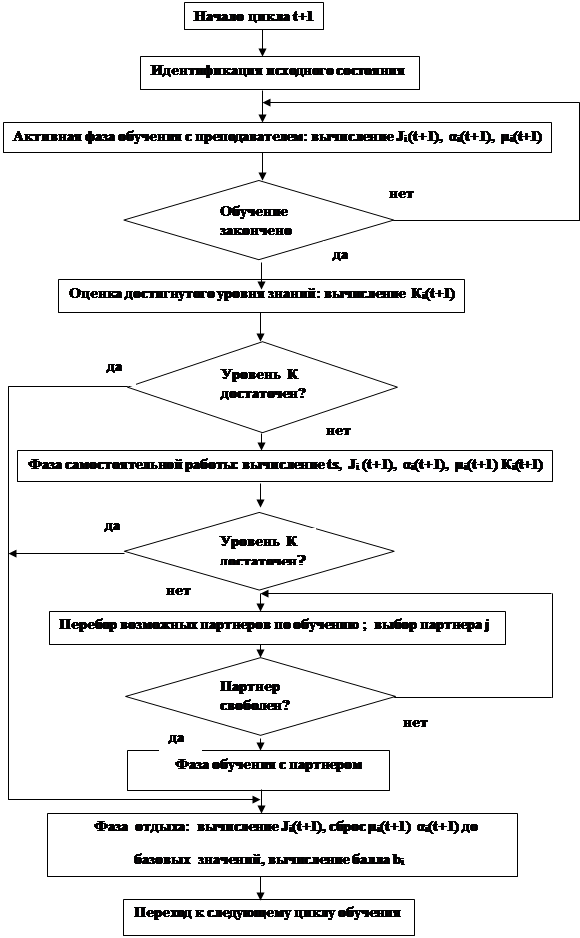
Рисунок 1 – Блок – схема процесса моделирования
Рецензенты:
Хаймович И.Н., д.т.н., профессор кафедры информационных систем и компьютерных технологий ЧОУ ВО «Международный институт рынка», г. Самара;
Прохоров С.А., д.т.н., профессор, зав. кафедрой информационных систем и технологий ФГБОУ ВПО Самарского аэрокосмического им. академика С.П. Королева – Национального исследовательского университета, г. Самара.