Все эти переходные процессы для различных регионов обладали особенностями, однако, в первой половине XX века стала очевидной тенденция, претендующая на общность. Динамика современного мирового экономического развития такова, что рабочая сила перемещается из сфер материального производства в сферу услуг: происходит переквалификация рабочих мест. Все большее количество отраслей материального производства становятся все более услугооказывающими, повышение наукоемкости продукции ведет к росту стоимости услуг в цене товара. Эта тенденция порождает следующие вопросы:
§ каковы причины такого перераспределения трудовых ресурсов,
§ что ожидает мировую экономику в будущем,
§ каков прогноз социальной структуры будущего.
В настоящее время известны следующие модели занятости в экономике [5]: двухсекторная модель, трехсекторная модель Фишера (1935) и Кларка (1940), пятисекторная модель Белла (1973), четырехсекторная модель Пората (1977), шестисекторная модель Зингельманна (1978), двухполюсная модель общественного производства.
Анализ многосекторных моделей, применительно к Японии, был выполнен в работе [5], применительно к США – отражен в публикациях [3] и [2]. В настоящей работе, на примере экономики США, эволюция структуры общественного производства представляется, как результат межсекторальной конкуренции.
Распределение рабочей силы по трём секторам экономики США (сельское хозяйство, производство, сфера услуг) в миллионах человек на интервале времени с 1790 года по 2000 год отражено на Рис. 1 [3].
Из наблюдений следует, что численности занятых в сельском
хозяйстве и в производстве ведут себя экстремально. Максимум занятости в
сельском хозяйстве был достигнут примерно в 1900 году (
миллиона человек), максимум занятости в
производстве достигнут примерно в 1970 году (
миллиона
человек). При этом наблюдается интенсивный рост числа занятых в сфере услуг.
Наблюдения означают следующее: немногочисленные вначале представители рабочей силы, занятые в сфере производства и в сфере услуг, постепенно вытесняют представителей сельского хозяйства, а в дальнейшем и трудящиеся в производстве вытесняются сферой услуг. Такое перераспределение рабочей силы можно интерпретировать как результат конкуренции между секторами экономики за трудовые ресурсы.
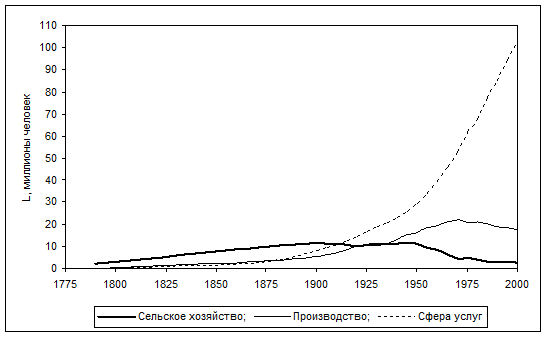
Рис. 1. Распределение рабочей силы по трём секторам экономики США в миллионах человек на интервале времени с 1790 года по 2000 год [3]
Подобный тип конкуренции может быть формализован посредством обобщения модели логистического роста Ферхюльста (1):
,
(1)
,
где
– численность занятых в 
-ом секторе экономики, выраженная в
миллионах человек,
– удельная скорость роста числа занятых в
-ом секторе экономики,
– ёмкость экономики по отношению к
численности занятых в -ом секторе, выраженная
в миллионах человек.
Уточним
смысл ёмкости . Для сельскохозяйственного
сектора экономики 
миллиона человек, при
этом общая численность занятых в экономике составила 
миллиона человек. Таким образом, 
– это общая численность занятых в
экономике, при которой в сельском хозяйстве достигается максимум числа занятых,
и эта численность занятых достигается в 1900 году. Для производственного
сектора 
миллиона человек, и эта
численность связана с 1970 годом, то есть с тем моментом времени, когда 
миллиона человек.
Отметим,
что величины 
, 
и
соответствующие им времена определены визуально: «сняты» с графика (Рис. 1).
Для их уточнения следует выполнить численный анализ модели (1).Величину 
можно было бы определить, если бы была
известна долгосрочная динамика общей занятости 
.
Пусть, например, подчинена уравнению
(2) [3]:
,
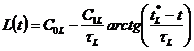(2)
где 
– общая занятость, измеряемая в
миллионах человек, 
– время,
соответствующее максимальной скорости роста ,
измеряемое в годах, 
– время,
ограничивающее скорость роста , измеряемое
в годах,
, 
,
, 
.
Тогда
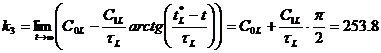. (3)
В этом случае сценарий эволюции структуры общественного производства (в границах трехсекторной модели) становится вполне определенным.
Результаты численного интегрирования уравнений (1) отражены в Таблице 1 и на Рис. 2.
Таблица 1
Результаты численного интегрирования уравнений (1).
|
|
|
|
|
0.0212 |
0.0361 |
0.0446 |
|
|
|
|
|
31.25 |
87.53 |
253.8 |
|
|
|
|
Величине 
соответствует
. Величине 
соответствует
. Самая высокая ёмкость экономики США
принадлежит сфере услуг: 
и теоретически
может быть достигнута за бесконечное время. Однако уже к 2085 году численность
занятых в сельском хозяйстве не превысит порядка единицы (приблизится к нулю),
а к 2245 году исчезнет занятость и в производстве (Рис. 2). Таким образом, уже
в 2245 году всё экономически активное население США будет занято в сфере
обслуживания.
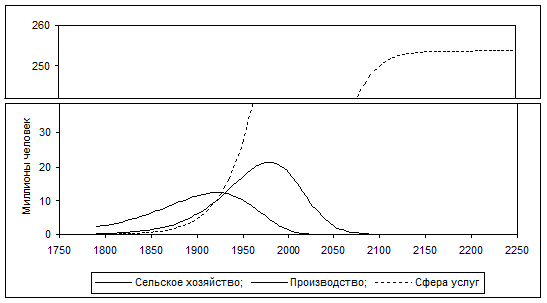
Рис. 2. Концентрация рабочей силы в секторах экономики США
Обратим внимание на следующий факт. Удельные скорости роста находятся в следующих отношениях: 
. В таких же отношениях находятся и
ёмкости :
.
Оба эти условия в нашем случае увеличивают конкурентоспособность 
-го сектора по отношению к -му сектору экономики. Однако удельные
скорости роста не являются определяющими
в процессе конкурентных отношений, соответствующих модели (1).Решающим
фактором, определяющим направление развития процесса, являются ёмкости (биологи называют такую ситуацию 
-отбором [4]).Тот сектор экономки,
который имеет потенциально большую ёмкость, вытесняет конкурента, независимо от
удельных скоростей роста. В нашем случае оба фактора оказались «на стороне»
сферы услуг.
Возможен ли подобный сценарий развития экономики? Теоретически – да, если выполняются два условия:
1. Модели, положенные в основу наших рассуждений верны (в частности, уравнения (1) адекватны исследуемому процессу, и справедливо уравнение общей занятости (2), которое, в сою очередь, должно быть подчинено динамике численности населения).
2. Положение равновесия, соответствующее сценарию – устойчиво.
Первое условие предполагает адекватное описание динамики общей численности населения, обеспечивающее выполнение долгосрочного прогноза. Напомним, что формализация динамики численности населения в работах[3], [2] была проведена на ограниченном интервале времени. Экстраполирование названной динамики приводит к постепенной стабилизации численности населения. Уместно отметить, что еще в первой половине XX века демографы заметили, что население стран Западной Европы уже имело тенденцию к снижению, а современная динамика численности населения Японии, например, демонстрирует спад. Для долгосрочного прогнозирования численности населения необходимо моделировать общий прирост численности, который зависит от функций рождаемости и смертности, брачности и разводимости, мобильности населения. Подобная задача демографического анализа выходит за рамки настоящего исследования.
Основное внимание уделим проверке выполнимости второго условия: исследуем на устойчивость интересующее нас положение равновесия системы уравнений (1).
Качественный анализ уравнений (1). Систему (1) для удобства запишем в следующем виде:
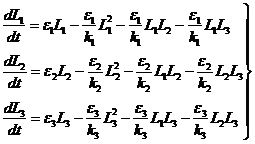(4)
В системе (4) теоретически возможно множество положений равновесия:
, 
,
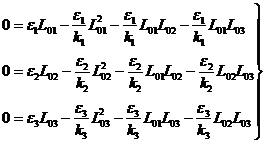(5)
Нас интересует сценарий, отражённый на Рис. 2, то есть положение равновесия, при котором:
, 
(6)
Нелинейные функции, стоящие в правых частях (4) разложим в
ряд Тейлора с точностью до слагаемых первого порядка и запишем с учётом
отклонений 
от положения равновесия:
, 
,
Линеаризованные функции примут вид:
, 
,
,
,
, 
Система в отклонениях:
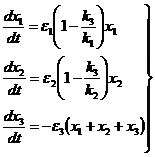(7)
Используя вид решения
,
переходим от системы (7) к однородной системе линейных алгебраических уравнений:
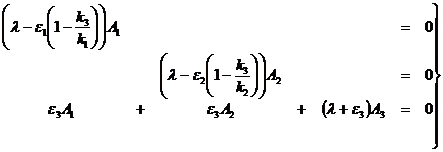(8)
Характеристические
числа 
определим из условия:
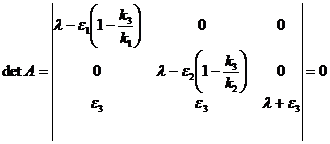(7)
Раскрывая определитель (7), а также используя полученные
ранее величины коэффициентов и , находим:
,
,
Поскольку все 
, то положение
равновесия (5) – асимптотически устойчиво.
Вывод, который следует из качественного анализа модели (1), позволяет полагать теоретическую возможность сценария развития экономики, который отражён на Рис. 2.
Заключение. Ранее было отмечено, что в системе (1) теоретически возможно множество положений равновесия, однако модель не предусматривает механизма перехода от одного положения равновесия к другому. Не рассматриваются факторы, которые могут привести к подобным изменениям. Таким образом, долгосрочный прогноз распределения занятости по секторам экономики (на основании рассмотренной модели) выполнять не следует. Тем не менее, результаты моделирования не противоречат данным официальной статистики современности. В США сфера услуг является важнейшим источником роста ВВП и главным объектом для трудоустройства населения, и, в соответствии с модельным представлением, будет являться таковой хотя бы в ближайшей перспективе.
Рецензенты:Соболев В.Ю., д.э.н., профессор, зав. кафедрой «Экономики предпринимательской деятельности» ИЭП ННГУ им. Н.И. Лобачевского, г.Нижний Новгород;
Чкалова О.В., д.э.н., профессор, зав. кафедрой «Торгового дела» ИЭП ННГУ им. Н.И. Лобачевского, г.Нижний Новгород.