Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Обеспечение надежной и безопасной транспортировки «аномальных» нефтей являет­ся сложной технической и технологической задачей. Все многообразие процессов, воз­никающих при транспортировке «аномальных» нефтей еще недостаточно изучено.

Точное определение реологических характеристик структурированных дисперсных систем, к которым относятся высоковязкие и высокопарафинистые нефти, необходимо для выявления общих закономерностей их образования, разрушения, устойчивости. Наи­более полную информацию о реологических свойствах подобных систем несет кривая течения, т.е. зависимость напряжения сдвига от скорости сдвига при сдвиговой дефор­мации.

Как известно, все неньютоновские жидко­сти отличаются от классической ньютоновской жидкости видом зависимости скорости сдвига от величины касательного напряжения.

Иногда кривые течения жидкостей могут иметь более сложный нетрадиционный вид. Общую характеристику течения неньютоновских жидкостей составили Г.В. Виноградов и В.П. Павлов. Они же сформули­ровали понятие сверханомалии вязкости как явления снижения сопротивления сдвигу в условиях перехода между установившимися режимами деформирования – от течения дисперсной системы практически без разрушения коагулятивной структуры к другому режиму – с интенсивным необратимым разрушением структурного каркаса [1].

В данной работе проводились исследования смеси нефтей Усинского и Ярегского ме­сторождений в большом диапазоне температур и при различном их соотношении (от 5 до 30% ярегской нефти), а также высокопарафинистой нефти Харьягинского месторожде­ния.

В ходе экспериментов установлено, что данные нефти и смеси нефтей имеют тиксотропные свойства. Степень разрушения структурной решетки в аномальной нефти зависит от скорости сдвига (скорости перекачки) и от времени воздействия нагрузки. При остановке перекачки структура высокопарафинистой нефти начинает восстанавли­ваться. Способность вещества с течением времени восстанавливать разрушенную струк­туру называется тиксотропией. Восстановление структуры для каждой нефти происходит через разное время. Полное восстановление разрушенной структуры происходит через значительный промежуток времени [3].

При определенных температурах и определенных концентрациях нефтей выявлено явление сверханомалии вязкости.

Одним из методов подготовки таких нефтей к транспорту является путевой подогрев. Именно данный метод и будет рассматриваться далее, как наиболее просто реализуемый в рамках существующей трубопроводной системы обозначенных месторождений.

Анализ работы трубопровода, оснащенного системой электроподогрева, и вывод критериальных уравнений должны базироваться на мощной теоретической базе. Моделирование гидродинамических и тепловых процессов может помочь в установлении взаимодействия между теоретической базой и «полевым» экспериментом.

Внутритрубное неизотермическое течении нефти представляет собой сложную систему, коэффициент теплоотдачи которой зависит от множества параметров:

α = ƒ( tн.ср, tc, cp,dн,dвн, λн, υн, ρн), (1)

гдеtн.ср– начальная средняя температура,С

λн - коэффициент теплопроводности нефти, Вт/(м·К);

dн– средняя вязкость нефтепродукта, сСт

υн- средняя скорость потока нефти, м/с;

ρн - средняя плотность нефти, кг/м3 .

При проведении экспериментов, полученные данные зависимостей зачастую носят частный характер, их справедливость может быть обусловлена только в тех условиях, при которых проводился данный опыт. Чтобы выйти из сложившейся ситуации, применяется теория подобия, которая позволяет эти частные результаты обобщить с целью расчета коэффициента теплообмена[1].

Критериальное уравнение, характеризующее теплообмен при внутритрубном течении нефти с учетом эффекта подогрева пристеночного слоя потока могут быть записаны следующим образом:

(2)

где A,B,C1- коэффициенты

Также, при использовании анализа размерностей и теорию подобия, было получено уравнение, с помощью которого можно найти значение температуры стенки в зависимости от мощности системы электроподогрева, используемой при нагреве нефти, и средней температуры стенки трубы по поперечному сечению:

(3)

где С2, D - коэффициенты,

Используемый параметр РK - безразмерный параметр, определяемый как:

, (4)

где Сз–коэффициент,

PL - линейная мощность системы электроподогрева, идущая на нагрев нефти, Вт/м.

Для получения функциональной зависимости Nuж и tc/tн.ср было решено использовать комбинационные квадраты для ламинарного и турбулентного режимов течения нефти во время эксперимента [5].

Поставленный эксперимент был выполнен в программном комплексе ANSYS 14.0, в котором была создана компьютерная математическая модель трубопровода. Рассматриваемые варьируемые величины находились в следующих пределах:

- для ламинарного режима течения: 400 <Reж< 2000; 882 <Ргж< 20588 и 20 < РL< 350;

- для турбулентного режима течения: 2850 <Reж< 10000; 588 <Ргж< 5588; 20 <РL< 350

Критерий Нуссельта Nuж при средней температуре нефти определялся по формуле:

(5)

где Q — тепловая мощность, переданная жидкости, Вт.

– внутренний диаметр трубопровода, м.

F – площадь внутренней поверхности стенки трубы, м2.

Во время проведения моделированного процесса значения tc и tн ср регистрировались для ламинарного и турбулентного режимов течения, после чего устанавливались значения Nuжи заносились в таблицу. В Табл. 3 представлены результаты.

Значения коэффициентов А, В и С1были определены следующим образом.

Приведем уравнение (2) к виду:

lgNuж = lgC1 + AlgReж + BlgPrж (6)

Таблица 1

Комбинационный квадрат проведения экспериментов при ламинарном режиме течения нефти

Таблица 2

Комбинационный квадрат проведения экспериментов при турбулентном режиме течения нефти

Таблица 3

Результаты экспериментов

Была построена зависимость числа Нуссельта Nuж от числа Рейнольдса Reж в логарифмических координатах. При графическом отображении критериальной зависимости на графике отображается семейство линейных зависимостей.

При критерии Rеж коэффициент А определяется по анализу графика зависимостей (прямых линий) и является тангенсом угла наклона прямой линии к оси абсцисс [2].

Для ламинарного потока A = 0,521; для турбулентного потока A = 0,863. Дальнейший расчет (6) сводиться к виду:

(7)

При критерии Ргж коэффициент В определяется по анализу графика зависимостей (прямых линий) и является тангенсом угла наклона прямой линии к оси абсцисс. Для ламинарного потока В = 0,252; для турбулентного потока В = 0,258.

Постоянную С1 найдем из уравнения (2), приведя его к виду

(8)

Тогда для ламинарного потока С1 = 0,283; для турбулентного потока С1 = 0,026.

В конечном итоге, были найдены неизвестные коэффициенты, что позволило получить критериальные уравнения следующего вида:

- для ламинарного потока

(9)

- для турбулентного потока

(10)

Среднеквадратичная погрешность расчета составила 1,9% по формуле (9) и 0,9% по формуле (10)

Приведенный метод не подходит для определения функциональной зависимости tc/tH,cp, так как tc/tH,cp,=ƒ(РK) описывается уравнением не степенного вида. Для получения зависимости tc/tH,cp = ƒ(Rеж, Рк) использовался метод получения эмпирических формул, предложенный В.М. Мордашевым [6].

Для нахождения средних геометрических значений tc/tн,cp значения tc/tн,cp сначала были прологарифмированы, а далее найдены средние значения логарифмов при одинаковых значениях Rеж и Рк, Полученные данные представлены на (Рис. 1, 2).

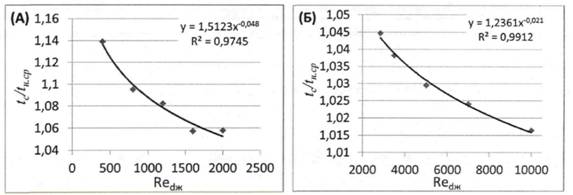
Рис. 1. Зависимость средних геометрических значений tc/tH,cpот Rеж для: ламинарного режима(А), турбулентного режима (Б)

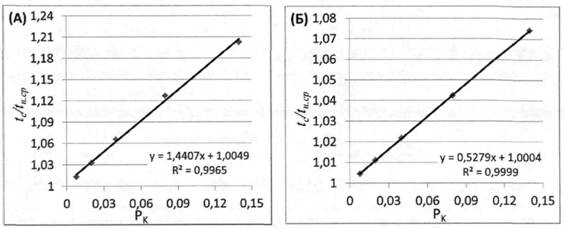
Рис. 2 Зависимости средних геометрических значений tc/tн,cpот Ркдля: ламинарного режима (А), турбулентного режима (Б)

Полученные зависимости были аппроксимированы степенными и линейными уравнениями:

- для ламинарного потока

(11)

(12)

- для турбулентного потока

(13)

(14)

После преобразований выявлены следующие зависимости для ламинарного и турбулентного потока:

- для ламинарного потока

(15)

- для турбулентного потока

(16)

Среднеквадратичная погрешность расчета, произведенная по формуле (15), составляет 2,5 % и по формуле (16) – составляет 0,9%. Исходя их перечисленного можно подвести, что были найдены все неизвестные коэффициенты в искомых уравнениях (2) и (3).

Необходимо уточнить, что в уравнениях (9) и (10) числа Прандтляи Рейнольдса ( расчет производится при средних температурах нефти, которые вычисляются по длине участка трубопровода. А уравнения (15) и (16) справедливы при средних температурах стенки трубы и потока нефти в поперечном сечении определенной точки трубопровода [4].

Построенная модель трубопровода, оснащенная системой электроподогрева в программном комплексе ANSYS 14.0, может быть использована при дальнейших расчетах на предприятиях для установления зависимостей теплообмена потока жидкости с окружающей средой и стенкой.

Рецензенты:

Земенков Ю.Д., д.т.н., заведующий кафедрой «Транспорт углеводородных ресурсов» ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень;

Торопов С.Ю., д.т.н., профессор, ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень.