До последней четверти XX века вопрос «зачем изучать математику» был бы встречен с недоумением. Непререкаемый авторитет математике обеспечивал её вычислительный аппарат. С массовым распространением компьютеров и информационных технологий умение правильно вычислять перестало быть безусловным приоритетом даже для инженера. Сейчас даже профессиональные математики нередко проводят выкладки с помощью пакетов символьных вычислений: Mathematica, Maxima, Mapple, MathCAD и др. В итоге в обществе возникает ощущение, что можно отказаться от систематического изучения математики: «все равно все вычисляется в такой-то программе». Причина этого заблуждения сформулирована в виде известной шутки: «Нематематики считают, что математики считают».
Проблемы, связанные с анализом того, что есть математика, ее места и роли, были предметом размышления крупнейших математиков [1-3]. Таким образом, несомненна необходимость перманентного переосмысления места и роли математики в современной науке, технике, экономике, искусстве и в конечном итоге в образовании [4; 5]. В обществе может возобладать точка зрения о якобы «ненужности» и «бесполезности» математики в современном мире, что приведет к катастрофе не только технологической, но и мировоззренческой. Следует понять, что такое математика вообще, что такое математика в современном мире и «зачем её изучать следует» даже в информационном обществе. В этом и состоит цель нашего исследования. Цель определяет задачи исследования: формализовать представление о том, что такое математика в «цифровую эпоху», выделить актуальные аспекты сложного многогранного понятия «математика», на основании этого определить основные приоритеты математического образования в информационном обществе.
Карл Гаусс в своё время назвал математику царицей всех наук, отдавая ей особое место в сфере человеческого знания. Математика служит для других наук языком и методом изучения. Являясь, пожалуй, самой строгой из всех наук, она не имеет собственного строгого и общепринятого определения. На протяжении всей своей истории математика преобразовывалась сама, преобразовывалось и понятие о математике. Представление о математике сегодня выражено не её «определением», а набором афоризмов: «Математика - это язык, на котором написана книга природы» (Г. Галилей), «Математика – это строгий язык, служащий для перехода от одних опытных суждений к другим» (Н. Бор), «Математика – это иерархия формальных структур» (Н. Бурбаки). Это лишь малая часть суждений, показывающая разнородность представлений о математике. Помимо вопроса определения математики, интересными и дискуссионными являются вопросы о её природе (основаниях), её методологии, целях и связи с реальным миром. Ответы на них также неоднозначны и значительно изменялись со временем, создавая различные философские течения.
Мы согласны, что сформулировать ёмкое общепринятое определение математики не удалось. Статья «Математика» из «Большой советской энциклопедии» «Математика – это наука о количественных отношениях и пространственных формах действительного мира» (А.Н. Колмогоров) основана на трактовке математики, предложенной ещё Ф. Энгельсом. Данное определение в целом отражало состояние, роль и место математики на тот момент. Но сегодня это определение математики трудно признать исчерпывающим. Например, в математике большую роль играет актуальная бесконечность, хотя в реальном мире нет «бесконечных количеств», все рассматриваемые объекты конечны, утверждение об их потенциальной бесконечности как минимум небесспорно. Нам неизвестны реальные объекты, состоящие даже из счетного числа элементов, не говоря о кардиналах большей мощности. Неевклидова геометрия «обязана» своим рождением специфике пятого постулата Евклида, который, в отличие от других постулатов, проверить экспериментально в конечной области невозможно (при традиционной интерпретации понятия «прямая»). Нет прямых прототипов для бесконечно малых, рассматриваемых в «нестандартном анализе» [6].
Для столь многогранного понятия, как «математика», нельзя сформулировать бесспорное «работоспособное» определение. Мы предложили [7] применить не дедуктивный, а индуктивный способ описания объёма понятия «математика». Применим метод моделирования: рассмотрим систему моделей математики с позиций математического образования. С этой позиции ответ на вопрос чему и как учить зависит от того, кого учить! Отсутствие явного учета особенностей обучаемого обычно отмечают в качестве недостатка классической трактовки методической системы в смысле А.М. Пышкало [8]. Обучение математике является неотъемлемой частью системы профессиональной подготовки студента – будущего специалиста в области экономики [9; 10] и инженерии [11; 12]. Этот процесс рассмотрим на двух уровнях: 1) на содержательном; 2) на операционально-деятельностном. На содержательном уровне нужно отобрать такой математический контент, соответствующий выбранной студентами профессии. На операционально-деятельностном уровне следует организовать формирование навыков интеллектуальной деятельности, обучение обобщенным приемам мышления.
В силу вышесказанного наиболее актуальными, на наш взгляд, являются следующие представления о математике. Математику можно рассматривать, во-первых, как область деятельности (рис. 1); во-вторых, как аппарат обработки информации (рис. 2).
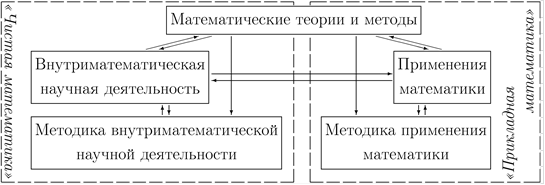
Рис. 1. Модель математики как области деятельности
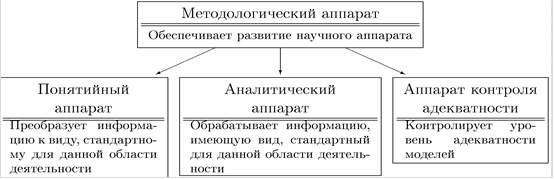
Рис. 2. Аппаратная модель математики - математика как аппарат обработки информации: формализации, перевода, преобразования, контроля
Рассмотрим содержание курса математики для экономистов и инженеров с позиций этих моделей.
I. Исходя из деятельностной модели математики содержание учебного курса должно включать в себя:
1) представление о стратегиях математической и общенаучной деятельности и распространение этих стратегий на другие виды деятельности (формализация информации как этап моделирования, стратегия поиска доказательства, метод восходящего и нисходящего анализа, комбинированного анализа);
2) формирование многопланового, комплексного представления о математических феноменах [13] и связанные с этим дидактико-воспитательные аспекты обучения: эстетический, морально-нравственный и др.;
3) представление о специфике «чистой» и «прикладной» математики, которые во многом различаются методологически, имеют разные системы приоритетов и др., что отражается на восприятии информации «чистым» и «прикладным» математиками, что инженеру и экономисту следует учитывать при привлечении математиков к решению профессиональных задач;
4) формирование понимания связи между профессиональной деятельностью конкретного субъекта и математикой («вопиющий» пример, когда специалист не способен прочесть вслух многозначное число);
5) отражение различных подходов к представлению материала: генетический, формально-логический, «от частного к общему», «от общего к частному» и др. Отметим, что применение генетического подхода, например, к изучению математического анализа «в чистом виде» нецелесообразно, в частности, потому, что первоначальный вариант математического анализа, разработанный Ньютоном, был впоследствии замещен подходом Коши. Разумнее «имитировать» генетический подход, поскольку базовые понятия математического анализа дают большие возможности для демонстрации применения стратегии формализации информации;
6) обучение как формализации информации, так и умению разбираться с формализованной информацией. В данном случае ценно как изложение, ориентированное на получение определения, формулы, описания алгоритма и других математических феноменов, так и представление готового феномена с последующим разбором его содержания.
II. Исходя из аппаратной модели (рис. 2) содержание курса математики должно включать в себя:
1) связь между этапами математической деятельности и математическим аппаратом, используемым на каждом её этапе: формализация, анализ, контроль, интерпретация;
2) формирование целостного представления о математическом аппарате за счет, в частности, позиционирования изучаемого фрагмента математического аппарата в рамках модели на рис. 2. Например, метод Гаусса решения системы линейных уравнений и метод математической индукции, хотя и имеют в названии общий термин «метод», относятся к аналитическому аппарату и, соответственно, к методологическому аппарату математики. На этом основании выделяются ситуации, когда внимание к «деталям», «мелочам» могут оказаться существенными (например, имеет ли функция f(x)=1/x первообразную на интервале, включающем x=0);
3) понимание разделения математических феноменов на категории: понятия, теоремы (формализация отношений), методы;
4) формирование представления об алгебраическом подходе к построению модели [14]. Он представляет собой систему из трех компонентов: а) системы базовых моделей; б) системы типовых преобразований и типовых комбинаций моделей; в) механизма аппроксимирования, предназначенного для (вообще говоря, приближенного) представления объекта в виде результата применения типовых преобразований и типовых комбинаций базовых моделей. Например, применительно к функциям действительной переменной можно отметить, что первые два компонента алгебраического подхода изучаются еще в школе: основные элементарные функции (степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические) и типовые комбинации (сумма, произведение и т.д.). А вот механизм аппроксимирования в средней школе не рассматривается совсем. Это можно использовать для мотивирования студентов к изучению математического анализа, поскольку математический анализ позволил получить набор механизмов аппроксимирования: формула Тейлора, ряд Тейлора, ряды Фурье, сплайны, метод наименьших квадратов и др.;
5) формирование представления о возможности принципиально разных результатов деятельности (и разных оценок этих результатов) в случае существенного различия системы приоритетов, инструментария, методологии к одной и той же ситуации. Например, интерполяционный многочлен Лагранжа по сравнению с представлением функции в виде частичной суммы ряда Фурье обеспечивает точное совпадение значений аппроксимирующего многочлена со значениями исходной функции для заданного множества точек, но значения исходной функции между этими точками могут существенно отличаться от значений аппроксимирующего многочлена Лагранжа. При этом с ростом числа точек ситуация может ухудшаться. В случае аппроксимации частичной суммой ряда Фурье различие в отдельных точках тоже может быть большим, но «интегрально» (в смысле нормы L2[a;b]) с ростом числа слагаемых аппроксимация улучшается;
6) демонстрация обогащения понятийного аппарата других наук с помощью математического аппарата. Например, идея исследований «асимптотического поведения» функций привели в экономике к оперированию с трендами и др. Конечность тренда не должна вводить в заблуждение, поскольку прототипа актуальной бесконечности в реальной жизни нет, а потенциальная бесконечность на практике тоже сталкивается с ограниченностью рассматриваемых объектов (как при увеличении, так и при уменьшении масштаба, например при измельчении масштаба мы постепенно выходим за рамки применимости физической модели, как это происходит в классической и квантовой механике). Таким образом, с одной стороны, математический аппарат (в частности, понятийный) нередко успешно интегрируется физикой, экономикой и др. С другой стороны, идеи, возникающие при применении математики к решению задач экономики, физики, техники, приводят к обогащению понятийного, аналитического и даже методологического аппаратов математики. Например, линейное программирование, созданное для решения задач оптимизации в экономике, привело к появлению таких понятий, как симплекс, целевая функция, базисное решение, двойственная задача и др.
Выводы и апробация. Приоритеты обучения математике основаны на понимании того, что такое математика и какова её роль в информационном обществе. Для профессионального математика естественно было бы сослаться на определение математики, но многочисленные попытки получить безупречную дедуктивную формулировку, на наш взгляд, не завершились однозначным успехом в силу многогранности, многоаспектности математики. Мы предложили использовать индуктивный подход к формированию объёма понятия «математика» с помощью освещения разных аспектов математики, формализованных в виде разных моделей математики. Для экономистов и инженеров наиболее актуальными являются предложенные нами аппаратная модель математики и модель математики как области деятельности. Их анализ позволил выделить ряд приоритетных направлений обучения математике и сделать вывод об актуальности её изучения в информационном обществе и недопустимости катастрофического обеднения культуры при возможном исчезновении её математического компонента. Рассмотрение математики как системы моделей открывает путь к адекватному определению приоритетов современного математического образования будущих экономистов и инженеров:
1) формирование у них многопланового представления о математических феноменах, обучение разделению математических феноменов на категории: понятия, теоремы, методы;
2) формирование понимания связи между профессиональной деятельностью индивида и математикой, демонстрация обогащения понятийного аппарата других наук с помощью математического аппарата;
3) обучение методам формализации, анализа, контроля, интерпретации, развитие умения формализовывать информацию и работать с ней.
В соответствии с этими приоритетами надо изменить содержание математического образования. Для этого следует решить ряд вопросов: а) проанализировать и пересмотреть существующие математические курсы в контексте ИКТ; б) создать систему эталонных моделей для оценки качества математических курсов в условиях применения ИКТ. Эта система предложена нами в [15] и исходит из системы моделей математики.
В зависимости от состава обучаемых следует акцентировать те или иные приоритеты. Конечно, первый из указанных приоритетов носит универсальный характер и определяет общий вектор перемен. Второй в списке приоритетов предполагает диверсификацию педагогических воздействий в зависимости от характера будущей профессиональной деятельности.
Результаты работы частично апробированы на международных и всероссийских научных конференциях и внедрены в педагогический процесс в Уральском государственном экономическом университете посредством цикла интерактивных электронных учебников, находящихся в свободном доступе, и именных индивидуальных заданий для студентов. Полученные результаты являются основой разрабатываемых нами методик и технологий обучения.
Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 16-06-00240.



